Find the co-ordinates of the point which divides the line segment joining the points (2,3,-4) and (4,-1,2) in the ratio (i) 2 : 3 internally, (ii) 4 : 3 externally.
The correct Answer is:N/a
(i) Let the required point be (x,y,z).
∴x=2×4+3×22+3=145
y=2×(−1)+3×32+3=75
z=2×2+3×(−4)2+3=−85
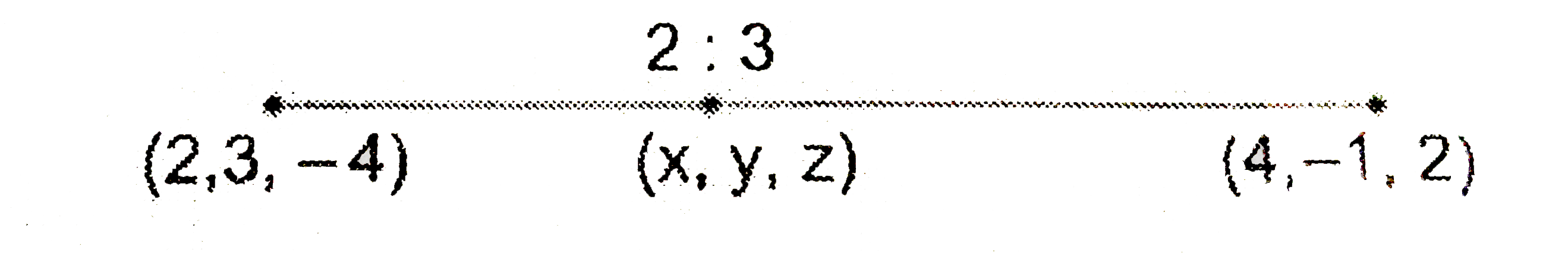
∴ Required point=(145,75,−85).
(ii) Let the required point be (x,y,z).
∴x=4×4−3×24−3=10
y=4×(−1)−3×34−3=−13
z=4×2−3×(−4)4−3=20
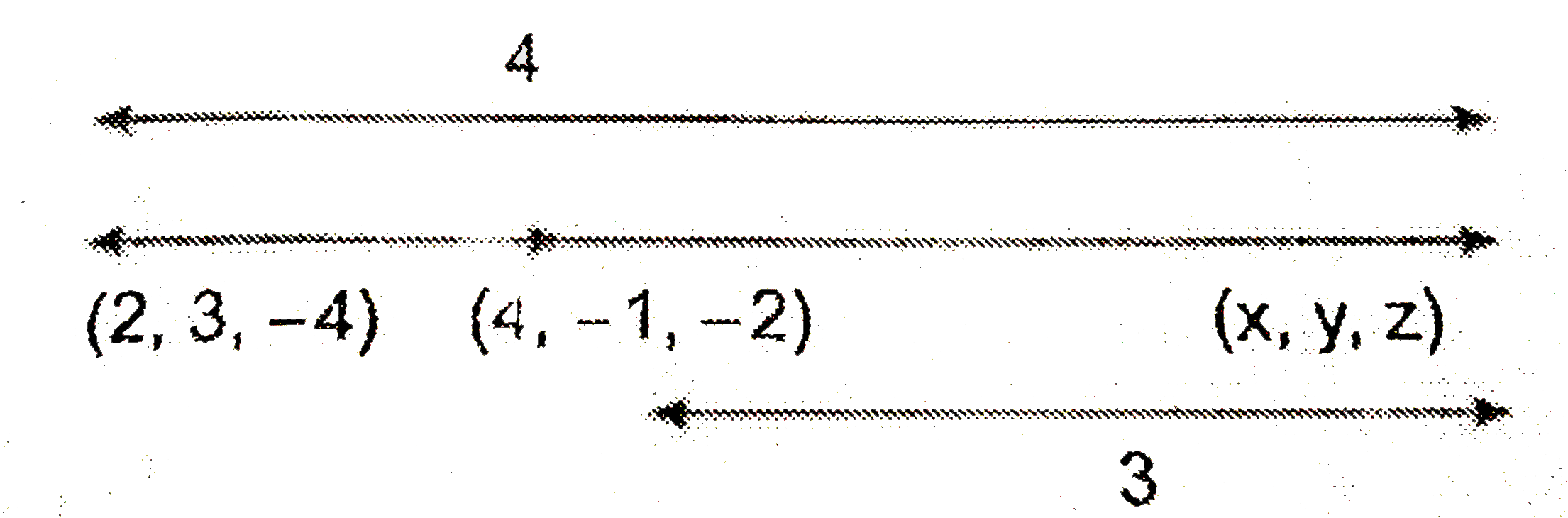
∴ Required point=(10,−13,20)
Topper's Solved these Questions
- INTRODUCTION OF THREE DIMENSIONAL GEOMETRYBook:NAGEEN PRAKASHANChapter:INTRODUCTION OF THREE DIMENSIONAL GEOMETRYExercise:Exercise 12 A
Explore 5 Videos
- INTRODUCTION OF THREE DIMENSIONAL GEOMETRYBook:NAGEEN PRAKASHANChapter:INTRODUCTION OF THREE DIMENSIONAL GEOMETRYExercise:Exercise 12 B
Explore 18 Videos
- CONIC SECTIONBook:NAGEEN PRAKASHANChapter:CONIC SECTIONExercise:Miscellaneous Exercise
Explore 8 Videos
- LIMITS AND DERIVATIVESBook:NAGEEN PRAKASHANChapter:LIMITS AND DERIVATIVESExercise:Miscellaneous Exercise
Explore 30 Videos
Similar Questions
The coordinates of the point which divides the line segment joining the points (5,4,2) and (-1,-2,4) in the ratio of 2:3 externally is
View SolutionFind the co -ordinates of the point which divides the line segment joining the points (5,4,2) and (-1,-2,4) in the ratio
(i) 2:3
(ii) -2:3
View SolutionFind the co-ordinates of a point which divides the line segment joining the points (5, 1) and (-10, 11) in the ratio 2 : 3 internally.
View SolutionFind the co-ordinates of the point which divides the line joining the points (2,-4,3) and (-4,5,-6) in the ratio 2:1
View SolutionFind the coordinates of the point which divides the line segment joining the points A(4, -3) and B(9, 7) in the ratio: 3:2.
View SolutionFind the co-ordinates of the point which divides the line segment joining the points (4,-3) and (8,5) in the ratio 1:3 internally
View SolutionFind the coordinates of the point which divides the line segment joining the points (1,2,3)and (3,4,5)in the ratio 2:3
(i) internally, and (ii) externally.
View SolutionFind the coordinates of the point which divides the line segment joining the points (1, 5, 3) and
(-2, 3, 4) in the ration 3:4 (i) internally, and (ii) externally.
View SolutionFind the coordinates of the point which divides the line segment joining the points (1,−2,3) and (3,4,−5) in the ratio 2:3 (1) internally, and (2)externally
View SolutionFind the coordinates of the points which divides the line segment joining the points (6, 3) and (−4, 5) in the ratio 3 :2 internally.
View Solution
