An object is 5 m to the left of a flat screen. A converging lens for which the focal length is 0.8m is placed between object and screen.
Show that for two positions of lens form images on the screen and determine how far these positions are from the object?
Using the lens formula 1v−1u=1F
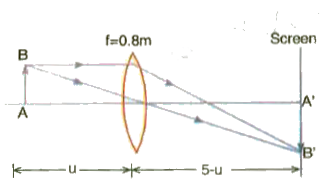
we have 15−u+1u=10.8or15−u+1u=1.25
∴u+5−u=1.25u(5−u)or1.25u2−6.25u+5=0
u= 4m and 1m
Both the values are real, which means there exist two positions of lens that form images of object on the screen.
Topper's Solved these Questions
- RAY OPTICSBOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-I)
37 Videos
- RAY OPTICSBOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-II)
50 Videos
- PRACTICAL PHYSICSBOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions
6 Videos
- SEMICONDUCTOR DEVICESBOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE - II
31 Videos
Similar Questions
An object is 5.0m to the left of a flat screen. A converging lens for which the focal length is f=0.8m is placed between object and screen.
(a) Show that two lens positions exist that form images on the screen and deremine how far these positions are from the object?
(b) How do the two images differ from each other?
View SolutionAn object is 5.0m to the left of a flat screen. A converging lens for which the focal length is f=0.8m is placed between object and screen.
(a) Show that two lens positions exist that form images on the screen and deremine how far these positions are from the object?
(b) How do the two images differ from each other?
View Solution
Knowledge Check
A luminous object and a screen are at a fixed distance D apart. A converging lens of focal length f is placed between the object and screen. A real image of the object in formed on the screen for two lens positins if they are separated by a distance d equal to
A√D(D+4F)B√D(D−4F)C√2D(D−4F)D√D2+4FScreen is placed at a distance 60 cm from an object. A convex lens of focal length f is placed between object and screen and it is attempted that real image of object is formed on the screen. But real image could not be formed for any position of lens between object and screen.
Af must be less than 15 cm.Bf must be greater than 15 cm.Cf must be less than 10 cmDf must be less than 5 cmAn object and a screen are fixed at a distance d apart. When a lens of focal length f is moved between the object and the screen, sharp images of the object are formed on the screen for two positions of the lens.
The magnifications produced at these two positions are M1andM2-Ad gt 2fBdgt4fCM1,M2=1D|M1|−|M2|=1
A luminous object and a screen are at a fixed distance D apart. A converging lens of focal length f is placed between the object and screen. A real image of the object in formed on the screen for two lens positins if they are separated by a distance d equal to
View SolutionA converging lens of focal length 5 cm is placed at a distance of 20 cm from a screen. How far from the lens should an object be placed so as to form its real image on the screen?
View SolutionAn object is placed at a certain distance from a screen. A convex lens of focal length 20cm is placed between the screen and the object. A real image is formed on the screen for two positions of the lens, which differ by a distance of 10cm. What is the distance of the object from the screen ?
View SolutionAn illuminated object is placed at a distance of 20 cm from a converging lens of focal length 15 cm. The image obtained on the screen is:
View SolutionAn object and a screen are fixed at a distance d apart. When a lens of focal length f is moved between the object and the screen, sharp images of the object are formed on the screen for two positions of the lens.
The magnifications produced at these two positions are M1andM2-
View Solution

