If there are two points A and B on rectangular hyperbola xy=c2 such that abscissa of A =ordinate of B, then the locus of points of intersection of tangents at A and B is
Step by step video solution for If there are two points A and B on rectangular hyperbola xy=c^(2) such that abscissa of A =ordinate of B, then the locus of points of intersection of tangents at A and B is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HYPERBOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - HYPERBOLAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
17 Videos
- HYPERBOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - HYPERBOLAEXERCISE - Hyperbola Exercise 11 : Questions Asked in Previous 13 Years Exams
3 Videos
- HYPERBOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - HYPERBOLAEXERCISE - Exercise (Subjective Type Questions)
7 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
10 Videos
- INDEFINITE INTEGRAL BOOK - ARIHANT MATHS ENGLISHCHAPTER - INDEFINITE INTEGRAL EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
Similar Questions
Find the locus of a point P(α,β) moving under the condition that the line y=ax+β is a tangent to the hyperbola x2a2−y2b2=1.
View SolutionMatching the information given in the three columns of the following table column 1, 2 and 3 contain conics, equations of tangents in the conics and points of contact, respectively.
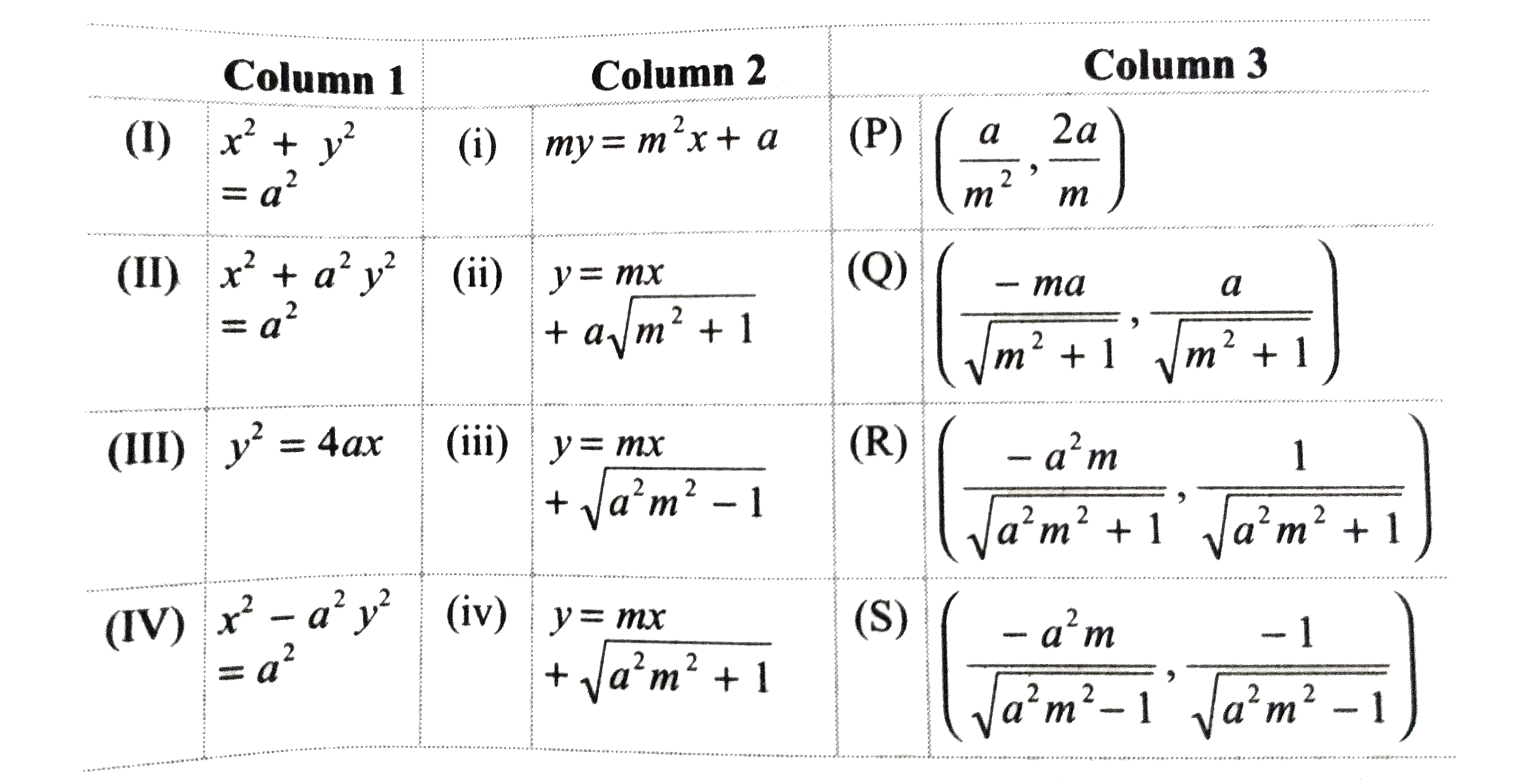
Q. The tangent to a suitable conic (column 1) at (√3,12) is found to be √3x+2y=4, then which of the following options is the correct combination?
View SolutionGiven the base of a triangle and the ratio of the tangent of half the base angles .Show that the vertex moves on a hyperbola whose foci are the extremities of a diameter
View SolutionFind the number of solutions of the equation x21−|x−2|=1, graphically.
View SolutionThe integral ∫sec2x(secx+tanx)92dx equals (for some arbitrary constant K). −1(secx+tanx)112{111−17(secx+tanx)2}+K 1(secx+tanx)111{111−17(secx+tanx)2}+K −1(secx+tanx)112{111+17(secx+tanx)2}+K 1(secx+tanx)112{111+17(secx+tanx)2}+K
View SolutionIf the tangents to the parabola y2=4ax intersect the hyperbola x2a2−y2b2=1 at AandB , then find the locus of the point of intersection of the tangents at AandB.
View SolutionA,B,C are three points on the rectangular hyperbola xy=c^(2), The area of the triangle formed by the tangents at A,B and C.
View SolutionIf there are two points A and B on rectangular hyperbola xy=c^(2) such that abscissa of A= ordinate of B, then locusof point of intersection of tangents at A and B is (a) y^(2)-x^(2)=2c^(2)( b) y^(2)-x^(2)=(c^(2))/(2) (c) y=x( d) non of these
View SolutionShow that at any point on the hyperbola xy=c2, the subtangent varies as the abscissa and the subnormal varies as the cube of the ordinate of the point of contact.
View SolutionTwo tangents are drawn to the hyperbola x2a2−y2b2=1 such that product of their slope is c2 . the locus of the point of intersection is
View SolutionLocus of the point of intersection of the tangents at the points with eccentric angles ϕandπ2 on the hyperbola x2a2−y2b2=1 is
View SolutionIf the tangent drawn to the hyperbola 4y2=x2+1 intersect the co-ordinate axes at the distinct points A and B, then the locus of the mid-point of AB is:
View SolutionThe locus of the point of intersection of tangents drawn at the extremities of normal chords to hyperbola xy=c2
View SolutionIf the normals at three points A, B, C on the rectangular hyperbola xy=c2 intersect at a . Point D on the hyperbola, then
View SolutionThe point of intersection of normals to the parabola y2=4x at the points whose ordinates are 4 and 6 is
View Solutionआयताकार अतिपरवलय xy=2 के बिन्दु P पर स्पर्शरेखा निर्देशी अक्षों को A तथा B पर प्रतिच्छेद करती है, तो त्रिभुज OAB का क्षेत्रफल (जहाँ O मूल बिन्दु है) ज्ञात कीजिये ।
View Solution

