αt2=Fv+βx2
Find the dimension formula for [α]and[β] ( here t = time , F = force , v = velocity , x = distance).
The correct Answer is:[β]=M1L4T−3;[α]=M1L2T−1
To find the dimension formulas for (α) and (β) from the equation
αt2=Fv+βx2
we will follow these steps:
Step 1: Identify the dimensions of the variables involved
1. Force (F): The dimension of force is given by:
(F)=(M)(L)(T−2)
where (M) is mass, (L) is length, and (T) is time.
2. Velocity (v): The dimension of velocity is given by:
(v)=(L)(T−1)
3. Time (t): The dimension of time is:
(t)=(T)
4. Distance (x): The dimension of distance is:
(x)=(L)
Step 2: Calculate the dimension of Fv
Now, we calculate the dimension of the product Fv:
(Fv)=(F)⋅(v)=((M)(L)(T−2))⋅((L)(T−1))=(M)(L2)(T−3)
Step 3: Set up the equation for α
From the equation, we have:
αt2=Fv
This implies:
(α)=(Fv)⋅(t2)
Substituting the dimensions we found:
(α)=(M)(L2)(T−3)⋅(T2)=(M)(L2)(T−1)
Step 4: Calculate the dimension of β
Next, we analyze the term βx2:
βx2=Fv
This implies:
(β)=(Fv)⋅(x2)
Substituting the dimensions we found:
(β)=(M)(L2)(T−3)⋅(L2)=(M)(L4)(T−3)
Final Results
Thus, the dimension formulas for α and β are:
(α)=(M)(L2)(T−1)
(β)=(M)(L4)(T−3)
(F)=(M)(L)(T−2)
where (M) is mass, (L) is length, and (T) is time.
(v)=(L)(T−1)
(t)=(T)
(x)=(L)
(Fv)=(F)⋅(v)=((M)(L)(T−2))⋅((L)(T−1))=(M)(L2)(T−3)
αt2=Fv
This implies:
(α)=(Fv)⋅(t2)
Substituting the dimensions we found:
(α)=(M)(L2)(T−3)⋅(T2)=(M)(L2)(T−1)
βx2=Fv
This implies:
(β)=(Fv)⋅(x2)
Substituting the dimensions we found:
(β)=(M)(L2)(T−3)⋅(L2)=(M)(L4)(T−3)
(α)=(M)(L2)(T−1)
(β)=(M)(L4)(T−3)
टॉपर्स ने हल किए ये सवाल
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Single Correct
90 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Multiple Correct
2 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Exercise 1.3
17 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Video
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Video
समान प्रश्न
The equation of a stationary wave is y=2Asin(2πctλ)cos(2πxλ)
Which of the following is wrong?
View SolutionDimensionsal methods provide three major advantages in verification , deviation , and changing the system of units . Any empirical formula that is derived based on this method has to be verified and propportionality constants found by experimental means . The presence or absence of certain factors - non dimensional constants or variables - cannot be identified by this method . So every dimensionally correct relation cannot be taken as perfectly correct.
The time period of oscillation of a drop depends on surface tension σ , density of the liquid ρ , and radius r . The relation is
View SolutionWhich of the following length measurements is most precise and why?
(a) 2.0cm , (b) 2.00cm , ( c ) 2.000cm
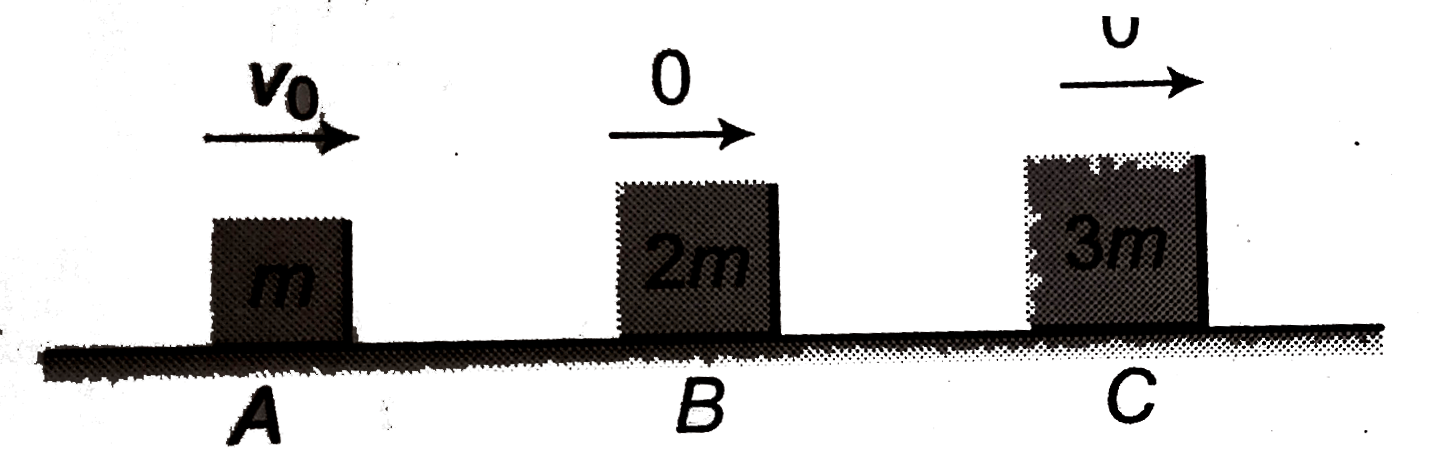
View SolutionThree objects A ,B and C are kept in a straight line on a smooth horizontal surface. These have masses m, 2m and 3m , respectively . The head - on elastic collision takes place between A and B and then B makes completely inelastic collision with C. All motions occur on the same straight line. The final speed of C will be
View SolutionA cyclindrical vessel of height 500 mm has an orifice (small hole) at its bottom. The orifice is initially closed any water is filled in ti upto height H.Now the top is completely sealed with a cap and the orifice at the bottom is opened .Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. The fall in height (in mm) of water level due to opening of the orifice is [ Take atmospheric pressure = 1.0×105Nm2, density of water = 1000kgm3. Neglect any effect of surface tension.]
View Solution(a)/(t^(2)) = Fv = (beta)/(x^(2)) Find dimension formula for [a] and [beta] (here t = "time" ,F = "force", v = "velocity" , x = "distance")
View Solution( alpha)/( t^(2)) = Fv + ( beta)/(x^(2)) Find the dimension formula for [ alpha] and [ beta] ( here t = time , F = force , v = velocity , x = distance).
View SolutionThe function f is given by f=Asinαx+Bcosβt, where x is displacement and t is the time. The dimensions of α/β is
View SolutionIf α=Fv2sinβt, find dimensions of α and β. Here v=velocity, F= force and t= time.
View SolutionThe force of interaction between two atoms is given by F=αβexp(−x2αkt) , where x is the distance ,k is the Boltzmann constant and T is temperature and α and β are two constans. The dimension of β is :
View SolutionFind the dimensions of α/β in equation P=α−t2βx where P= pressure, x is distance and t is time.
View Solutionसमय t व विस्थापन x में संबंध निम्न सूत्र द्वारा व्यक्त है t=α2+βx है यहाॅं पर α व β वह स्थिरांक है| इसमें अवमन्दन होगा (यहाॅं v वेग है)
View SolutionVelocity of a particle at time t is expressed as follows :
v=αt+βt+γ
Dimensions of α,β and γ are respectively.
View Solutionयदि α=Fv2sinβt है α तथा β की विमाऐं ज्ञात करो, जहां v = वेग, F = बल t = समय है।
View SolutionThe force of interaction between two atoms is given by F=αβexp(−x2αkt) , where x is the distance ,k is the Boltzmann constant and T is temperature and α and β are two constans. The dimension of β is :
View Solution

