A 1.5−kg block is initially at rest on a horizontal frictionless surface when a horizontal force in the positive direction of x-axis is applied to the block. The force is given by →F=(4−x2)→iN, where x is in meter and the initial position of the block is x=0.
The maximum kinetic energy of the block between x=0 and x=2.0m is
A.2.33 J
B.8.67 J
C.5.33 J
D.6.67 J
(a) 2.33J
(b) 8.67J
(c) 5.33J
(d) 6.67J
The correct Answer is:C
From work-energy theorem, kinetic energy of the block at
x=xisK=x∫04−x2dx=4x−x33
For K to be minimum, dKdx=0
or 4−x2=0 or x=±2m
At x=+2m, d2Kdx2 is negative, i.e., kinetic energy K is maximum and
Kmax=4×2−(2)33≅5.33J
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Integer
13 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (sinble Correct )
19 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
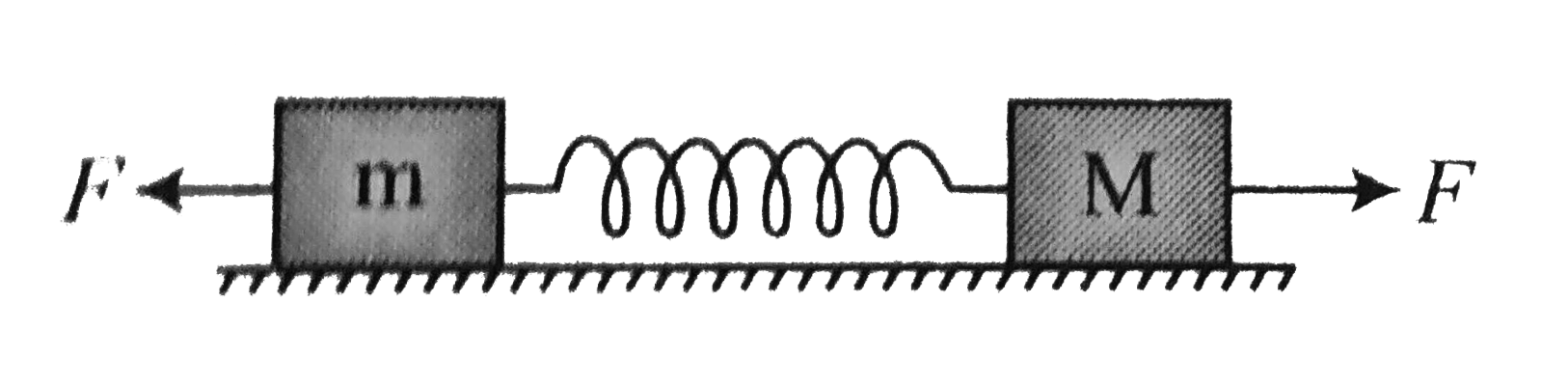
In the situation shown in figure all contact surfaces are smooth. The force constant of the spring is K. Two forces F are applied as shown. The maximum elongation produced in the spring is how many times of F/K (initially the spring is relaxed)?
View SolutionIf machine is lubricated with oil
View SolutionReferring the graphs, which of the following is/are correc?

View SolutionWhich of the following statements is/ are correct(Figure)
View SolutionA 1.5-kg block is initially at rest on a horizontal frictionless surface when a horizontal force in the positive direction of x-axis is applied to the block. The force is given by vecF=(4-x^2)veciN , where x is in meter and the initial position of the block is x=0 . The maximum kinetic energy of the block between x=0 and x=2.0m is
View SolutionA 1.5-kg block is initially at rest on a horizontal frictionless surface when a horizontal force in the positive direction of x-axis is applied to the block. The force is given by vecF=(4-x^2)veciN , where x is in meter and the initial position of the block is x=0 . The maximum positive displacement x is
View SolutionA block of mass 4 kg is initially at rest on a horizontal frixtionless surface. A horizontal force vec(F) = (3+x) hat(i) newtons acts on it, when the block is at x = 0 . The maximum kinetic energy of the block between x = 0 and x = 2 m is
View SolutionA block of mass 4kg is initially at rest on a horizontal frictionless surface. A force →F=(2x+3x2)ˆiN acts horizontally on it. The maximum kinetic energy of the block between x=2m and x=4m in joules is
View SolutionA block of mass 2kg is initially at rest on a horizontal frictionless surface. A horizontal froce ¯¯¯F=(9−x2)¯i newton acts on it, when the block is at x=0. The maximum kinetic energy of the block between x=0m and x=3m in joule is
Conservation of mechanical energ
View SolutionA 1.5kg block is initially at rest on a horizontal frictionless surface. A horizontal force →F=(4−x2)ˆi is applied on the block. Initial position of the block is at x=0. The maximum kinetic enery of the block between x=0 and x=2m is
View SolutionA block is initially at rest on a horizontal frictionless surface when a horizontal force in the positive direction of an axis is applied to the block. The force is given by vecF=(1-x^(2))hatiN , where x is in meters and the initial position of the block is x=0 the maximum kinetic energy of the block is (2)/(n)J in between x=0 ad x=2 m find the value of n .
View SolutionA block of mass m lies on a horizontal frictionless surface and is attached to one end of a horizontal spring (with spring constant k) whose other end is fixed . The block is intinally at rest at the position where the spring is unstretched (x=0). When a constant horizontal force →F in the positive direction of the x−axis is applied to it, a plot of the resulting kinetic energy of the block versus its position x is shown in figure. What is the magnitude of →F ?
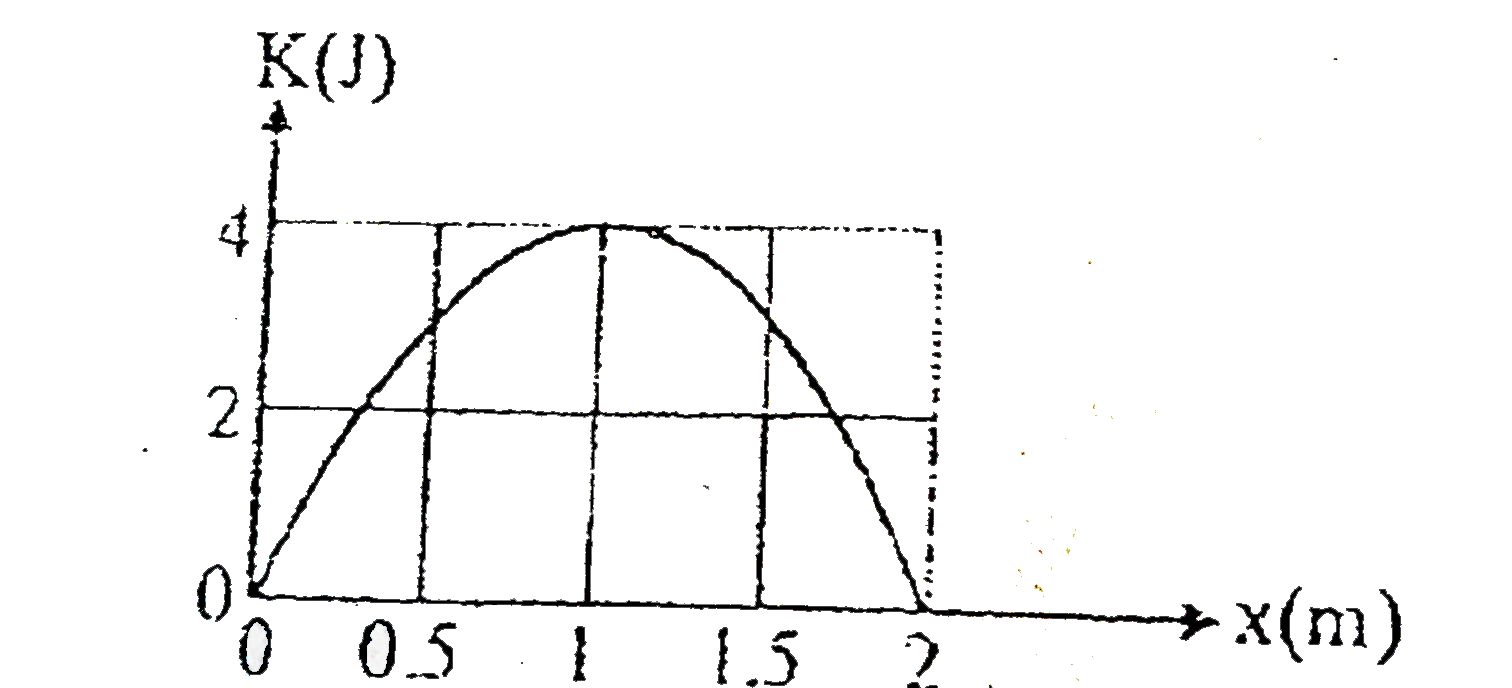
View SolutionA block of mass m lies on a horizontal frictionless surface and is attached to one end of a horizontal spring (with spring constant k) whose other end is fixed . The block is intinally at rest at the position where the spring is unstretched (x=0). When a costant horizontal force →F in the positive direction of the x−axis is applied to it, a plot of the resulting kinetic energy of the block verus its position x is shown in figure. What is the magnitude of →F
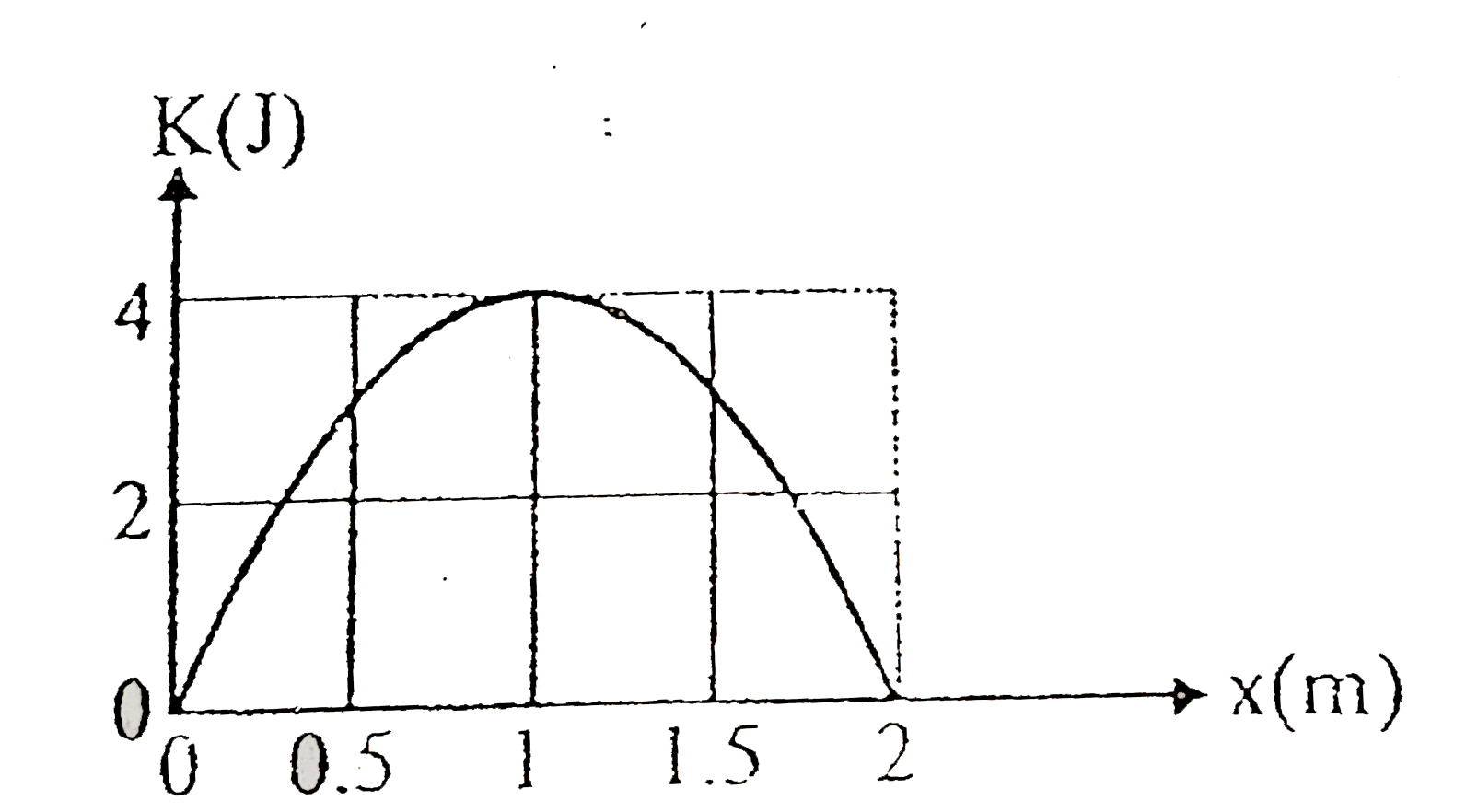
View SolutionA block of mass 1kg is at rest on a horizontal surface at x=0.A force of 6N is applied on block toward positive x -axis.Coefficient of friction between block and surface is variable and depends on the its distance x from origin as mu=((2-x)/(10)) . If v is speed of block at x=2. Find (v^(2))/(1000) .
View SolutionA 1.5 kg block is in a state on a frictionless horizontal plane. A force in the horizontal direction on the block F= (4 - x^2)i Newton is superimposed, where x is in meters. If the initial state of the block is x = 0, then the maximum kinetic energy of the block up to x = 2m will be
View SolutionThe block in Fig. 8-12a lies on a horizontal frictionless surface, and the spring constant is 50 N/m. Initially, the spring is at its relaxed length and the block is stationary at position x=0. Then an applied force with a constant magnitude of 3.0 N pulls the block in the positive direction of the x axis, stretching the spring until the block stops. When that stopping point is reached, what are (a) the position of the block, (b) the work that has been done on the block by the spring force ? During the block's displacement, what are (d) the block's position when its kinetic energy is maximum and (e) the value of that maximum kinetic energy ?
View Solution

