A ball is thrown vertically upwards from the top of a building of height 24.5 m with an initial velocity 19.6 ms−1. Taking g = 9.8 ms, calculate : the velocity with which it will strike the ground .
Given , u = 19.6ms−1 (upwards) , height of building x = 24.5 m .
At the highest point , v = 0
For upward journey , from relation v2=u2−2gh
0=μ2−2gh
or h=u22g=(19.6)22×9.8=19.6m
Topper's Solved these Questions
- LAWS OF MOTIONBook:ICSEChapter:LAWS OF MOTIONExercise:EXERCISE - 3(A)
Explore 19 Videos
- LAWS OF MOTIONBook:ICSEChapter:LAWS OF MOTIONExercise:EXERCISE - 3(A) (Multiple Choice Type)
Explore 2 Videos
- LAWS OF MOTIONBook:ICSEChapter:LAWS OF MOTIONExercise:TOPIC 3 (4 Marks Questions )
Explore 10 Videos
- ICSE ANNUAL EXAMINATION -2020Book:ICSEChapter:ICSE ANNUAL EXAMINATION -2020Exercise:SECTION-II
Explore 45 Videos
- LIGHTBook:ICSEChapter:LIGHTExercise:TOPIC 2 Spherical Mirrors (4 Marks Questions )
Explore 9 Videos
Similar Questions
Explain giving two examples Contact forces .
View SolutionWhich of the following is a contact force :
View SolutionA ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10m s−2 ?, find the initial velocity of the ball
View SolutionThe figure below shows the velocity-time graph of a body moving in a straight line.
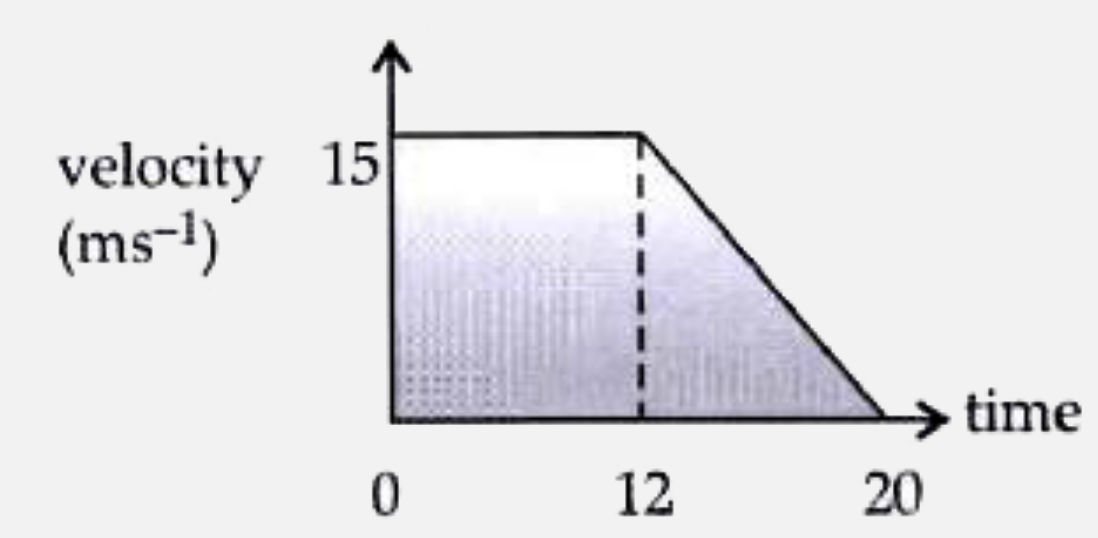
Find the time interval in which the body is moving with zero acceleration
View SolutionDifferentiate between concave mirror and convex mirror.
View SolutionA ball is thrown vertically upwards from the top of tower of height h with velocity v . The ball strikes the ground after time.
View SolutionA ball is thrown vertically upwards with a velocity of 20ms−1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25 m from the ground. How long will it be before the ball hits the ground (Take, g=10ms−2) ?
View SolutionA ball is thrown vertically upwards with the speed of 19.6 ms^(-1) from the top of building and reaches the earth in 6 s. Find the height of the building .
View SolutionA ball is thrown vertically upwards with a velocity of 20ms−1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. (a) How high will the ball rise ? and (b) how long will it be before the ball hits the ground ? Take g=10ms−2.
View SolutionA ball is thrown vertically upwards with a velocity of 20 ms^(-1) from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. (a) How high will the ball rise ? and (b) how long will it be before the ball hits the ground ? Take g = 10 ms^(-2) .
View SolutionA ball is thrown vertically upwards with a velocity of 20ms−1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. (a) How high will the ball rise ? and (b) how long will it be before the ball hits the ground ? Take g=10ms−2.
View SolutionA ball is thrown vertically upwards with a velocity of 20ms−1 from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. (a) How high will the ball rise ? and (b) how long will it be before the ball hits the ground ? Take g=10ms−2.
View SolutionA ball is thrown vertically upwards from the ground with a velocity of 24.5 m/s . If g=9.8 m/s^2 , then the ball will be at a height of 29.4 metres from the ground after time
View SolutionA ball is thrown vertically upwards from the top of a tower with an initial velocity of 19.6m s−1. The ball reaches the ground after 5 s. Calculate the height of the tower . Take g=9.8ms−2 ?
View SolutionA ball is thrown vertically upwards from the top of a tower with an initial velocity of 19.6 "m s"^(-1) . The ball reaches the ground after 5 s. Calculate the velocity of the ball on reaching the ground.Take g= 9.8 "ms"^(-2) ?
View SolutionA ball is thrown vertically upwards. It goes to a height 19.6 m and then comes back to the ground, Find the initial velocity of the ball .
Take g = 9.8 ms−2
View Solution