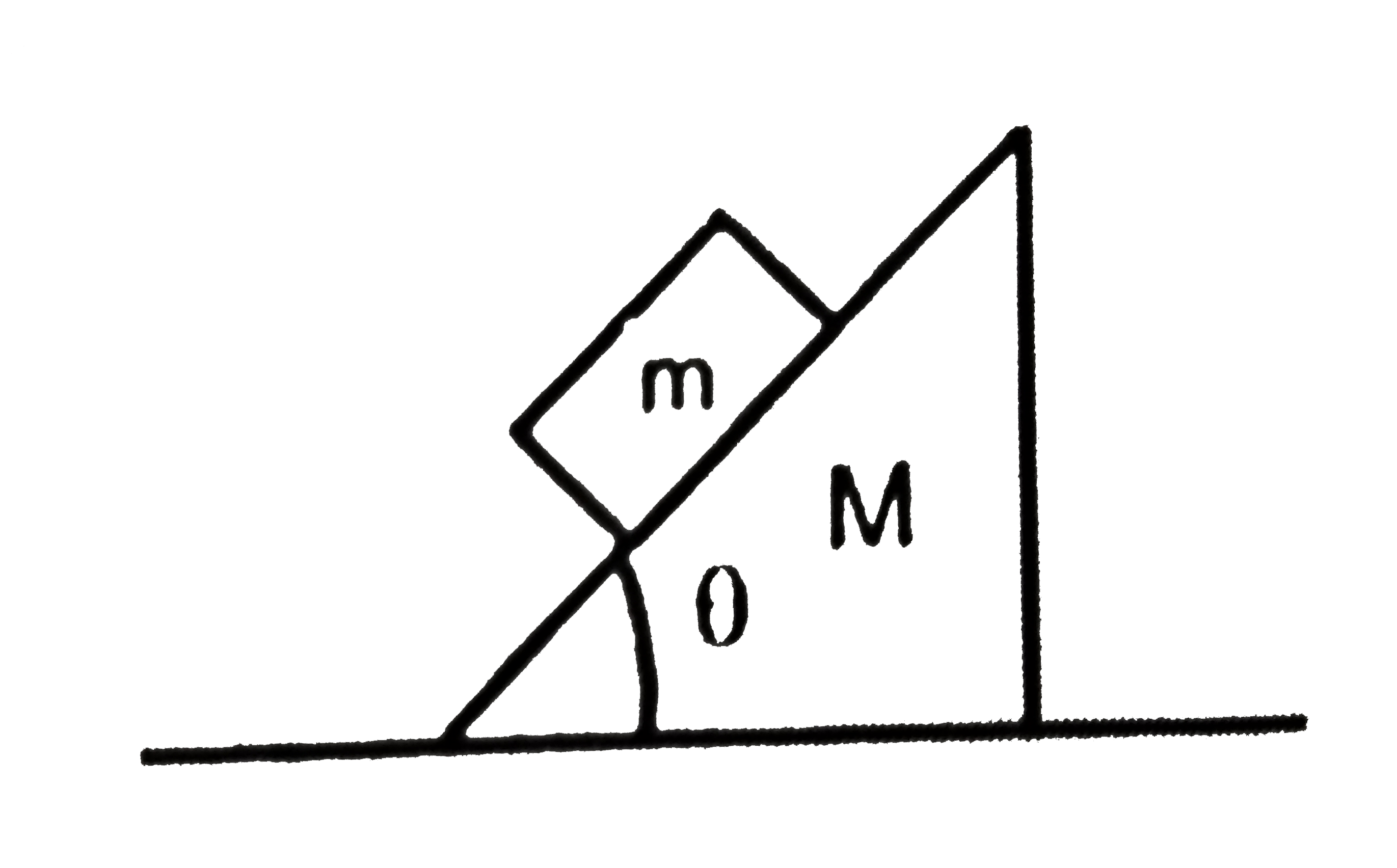
A bar of mass m is placed on a triangular block of mass M as shown in figure The friction coefficient between the two surface is μ and ground is smooth find the minimum and maximum horizontal force F required to be applied on block so that the bar will not slip on the inclined surface of block

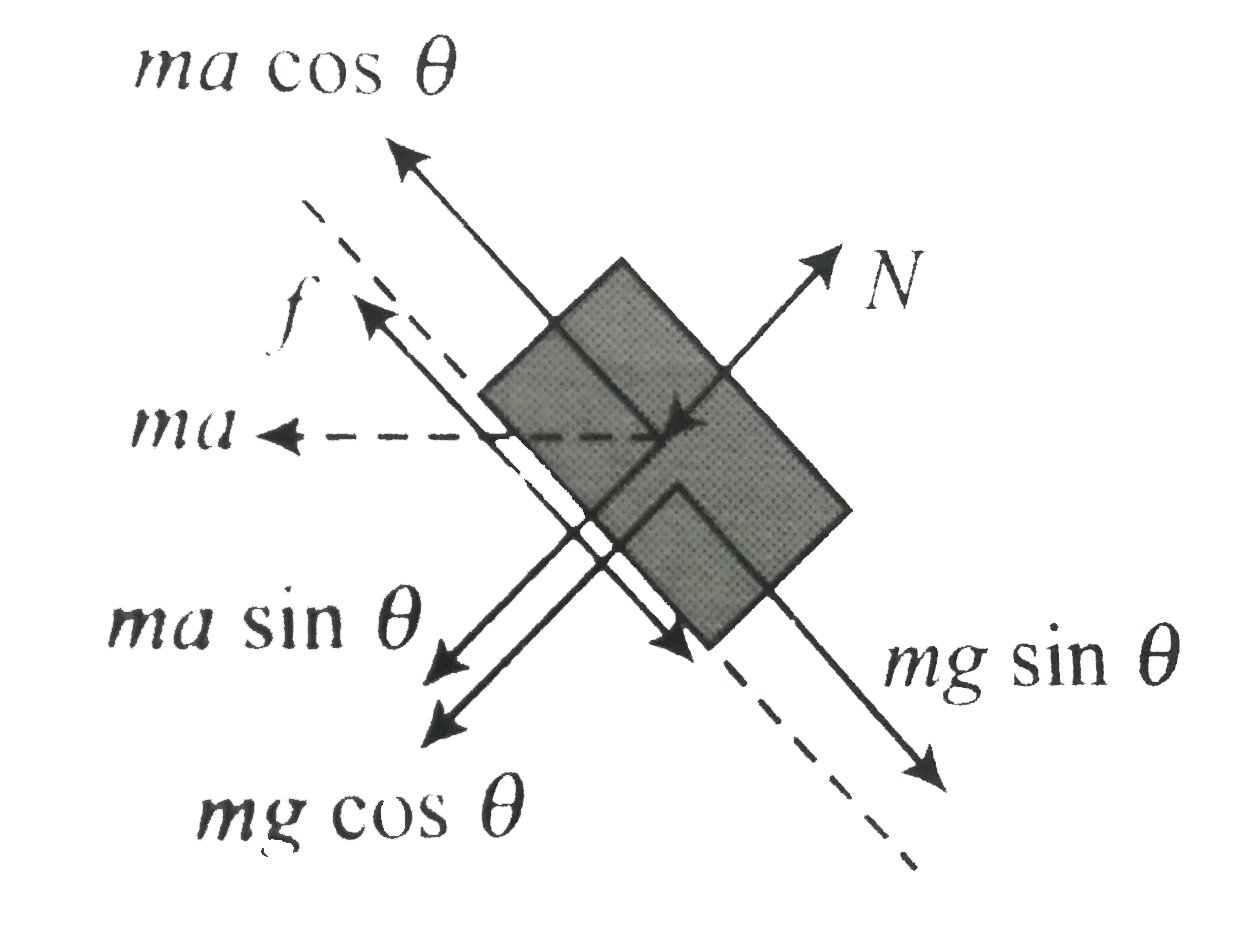
Here if both the masses are moving together , accceleration of the system will be a=F1(M+m) .If we observe the mass m relation to M . It experience a pseudo force out ma toward left . Along the incline it experience two forces mgsinθ downwards and macosθ upward . If mgsinθis morethen macosθwill act in upward direction here if block m is in equlibrium on inclined surface , we most have
f=μN,
Here f=(mgsinθ−macosθ)
and N=(masinθ+mgcosθ)
f=mgsinθ−macosθ≤μ(mgcosθ+masinθ)
or a≥sinθ−μcosθcosθ+μsinθg
or (M+m)a≥sinθ−μcosθcosθ+μsinθ(M+m)g
F≥sinθ−μcosθcosθ+μsinθ(M+m)g....(i)
If force is more than the value obtaional in Eq (i) macosθ will increase on m and the static friction on it will derection At a=gtanθ (when F=(M+m)gtanθ) we know that the force mgsinθ will be balanced by macosθ at this acceleration no friction will act on it , if applied force will increase belond values , macosθ will execed mgsinθ and friction static in downward direction here if block m is in equation we must have f=(macosθ−mgsinθ)N=(mgcosθ+masinθ) and f≤μN
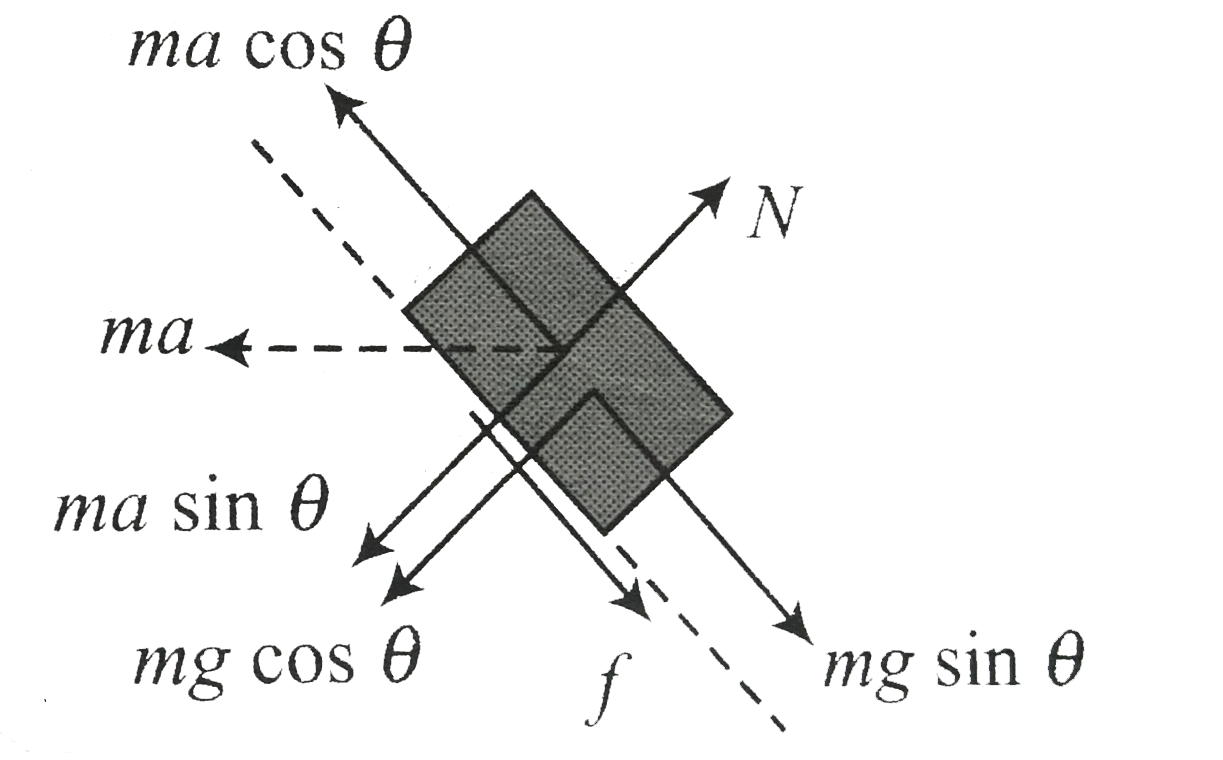
macosθ−mgsinθ≤μ(mgcosθ+masinθ)
⇒a≤sinθ+μcosθcosθ−μsinθg
⇒(M+m)a≤sinθ+μcosθcosθ−μsinθ(M+m)g
⇒F≤sinθ+μcosθcosθ−μsinθ(M+m)g
Hence Fmin≤sinθ−μcosθcosθ+μsinθ(M+m)g
and Fmax≤sinθ+μcosθcosθ−μsinθ(M+m)g
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Solved Examples
Explore 12 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Exercise 7.1
Explore 25 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
A block of mass m is placed on another block of mass M lying on a smooth horizontal surface as shown in the figure. The co-efficient of friction between the blocks is μ. Find the maximum horizontal force F (in Newton) that can be applied to the block M so that the blocks together with same acceleration? (M=3kg,m=2kg,μ=0.1,g=10m/s2)

View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View Solution
Knowledge Check
The coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?
 A0.15mgB0.05mgC0.1mgD0.45mg
A0.15mgB0.05mgC0.1mgD0.45mg
In the adjoining figure, the coefficient of friction between wedge (of mass M) and block (of mass m) is μ.
Find the minimum horizontal force F required to keep the block stationary with respect to wedge.

View SolutionThere are two block as shown in the figure of masses 1kg and 4kg. Friction coefficient between any two surfaces are 0.2 then find maximum value of horizontal force F so that both blocks moves together.
_2019_CBT6_E01_036_Q01.png)
View SolutionA block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it is
View SolutionA block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
View SolutionA block of mass m lies on wedge of mass Mas shown in figure. Find the minimum friction coeffcient required between wedge Mand ground so that it does not move while block m slips down on it.
View SolutionA block of mass m=2kg is resting on a inclined plane of inclination 30∘ as shown in figure The coefficient of friction between the block and the plane is μ=0.5 what minimum force F (in newton) should be applied perpendicular to the plane on the block so that the does not slip on the plane?

View SolutionA block of mass m is pulled by a constant powert P placed on a rough horizontal plane. The friction coefficient the block and surface is μ. The maximum velocity of the block is.
View Solution
