A block is suspended by an ideal spring of force constant force F and if maximum displacement of block from its initial mean position of rest is x0 then
(a) Fk<δ>2Fk
(b) δ=2Fk
(c) Work done by force F is equal to Fδ
(d) Increase in energy stored in the spring is 12kδ2
The correct Answer is:B, C
Let the mass of the block hanging from the spring be m. Then initial elongation of the spring will be equal to mg/k. When the force F is applied to pull the block down, the work done by F and further loss of gravitational potential energy of the block is used to increase strain energy of this spring.
(Fδ+mgδ)=[12k(mgk+δ)2−m2g22k] (i)
From Eq. (i) δ=2F/k
Hence, option (b) is correct.
Since a constant force is applied on the block to pull it down, during this process, work done by force, W=Fδ. Hence, option (c) is also correct.
Increase in energy of the spring is equal to
[12k(mgk+δ)2−m2g22k]
From this equation, increase in energy is not equal to 12kδ2.
Hence, option (d) is wrong.
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Linked Comprehension
Explore 55 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Integer
Explore 13 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Single Correct
Explore 100 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A block of mass m is suspended by different springs of force constant shown in figure.

View SolutionA block of mass m is attached to a frame by a light spring of force constant k. The frame and block are initially at rest with x=x0, the natural length of the spring. If the frame is given a constant horizontal accelration a0 towards left, determine the maximum velocity of the block relative to the frame (block is free to move inside frame). Ignore any friction.
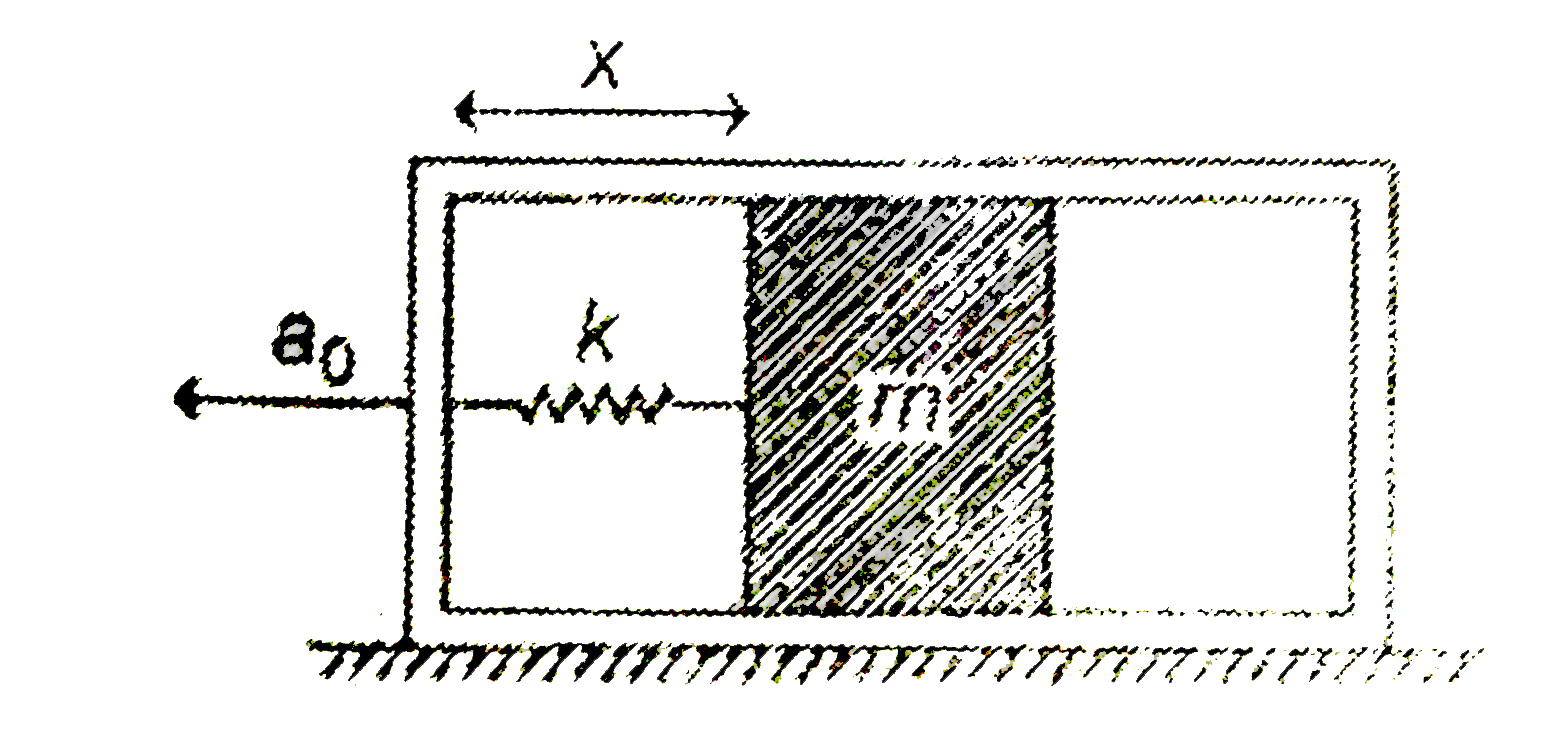
View SolutionA block of mass m attached with a an ideal spring of force constant k is placed on a rough inclined plane having inclination θ with the horizontal and coefficient of friction μ=1/2tanθ, Initially the block is held stationary with the spring in its relaxed state, find the maximum extension in the spring if the block is released.

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA block A of mass m connected with a spring of force constant k is executing SHM. The displacement time equation of the block is x=x0+asinωt. An identical block B moving towards negative x -axis with velocity v0 collides elastically with block A at time t=0. Then
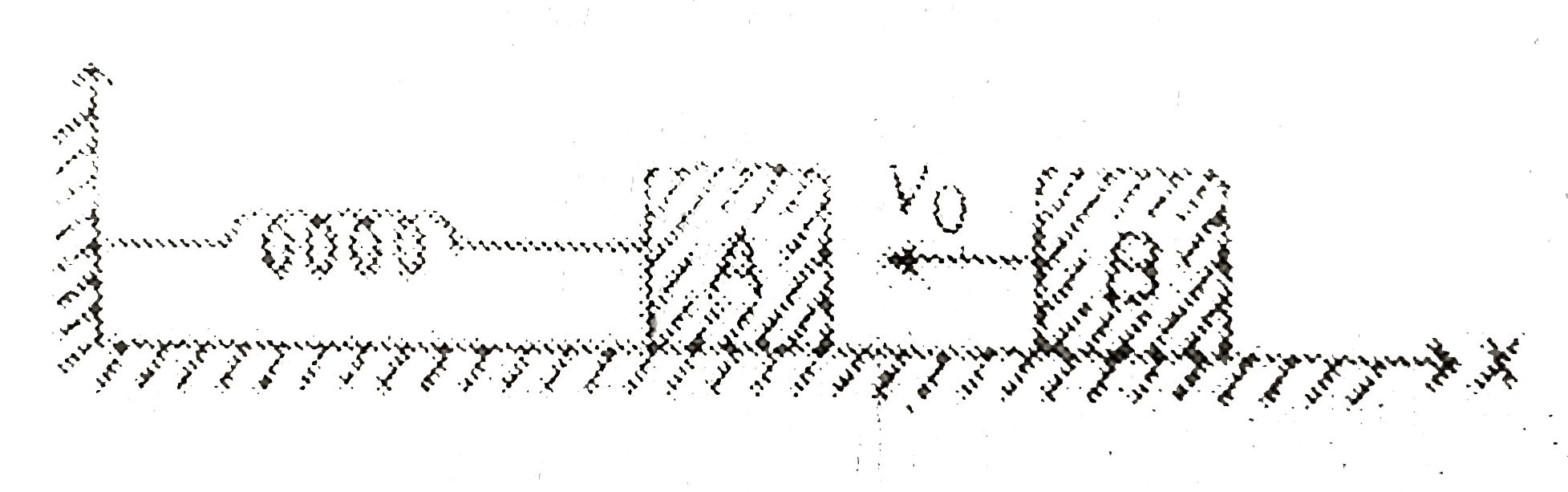
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.

What is acceleration of centre of mass of system at the instant of maximum elongation of spring
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.
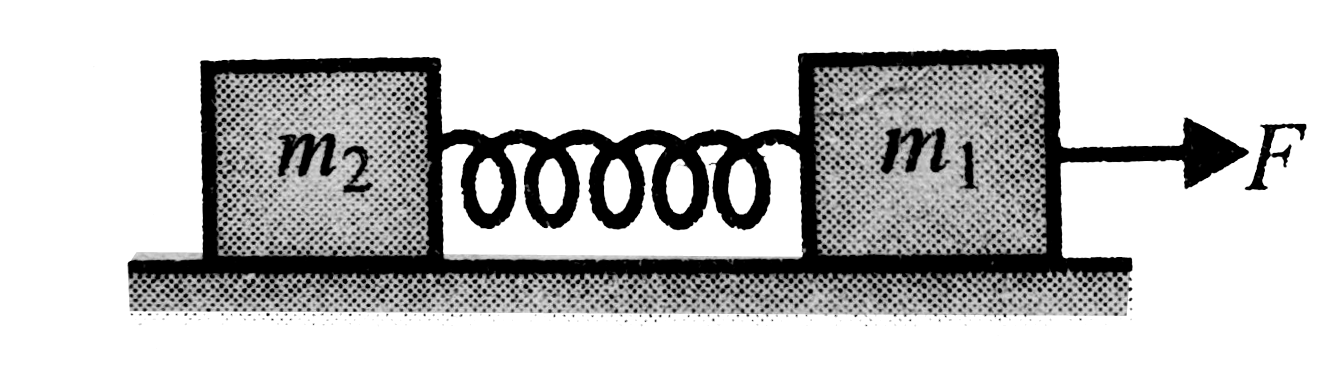
Which of the following statement is not true tn the watt of above system.
View SolutionA block of mass m is suspended through a spring of spring constant k and is in equilibrium. A sharp blow gives the block an initial downward velocity v. How far below the equilibrium position, the block comes to an instantaneous rest?
View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
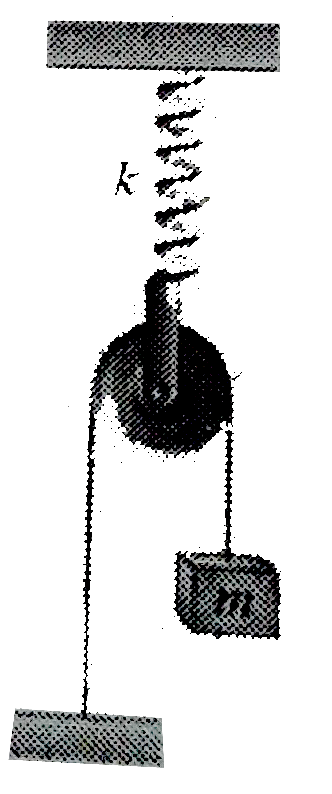
View SolutionA block of mass m=0.1kg is connected to a spring of unknown spring constant k. It is compressed to a distance x from its equilibrium position and released from rest. After approaching half the distance (x2) from the equilibrium position, it hits another block and comes to rest momentarily, while the other block moves with velocity 3ms−1. The total initial energy of the spring is :
View Solution
