A block of mass m=0.1kg is connceted to a spring of unknown spring constant k. It is compressed to a distance x from its equilibrium position and released from rest. After approaching half the distance (x2) from the euilibrium position, it hits another block and comes to rest momentarily, while the other block moves with velocity 3ms−1. The total initial energy of the spring is :
0.3 J
0.6 J
0.8 J
1.5 J
The correct Answer is:C
Conservation of linear momentum
m1u1+m2u2=m1v1+m2v2
m1u+m2u2=m1v1+m2v2
m1u+m(0)=m1(0)+m(3)
(0.1)u=m(3), …(i)
12(0.1)u2=12m(3)2 …(ii)
Solving equation (i) & (ii) we get , u = 3
12kx2=12k(x2)2+12(0.1)32
⇒ 34kx2=0.9⇒34×12kx2=0.9
Intial energy of spring , 12Kx2=0.6J
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (JEE (Advanced) for IIT Entrance)
Explore 7 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (C. Multiple Choice Questions)
Explore 16 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (B. Multiple Choice Questions)
Explore 46 Videos
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
Similar Questions
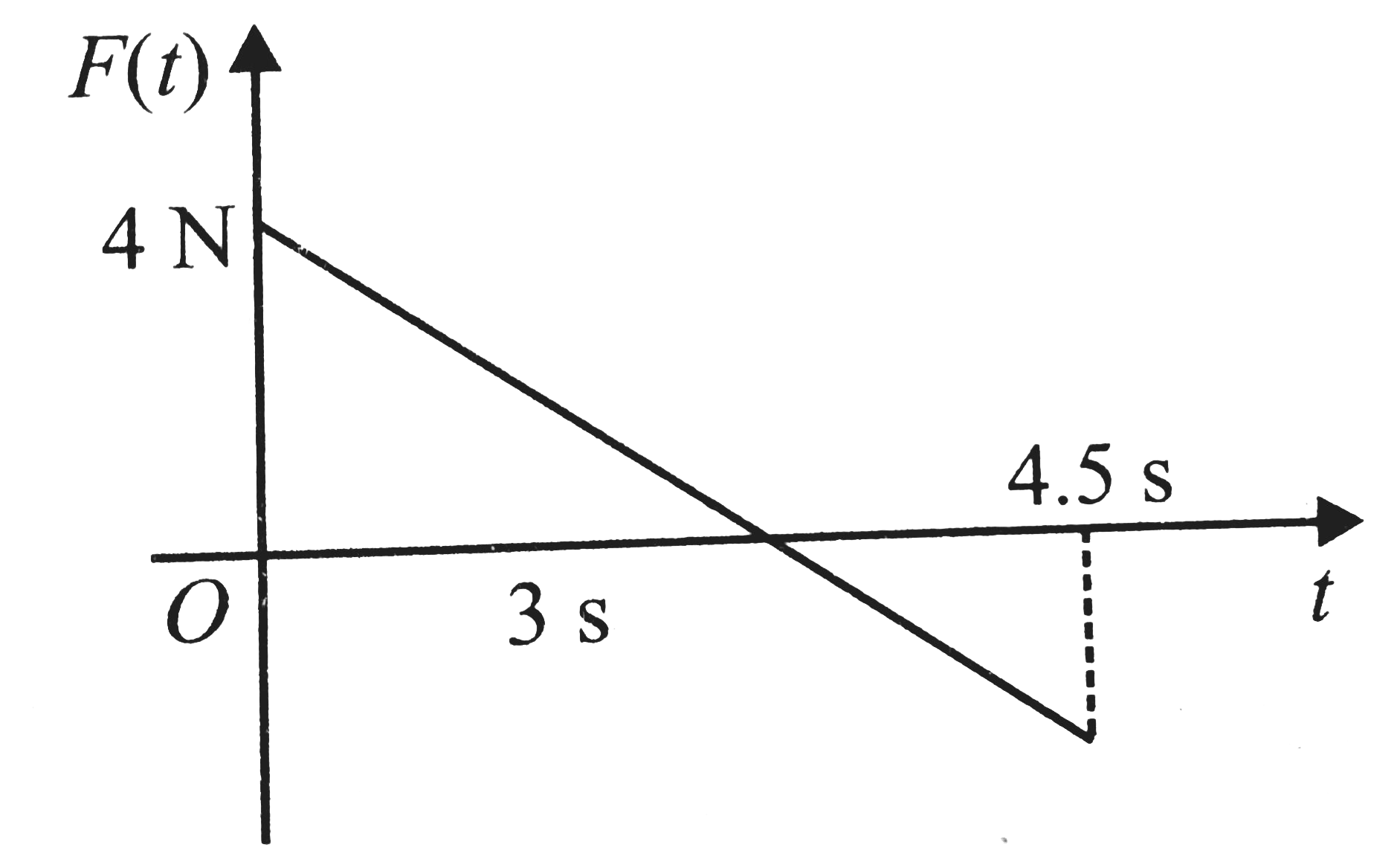
A block of mass 2kg is free to move along the x-axis. It at rest and from t=0onwards it is subjected to a time-dependent force F(t) in the x direction. The force F(t) varies with t as shown in the figure. The kinetic energy of the block after 4.5 seconds is
View SolutionA small particle of mass m moving inside a heavy, hollow and straight tube along the tube axis undergoes elastic collision at two ends. The tube has no friction and it is closed at one end by a flat surface while the other end is fitted with a heavy movable flat piston as shown in figure. When the distance of the piston from closed end is L=L0 the particle speed is v=v0 The piston is moved inward at a very low speed V such that V<<dLLv0, where dL is the infinitesimal displacement of the piston. Which of the following statements(s) is(are) correct?
View SolutionA 25 kg crate starting from rest at the top slides down a plane that makes an angle of 30∘ with the horizontal . Whe it reaches the bottom of the 10 m long slide , its velocity is 8 m/s . The work done by the fore of friction is closest to a value of :
View SolutionWhat is the angle between the particle velocity and wave velocity in longitudinal waves and in transverse ?
View SolutionA block of mass m length force a verical of spring constant k If the block is polled down by a distance of 2mg//k from its equilibrium position and released for the subsequent in the spring to maximum compressed in it mg//k
View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N//m . In the equilibrium position, speed of the block placed horizontally is
View SolutionA block of mass 8 kg is released from the top of an inclined smooth surface as shown in figure. If spring constant of spring is 200 Nm^(-1) and block comes to rest after compressing spring by 1 m then find the distance travelled by block before it comes to rest
View SolutionA block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
View SolutionA block of mass sqrt2 kg is released from the top of an inclined smooth surface as shown in fighre. If spring constant of spring is 100 N/m and block comes to rest after compressing the spring by 1 m, then the distance travelled by block befor it comes to rest is
View SolutionA block of mass m=0.1 kg is connceted to a spring of unknown spring constant k. It is compressed to a distance x from its equilibrium position and released from rest. After approaching half the distance ((x)/(2)) from the euilibrium position, it hits another block and comes to rest momentarily, while the other block moves with velocity 3ms^(-1) . The total initial energy of the spring is :
View SolutionA block of mass 'm' initially at rest is dropped from a height 'h' into a spring whose constant is k. The maximum distance through which the spring is compressed is :
View SolutionA block whose mass m is 680g is fastened to a spring whose spring constant k is 65N/m. The block is pulled a distance x=11cm from its equilibrium position at x=0 on a frictionless surface and released from rest at t= 0. What is the magnitude a_(m) of the maximum acceleration of the block?
View SolutionA block whose mass m is 680g is fastened to a spring whose spring constant k is 65N/m. The block is pulled a distance x=11cm from its equilibrium position at x=0 on a frictionless surface and released from rest at t= 0.
What is the displacement function x(t) for the spring block system?
View SolutionA block of mass m is suspended through a spring of spring constant k and is in equilibrium. A sharp blow gives the block an initial downward velocity v. How far below the equilibrium position, the block comes to an instantaneous rest?
View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N//m . In the equilibrium position, speed of the block placed horizontally is
View SolutionA block of mass 8 kg is released from the top of an inclined smooth surface as shown in figure. If spring constant of spring is 200 Nm^(-1) and block comes to rest after compressing spring by 1 m then find the distance travelled by block before it comes to rest
View Solution
