A car is moving with uniform speed over a circular bridge of radius R which subtends an angle of 90∘ at its center. Find the minimum posible speed so that the car can cross the bridge without losing the contact any where
To solve the problem of finding the minimum possible speed of a car moving over a circular bridge of radius R that subtends an angle of 90∘ at its center, we can follow these steps:
1. Understand the Geometry of the Problem:
- The circular bridge subtends an angle of 90∘ at the center, which means it is a quarter of a circle.
- The radius of the circular bridge is R.
2. Identify Forces Acting on the Car:
- When the car is at the topmost point of the bridge, the forces acting on it are:
- The gravitational force mg acting downwards.
- The centripetal force required to keep the car moving in a circular path, which is provided by the normal force N and is given by mv2R, acting upwards.
3. Set Up the Condition for Maintaining Contact:
- For the car to maintain contact with the bridge, the gravitational force must be greater than or equal to the centripetal force:
mg≥mv2R
- Here, m is the mass of the car, g is the acceleration due to gravity, and v is the speed of the car.
4. Cancel Mass from Both Sides:
- Since m appears on both sides of the inequality, we can cancel it out:
g≥v2R
5. Rearrange the Inequality:
- Rearranging gives us:
v2≤gR
6. Find the Minimum Speed:
- To find the minimum speed v that allows the car to maintain contact, we take the square root of both sides:
v≤√gR
- Therefore, the minimum possible speed of the car is:
v=√gR
Final Answer:
The minimum possible speed so that the car can cross the bridge without losing contact anywhere is v=√gR.
- The circular bridge subtends an angle of 90∘ at the center, which means it is a quarter of a circle.
- The radius of the circular bridge is R.
- When the car is at the topmost point of the bridge, the forces acting on it are:
- The gravitational force mg acting downwards.
- The centripetal force required to keep the car moving in a circular path, which is provided by the normal force N and is given by mv2R, acting upwards.
- For the car to maintain contact with the bridge, the gravitational force must be greater than or equal to the centripetal force:
mg≥mv2R
- Here, m is the mass of the car, g is the acceleration due to gravity, and v is the speed of the car.
- Since m appears on both sides of the inequality, we can cancel it out:
g≥v2R
- Rearranging gives us:
v2≤gR
- To find the minimum speed v that allows the car to maintain contact, we take the square root of both sides:
v≤√gR
- Therefore, the minimum possible speed of the car is:
v=√gR
The minimum possible speed so that the car can cross the bridge without losing contact anywhere is v=√gR.
टॉपर्स ने हल किए ये सवाल
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective
21 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Single Correct
87 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.2
16 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
समान प्रश्न
A block of mass m=4kg is placed over a rough inclined plane as shown in fig . The coefficient of friction between the block and the plane μ=0.5 A force F=10N is applied on the block at an angle of 30∘. Find the contact force between the block and the plane.
k

View SolutionTwo block of masses M1 and, M2 are connected with a string which passed over a smooth pulley . The mass M1 is placed on a tough inclined plane as shown in figure .The coefficient of friction between and block and the inclined plane is μ what should be the minimum mass M2 so that the block M1 slides upwards?

View SolutionA block of mass 1kg is horizontal thrown with a velocity of 10ms−1 on a stationary long of mass 2kg whose surface has a μ=0.5. Plane rest on friction surface find the time when m1 comes to rest w.r.t. plane

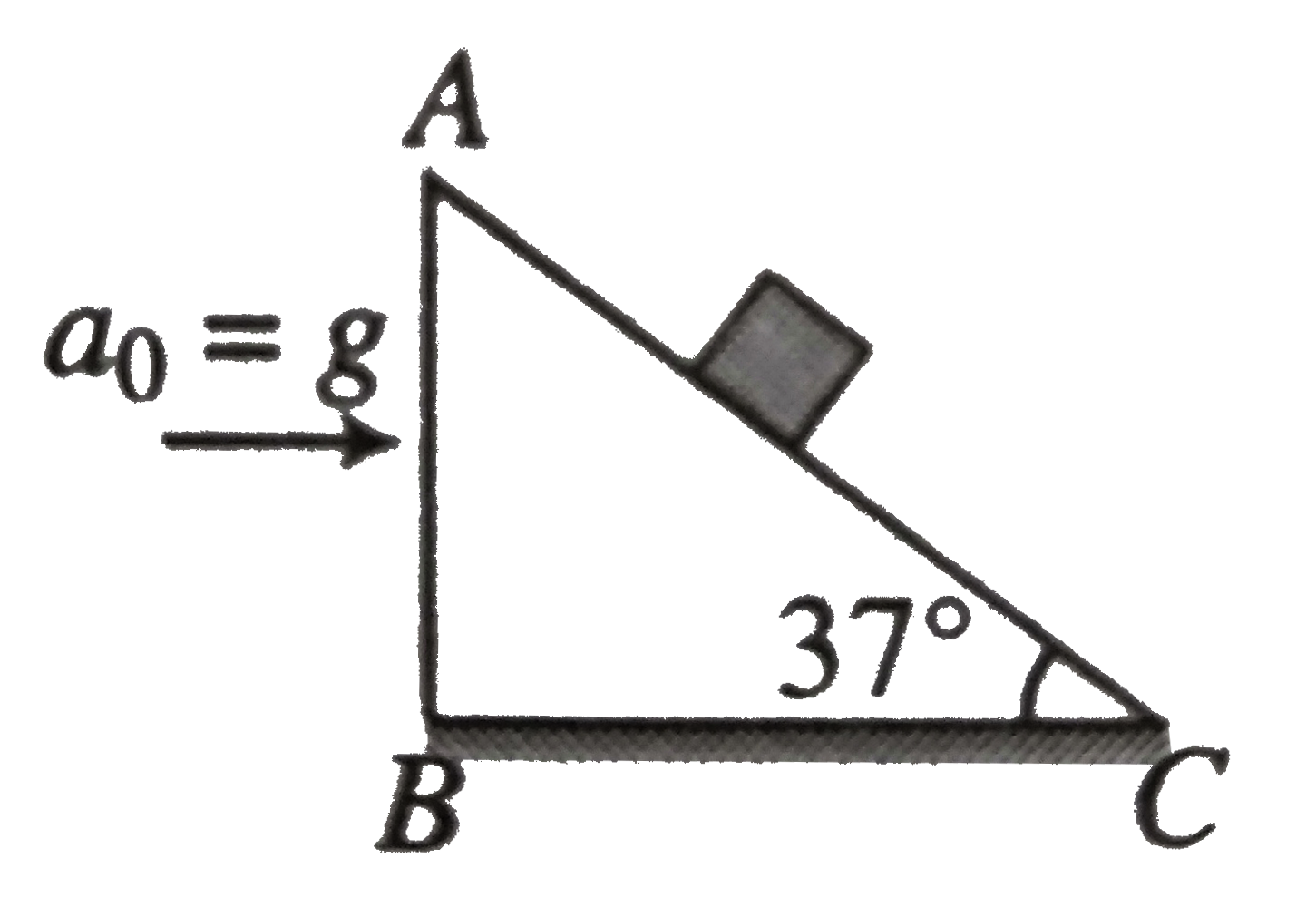
View SolutionA block is placed on an inclined plane moving towards right horizontally with an acceleration a0=g. The length of the plane AC=1m. Friction is absent everywhere. Find the time taken (in seconds) by the block to reach from C to A.
View SolutionTwo soap bubbles A and B are kept in aclosed chamber where the air is maintained at pressure 8Nm2. The radiiof bubbles A and B are 2cm and 4 cm , respectively. Surface tension of the soap-water used to make bubbles is 0.04 N/m. The ratio of nB/nAis ( where nA and nB are the numbe of moles of air in bubbles A and B,respectively.)
[Neglect the effect of gravity]
View SolutionA car of mass m moving over a convex bridge of radius r .Find the normal reaction acting on car when it is at bighest point the bridge.
View SolutionA car of mass m moving over a concave bridge of radius r .Find the normal reaction acting on car when it is at lowest point the bridge
View SolutionA car is moving with uniform speed over a circular bridge of radius R which subtends an angle of 90^(@) at its center. Find the minimum posible speed so that the car can cross the bridge without losing the contact any where
View SolutionThe railway bridge over a canal is in the from of an arc of a circle of radius 20m What is the minimum speed with which a car can cross the bridge without eving contact with the ground at the highest point Take g = 9.8ms^(-2) .
View SolutionA motor car of m travels with a uniform speed v on a convex bridge of radius r. When the car is at the middle point of the bridge, then the force exterted by the car on the bridge is
View SolutionThe roadway bridge over a canal is the form of an arc of a circle of radius 20 m. What is the minimum speed with which a car can cross the bridge without leaving contact with the ground at the highest point (g = 9.8 m/s2
View SolutionA roadway bridge over a rivulet is in the form of quarter of a circle of radius 60 m. What is the maximum speed with which a car can pass over the bridge without leaving the ground at any point ?
View SolutionThe railway bridge over a canal is in the form of an arc of a circle of radius 20m. What is the minimum speed with which a car can cross the bridge without leaving contact with the ground at the highest point ? Take g=9.8ms−2
View SolutionIn the section of a bridge on a river is an arc of a circle of radius 88.2m, then the maximum speed with which a car can travel over the bridge without losing contact with the ground level will be
View SolutionThere is a bridge over the canal in the corner 50 m What is the maximum speed at which a car can cross the bridge without leaving the ground at the highest point of the bridge if it is moving at the maximum speed like the pressure of a circle of radius?
View Solution

