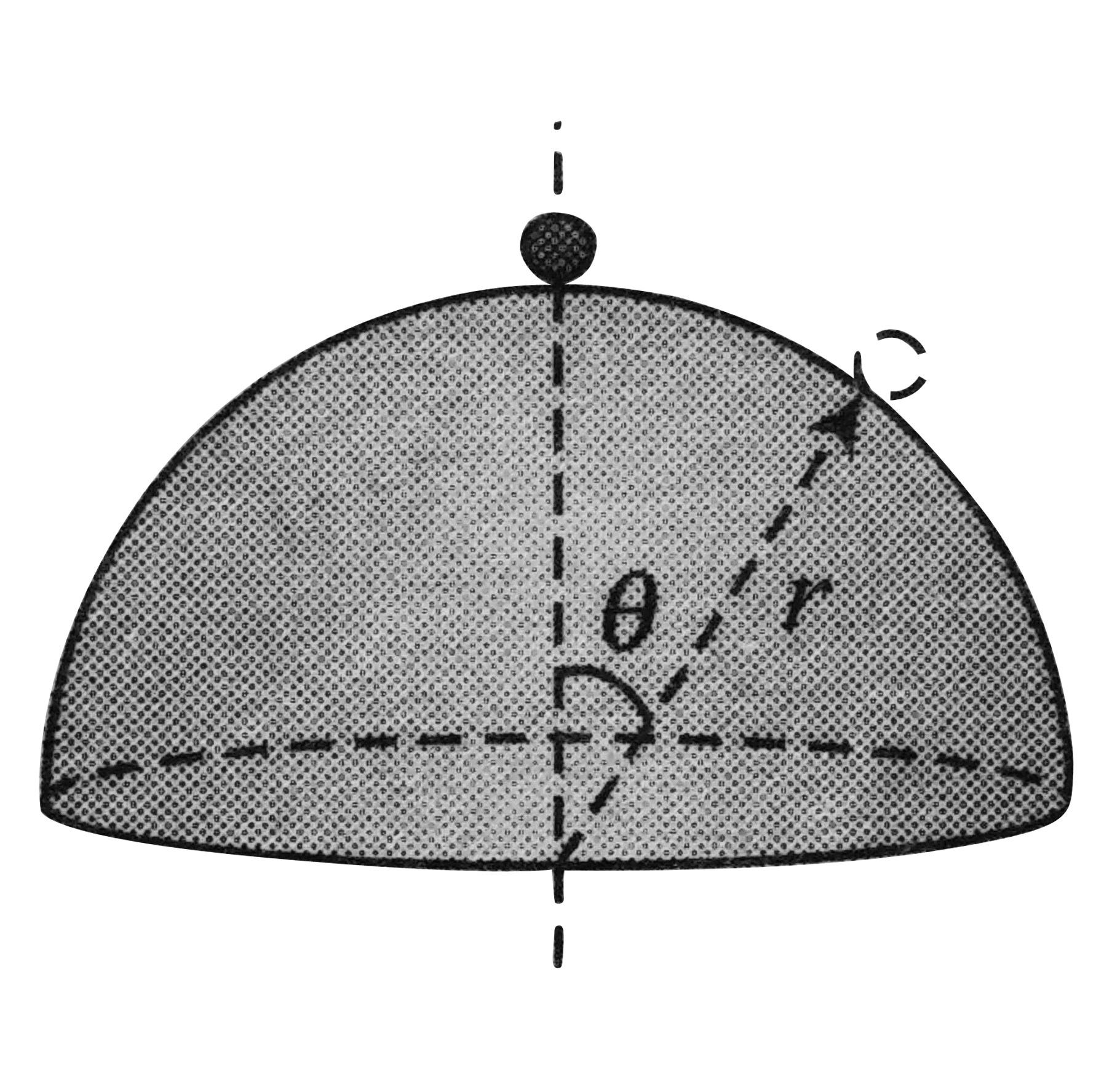
A chain of length l and mass m lies of the surface of a smooth hemisphere of radius R>l with one end tied to the top of the hemisphere. Taking base of the hemisphere as reference line, find the gravitational potential energy of the chain.

(a) mR2gl(lR−sinlR)
(b) mR2g2l(lR−sinlR)
(c) mR2g2l(sinlR−lR)
(d) mR2gl(sinlR−lR)
The correct Answer is:D
The mass of elemental length of chain subtending an angle dthη
at the centre =ml(Rdthη).
∴ Its PE=ml(Rdθ)g[−(R−Rcosθ)]
The negative sign implies that the elemental length is below the datum level. Therefore,
dU=−mgR2l(1−cosθ)dθ
Therefore, total PE of the chain
U=l/R∫0−mgR2l(1−cosθ)dθ
⇒−mgR2l[θ−sinθ]l/R0=−mgR2l[1R−sinlR]

Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Multiple Correct
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Linked Comprehension
Explore 55 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Subjective
Explore 23 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A chain of length l and mass m lies on the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere.
View SolutionA chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration w of each element of the chain when its upper end is released? It is assumed that the length of the chain l<12πR.
View SolutionA particle of mass m initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B.C is centre of the hemisphere. The equation relating θ and θ' is
 .
.
View SolutionA particle of mass m initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B.C is centre of the hemisphere. The equation relating θ and θ' is
 .
.
View SolutionA unifrom flexible chain of length 32 m rests on a fixed smooth sphere of radius R=2π m such that one end A of chain is on the top of the sphere while the other end B is hanging freely. Chain is helpd stationary by a horizontal thread PA as shown . Calculate the acceleration of chain when the horizontal string PA is burnt ( g = 10 m/s2)
View SolutionA small body of mass m slides without friction from the top of a hemisphere of radius r. At what hight will the body be detached from the surface of hemisphere?

View SolutionA chain of length L and mass m is placed upon a smooth surface. The length of BA is (L−b). Calculate the velocity of the chain when its and reaches B

View SolutionA point mass m starts from rest and slides down the surface of a frictionless hemisphere of radius r as shown figure. Measure angle from the vertical and potential energy from the top. Find
a. Find the changes in potential energy of the mass with angle
b. Find the kinetic energy as a function of angle
c. Find the radial and tangential acceleration as a function of angle
d. Find the angle at which the mass files off the hemisphere
e. If there is friction between the mass and hemisphere, does the mass fly off at a greater or lesser angle than in part (d) ?
View SolutionA cylinder of same height and radius is placed on the top of a hemisphere. Find the curved surface area of the shape if the length of the shape by 7cm.
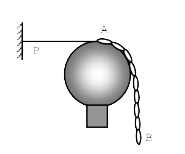
View SolutionA chain of mass per unit length λ and length 1.5 m rests on a fixed smooth sphere of radius R=2πm such that A end of chain is at the top of sphere while the other end is hanging freely. Chain is held stationary by a horizontal thread PA. The tension in the thread is:
View Solution
