A cube is placed so that one corner is at the origin and three edges are along the x-,y-, and ,z-axes of a coordinate system (figure).Use vector to compute
a.The angle between the edge along the z-axis (line ab) and the diagonal from the origin to the opposite corner (line ad).
b. The angle between line ac (the diagonal of a face ) and line ad.
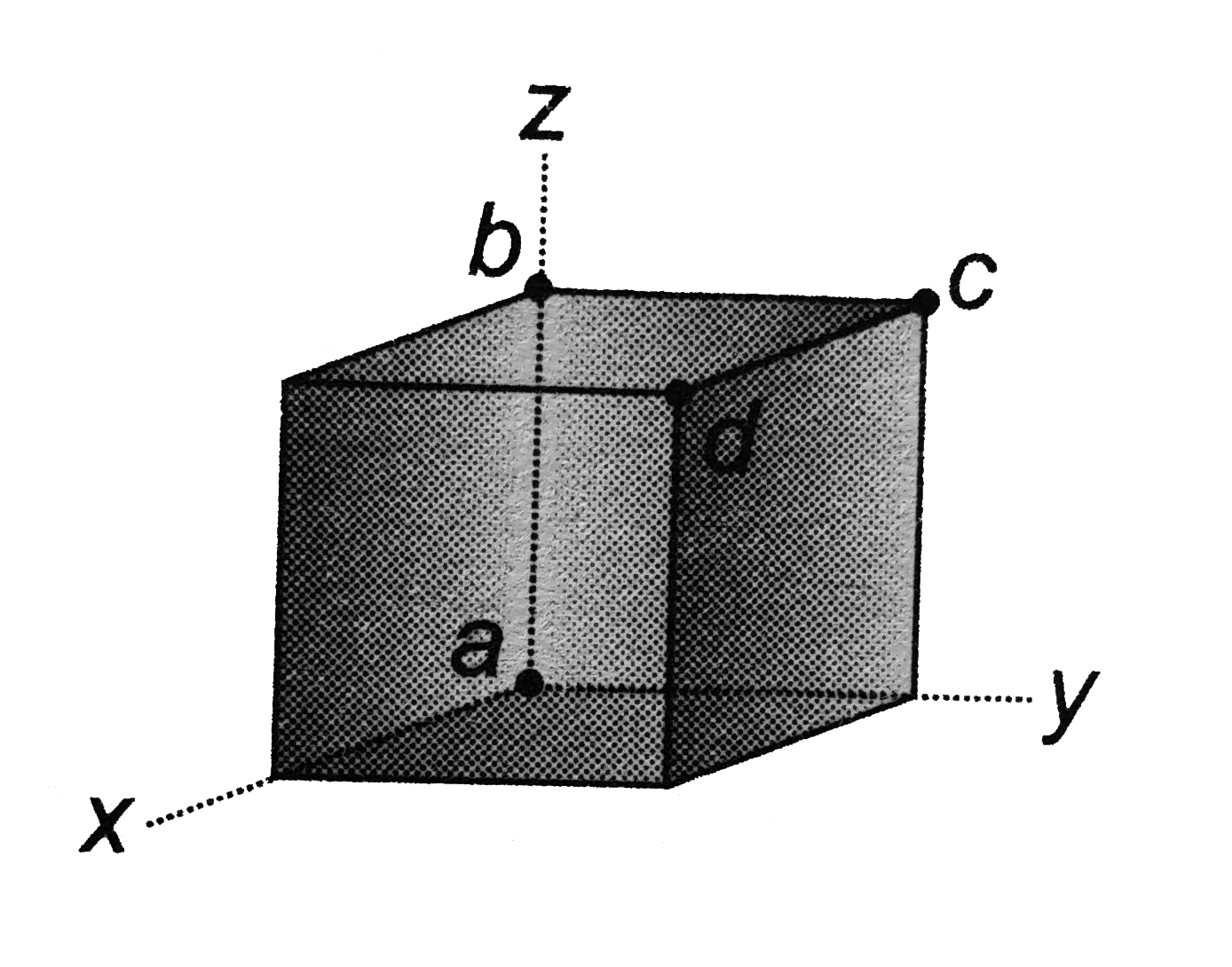
The correct Answer is:a.cos−1(1√3); b. cos^(-1)(sqrt(2)/sqrt(3))
a.Let side of the cube is d,then →ab=dˆk and −→ad=dˆi+dˆj+dˆk
cosθ=→ab.−→ad∣∣∣→ab∣∣∣∣∣∣−→ad∣∣∣=d2d√3d=1√3⇒θ=cos−1(1√3)
→ac=dˆj+dˆk
cosθ=→ac.−→ad∣∣→ac∣∣∣∣∣−→ad∣∣∣=2d2√2d√3d=√2√3
⇒cos−1(√2√2)
Topper's Solved these Questions
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Single Correct
51 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise 3.2
13 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos
Similar Questions
The sum and diffrence of two perpendicular vector of equal length are
View SolutionWhich of the following statements is/ are correct(Figure)
View Solution→A=2ˆi+4ˆj+4ˆk and →B=4ˆi+2ˆj−4ˆk are two vectors. Find the angles between them.
View SolutionThe speed of a transverse wave going on a wire having a length 50 cm and maas 5.0 g is 80ms−1 The area of cross section of the wire is 1.0mm.2 and its Young modulus is 16×1011Nm−2. Find the extension of the wire over its natural lenth.
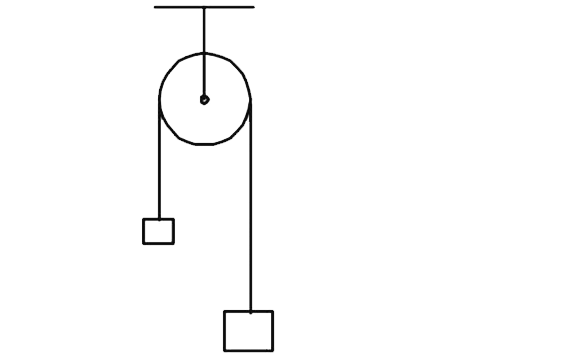
View SolutionA light inextensible string that gas over a smoth fixed polley as shown in the figure connect two blocks of mases it 0.36 kg and 0.72 kg Taking g=10ms−2 , find the work done by the string on the block of mass 0.36 kg doring the first second after the system is released from rest ,
View SolutionA cube is placed so that one corner is at the origin and three edges are along the x-,y-, and ,z-axes of a coordinate system (figure).Use vector to compute
a.The angle between the edge along the z-axis (line ab) and the diagonal from the origin to the opposite corner (line ad).
b. The angle between line ac (the diagonal of a face ) and line ad.

View SolutionFind the angle between the diagonals of a cube with edges of length "a".
View Solutionएक रेखा X,Y तथा Z अक्षो के साथ क्रमश 90∘,135∘,45∘ का कोण बनाती है तो एक रेखा की दिक्-कोज्या ज्ञात कीजिए
View SolutionThe direction rations of the diagonals of a cube which joins the origin to the opposite corner are (when the three concurrent edges of the cube are coordinate axes)
View SolutionIf three vectors along coordinate axis represent the adjacent sides of a cube of length b, then the unit vector along its diagonal passing through the origin will be
View Solutionयदि कोई रेखा x− और y-अक्षों के साथ क्रमशः 30∘ और 60∘ का कोण बनाती है, तो वह रेखा z-अक्ष के साथ कौन-सा कोण बनाएगी ?
View Solutionदिये गये चित्र में घन की प्रत्येक भुजा में 1 ओम का प्रतिरोध जोड़ा गया है। घन के विकर्णतः अभिमुख कोनो के बीच तुल्य प्रतिरोध की गणना कीजिए। यदि इन कोनो के बीच 5 वोल्ट का एक सेल जोड़ दिया जाये, तो सेल से बहने वाली धारा कितनी होगी?
View Solutionएक रेखा x- अक्ष तथा y-अक्ष से क्रमशः 120∘ तथा 60∘ के कोण बनाती है , तो रेखा द्वारा z- अक्ष के साथ बनाया गया कोण ज्ञात कीजिए ।
View SolutionFigure shows a combination of twelve capacitors each of capacitance C forming a cube . Find the equivalent capacitance of the combination ( a) between the diagonally opposite corners A and B of cube ( b) between the diagonally opposite corners A and D of a face of the cube .
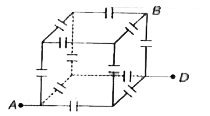
View SolutionThe direction-ratios of the diagonal of a cube, which joins the origin to the opposite corner are (when the 3 concurrent edges of the cube are coordinate axes):
View SolutionIn a cube of edge length a sits with one corncr at the origin of an xyz coordinate system. A body diagonal is a line that extends from one corner to another through the center. In unit-vector , what is the body diagonal that extends from the corner at (a) corrdianates (0,0,0), (b) corrdinates (a,0,0) (c ) coordinates (0,a,0) and (d) coordinates (a,a,0)? (e) Determine the angles that the body diagonals make with the adjacent edges . (f) Determine the length of the boedy diagonals in terms of a.

View Solution

