A cube of side b has a charge q at each of its vertices , Determine the potential and electric field due to this charge array at the centre of the cube.
q/b2
q/2b2
32q/b2
Zero
Step by step video & image solution for A cube of side b has a charge q at each of its vertices , Determine the potential and electric field due to this charge array at the centre of the cube. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A cube of side b has a charge g at each of its vertices. Determine the potential and electric field due to this charge array at the centre of the cube.
View SolutionA cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the center of the cube.
View Solution
Knowledge Check
A hexagon of side 8 cm has a charge 4μC at each of its vertices. The potential at the centre of the hexagon is
A2.7×106VB7.2×1011VC2.5×1012VD3.4×104VA hexagon of side 'a' has a charge 'q' at each of its vertices. The electric field at the centre of hexagon is
A0B14π∈0.qa2C14π∈0.6qa2D14π∈0.6q2a2A cube of side 'a' has point charges +Q located at each of its vertices except at the origin where the charge is -Q. The electric field at the centre of cube is :
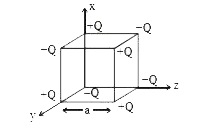 A−Q3√3πε0a2(ˆx+ˆy+ˆz)B−2Q3√3πε0a2(ˆx+ˆy+ˆz)C2Q3√3πε0a2(ˆx+ˆy+ˆz)DQ3√3πε0a2(ˆx+ˆy+ˆz)
A−Q3√3πε0a2(ˆx+ˆy+ˆz)B−2Q3√3πε0a2(ˆx+ˆy+ˆz)C2Q3√3πε0a2(ˆx+ˆy+ˆz)DQ3√3πε0a2(ˆx+ˆy+ˆz)
A regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the centre of the hexagon.
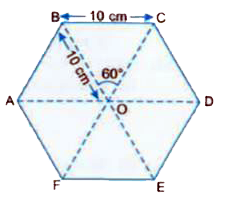
View SolutionTwelve charges have been placed at the centre of each side of a cube as shown in the figure. Find the magnitude of Electric force acting on a charge Q placed at the centre of the cube. Take the side length of the cube to be r.
View SolutionGiven a cube with point charges q on each of its vertices. Calculate the force exerted on any of the charges due to rest of the 7 charges.
View SolutionA cube of side a has a charge q at each of its vertices. The potential energy of the system, of charges is "(Kq^(2))/(a)((12)/(z)+6sqrt(x)+(4)/(sqrt(y)))." Then find "x+y+z".
View SolutionA cube of side L encloses a charge Q at its centre , electric flux through the cube is
View Solution

