A force F acts tangentially at the highest point of a sphere f mass m kept on a rough horizontal plane. If the sphere rolls without slipping, find the acceleration of the centre of the sphere.

The situation is shown fig. As force F rotates the sphere, the point of contact has a tendency to slip towards left so that the static friction on the sphere will act towards right. Let r the radius of the sphere and a be the linear acceleration of the centre of the sphere the angular acceleration about the centre of the spohere is α=ar, as there is no slipping.
For the inear motion of the centre
F+f=ma.............i
and for the rotational motion about the centre,
Fr−=iα=(23mr2)ar
or F−f=25ma.............ii
from eqn i andn ii we get
2F=75ma or a10F7m
Alternative method: As the shre is rolling, we can apply torque equation about point of contact.
i.e. F(2r)=Ipα=(25mr2+mr2)α
⇒F(2r)=(75mr2)α
Hence angular acceleration αs=10F7mr..........iii
As sphere is rolling, acceleration of centre of mass is
a=αr=10F7m
Similar Questions
A force F acts tangentially at the highest point of a sphere of mass m kept on a rough horiozontal plane. If the sphere rolls withut slipping, find the accelerastioni of the centre of the sphere.
View SolutionA force F acts tangentially at the highest point of a solid cylinder of mass m kept on a rough horizontal plane. If the cylinder rolls without slipping, find the acceleration of the center of cylinder.
View Solution
Knowledge Check
A force F acts tangentially at the highest point of a disc of mass m kept on a rough horizontal plane. If the disc rolls without slipping, the acceleration of centre of the disc is:
 A2F3mB10F7mCzeroD4F3m
A2F3mB10F7mCzeroD4F3mA sphere is rolling on a horizontal surface without slipping. The ratio of the rotational K.E. to the total kinetic energy of the sphere is
A25B27C57D37A plane srface is inclined at an angle θ. A cube slides down the plane and a solid sphere rolls down the plane without slipping. The ratio of the acceleration of the cube to that of the sphere is
A1B52C72D27
A tangential force 'F' is applied at the topmost point of a spherical shell of mass 'm' kept on a rough horizontal surface. If it rolls without slipping, it's acceleration is 6Fxm then 'x'
View SolutionA horizontal force F=14N acts at the centre of mass of a sphere of mass m=1kg. If the sphere rolls without sliding, find the frictional force (in N)

View Solution
A tangential force F acts at the top of a thin spherical shell of mass m and radius R. Find the acceleration of the shell if it rolls without slipping.
View SolutionFour identical spheres having mass M and radius R are fixed tightly within a massless ring such that the centres of all spheres lie in the plane of ring. The ring is kept on a rough horizontal table as shown. The string is wrapped around the ring can roll without slipping. The other end of the string is passed over a massless frictionless pulley to a block of mass M. A force F is applied horizontally on the ring, at the same level as the centre, so that the system is in equilibrium.
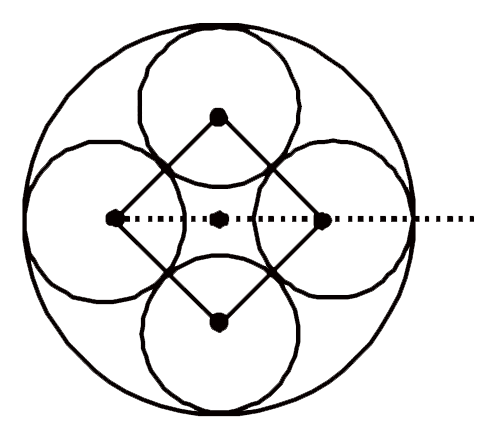
The magnitude of F is
View SolutionFour identical spheres having mass M and radius R are fixed tightly within a massless ring such that the centres of all spheres lie in the plane of ring. The ring is kept on a rough horizontal table as shown. The string is wrapped around the ring can roll without slipping. The other end of the string is passed over a massless frictionless pulley to a block of mass M. A force F is applied horizontally on the ring, at the same level as the centre, so that the system is in equilibrium.
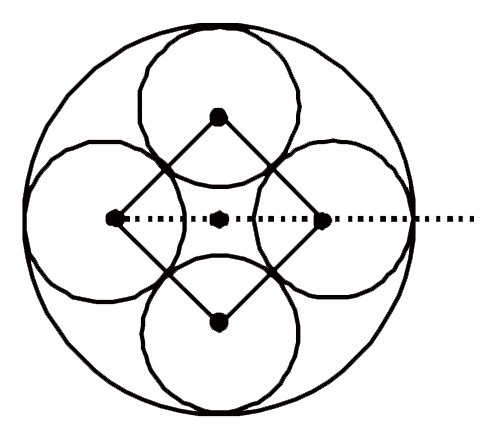
The moment of inertia of the combined ring system about the centre of ring will be
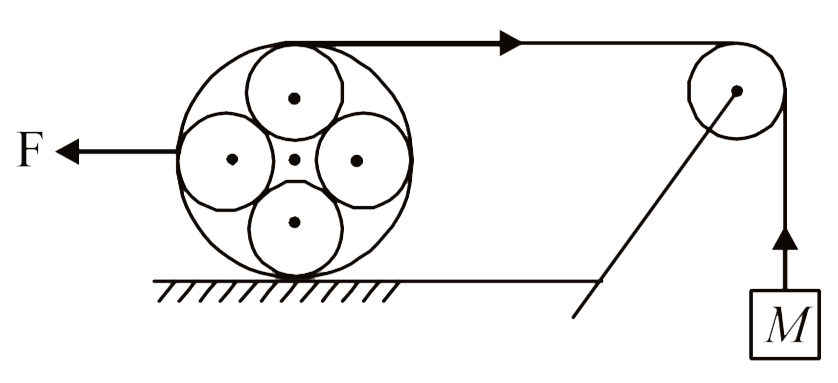
View Solution
