A gaseous mixture enclosed in a vessel consists of one gram mole of a gas A with γ=(53) and some amount of gas B with γ=75 at a temperature T.
The gases A and B do not react with each other and are assumed to be ideal. Find the number of gram moles of the gas B if γ for the gaseous mixture is (1913).
The correct Answer is:B
To solve the problem, we need to find the number of gram moles of gas B in a mixture of gases A and B, given their specific heat ratios (gamma values) and the gamma of the mixture.
1. Identify the Given Values:
- For gas A:
- Number of moles (n1) = 1 mole
- Gamma (γ_A) = 5/3
- For gas B:
- Gamma (γ_B) = 7/5
- For the mixture:
- Gamma (γ_mixture) = 19/13
2. Calculate Cv for Each Gas:
- Using the formula Cv=Rγ−1:
- For gas A:
CvA=R53−1=R23=3R2
- For gas B:
CvB=R75−1=R25=5R2
3. Calculate Cv for the Mixture:
- For the mixture:
Cv_mixture=R1913−1=R613=13R6
4. Apply the Energy Conservation Equation:
- The change in internal energy of the mixture is equal to the sum of the internal energies of gases A and B:
(n1+n2)Cv_mixture=n1CvA+n2CvB
- Substitute the known values:
(1+n2)13R6=1⋅3R2+n2⋅5R2
5. Simplify the Equation:
- Cancel R from both sides:
(1+n2)136=32+n2⋅52
- Multiply through by 6 to eliminate the fraction:
13(1+n2)=9+15n2
- Distributing gives:
13+13n2=9+15n2
6. Rearranging the Equation:
- Move all terms involving n2 to one side:
13−9=15n2−13n2
- This simplifies to:
4=2n2
7. Solve for n2:
n2=42=2
Final Answer:
The number of gram moles of gas B is 2 moles.
- For gas A:
- Number of moles (n1) = 1 mole
- Gamma (γ_A) = 5/3
- For gas B:
- Gamma (γ_B) = 7/5
- For the mixture:
- Gamma (γ_mixture) = 19/13
- Using the formula Cv=Rγ−1:
- For gas A:
CvA=R53−1=R23=3R2
- For gas B:
CvB=R75−1=R25=5R2
- For the mixture:
Cv_mixture=R1913−1=R613=13R6
- The change in internal energy of the mixture is equal to the sum of the internal energies of gases A and B:
(n1+n2)Cv_mixture=n1CvA+n2CvB
- Substitute the known values:
(1+n2)13R6=1⋅3R2+n2⋅5R2
- Cancel R from both sides:
(1+n2)136=32+n2⋅52
- Multiply through by 6 to eliminate the fraction:
13(1+n2)=9+15n2
- Distributing gives:
13+13n2=9+15n2
- Move all terms involving n2 to one side:
13−9=15n2−13n2
- This simplifies to:
4=2n2
n2=42=2
The number of gram moles of gas B is 2 moles.
Topper's Solved these Questions
- LAWS OF THERMODYNAMICSBook:DC PANDEY ENGLISHChapter:LAWS OF THERMODYNAMICSExercise:Exercise 21.1
Explore 1 Video
- LAWS OF THERMODYNAMICSBook:DC PANDEY ENGLISHChapter:LAWS OF THERMODYNAMICSExercise:Exercise 21.2
Explore 7 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEY ENGLISHChapter:LAWS OF THERMODYNAMICSExercise:Example Type 3
Explore 1 Video
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Medical entrances gallery
Explore 39 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:DC PANDEY ENGLISHChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Integer type Questions
Explore 10 Videos
Similar Questions
In a certain chemical process, a lab technician supplies 254 J of heat to a system. At the same time, 73 J of work are done on the system by its surroundings. What is the increase in the internal energy of the system?
View SolutionA gas in a cylinder is held at a constant pressure of 1.7×105Pa and is cooled and compressed from 1.20m3 to 0.8m3. The internal energy of the gas decreases by 1.1×105J.
(a) Find the work done by the gas.
(b) Find the magnitude of the heat flow into or out of the gas and state the direction of heat flow.
(c) Does it matter whether or not the gas is ideal?
View SolutionA cyclic process abcd is given for a monoatomic gas (CV=32R and Cp=52R) as shown in figure. Find Q, W and ΔU in each of the four processes separately. Also find the efficiency of cycle.

View SolutionA rigid ball of mass m strikes a rigid wall at 60∘ and gets reflected without loss of speed as shown in the figure. The value of impulse imparted by the wll on the ball will be
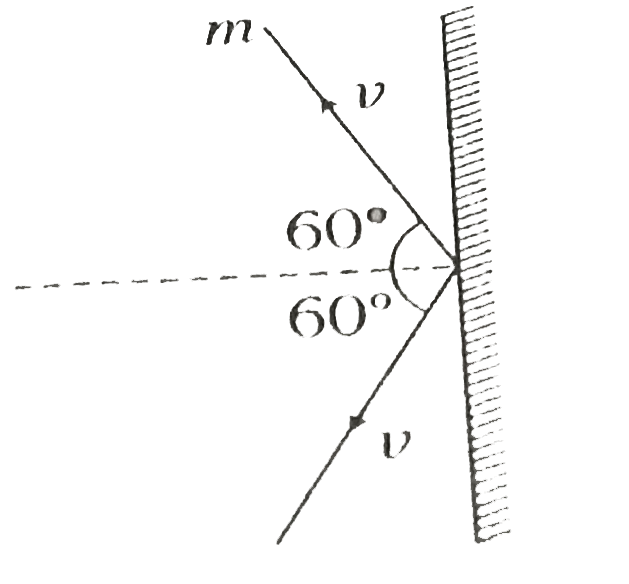
View SolutionTwo parallel, long wires carry currents i1andi2 with i1>i2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 10 μT. If the direction of i2 is reversed, the field becomes 30 μT. Find the ratio i1i2.
View SolutionA gaseous mixture enclosed in a vessel consists of one gram mole of a gas A with γ=(53) and some amount of gas B with γ=75 at a temperature T.
The gases A and B do not react with each other and are assumed to be ideal. Find the number of gram moles of the gas B if γ for the gaseous mixture is (1913).
View SolutionA gaseous mixture enclosed in a vessel of volume V consists of one gram mole of gas A with gamma = (C_(P))/(C_(V)) = (5)/(3) an another gas B with gamma = (7)/(5) at a certain temperature T . The gram molecular weights of the gases A and B are 4 and 32 respectively. The gases A and B do not react with each other and are assumed to be ideal. The gaseous mixture follows the equation PV^(19//13) = constant , in adiabatic process. Find the number of gram moles of the gas B in the gaseous mixture.
View SolutionA gaseous mixture enclosed in a vessel consists of one gram mole of a gas A with γ=(53) and some amount of gas B with γ=75 at a temperature T.
The gases A and B do not react with each other and are assumed to be ideal. Find the number of gram moles of the gas B if γ for the gaseous mixture is (1913).
View SolutionA gaseous mixture enclosed in a vessel consists of one g mole of a gas A with γ=(53) and some amount of gas B with γ=75 at a temperature T . The gases A and B do not react with each other and are assumed to be ideal . Find the number of g moles of the gas B if γ for the gaseous mixture is (1913)
View SolutionA gaseous mixture enclosed in a vessel of volume V consists of one gram mole of a gas LA with gamma=5//3 and another has B with gamma=7//5 at a certain temperature T. The gram molecular weights of the gases A and B are 4 and 32 respectively. The gases A and B do not react with each other and are assumed to be ideal. The gasesous mixture follows the equation PV^(19//13)= constant in adiabatic processes. a. Find the number of gram moles of the gas B in the gaseous mixture. b. Find the speed of sound in the gaseous mixtrue at T=300K . c. If T is raised by 1 K from 300 K, find the percentage change in the speed of sound in the gaseous mixture.
View SolutionA gaseous mixture enclosed in a vessel of volume V consists of one gram mole if a gas ‘A’ with γ=(CpCv)=53 and another gas .B. with γ=75 at a certain of gases A and B are 4 and 32 respectively. The gases do not react with each other and are assumed to be ideal. The gaseous mixture follows the relation PV19/13 = constant in an adiabatic process [519/13=10.5]
Find the number of moles of gas B in the gaseous mixture
View SolutionA gaseous mixture enclosed in a vessel of volume V consists of one gram mole if a gas ‘A’ with γ=(CpCv)=53 and another gas .B. with γ=75 at a certain of gases A and B are 4 and 32 respectively. The gases do not react with each other and are assumed to be ideal. The gaseous mixture follows the relation PV19/13 = constant in an adiabatic process [519/13=10.5]
If T is raised by 1k from 300 k. Find the percentage change in volume.
View SolutionA gaseous mixture enclosed in a vessel of volume V consists of one gram mole if a gas ‘A’ with γ=(CpCv)=53 and another gas .B. with γ=75 at a certain of gases A and B are 4 and 32 respectively. The gases do not react with each other and are assumed to be ideal. The gaseous mixture follows the relation PV19/13 = constant in an adiabatic process [519/13=10.5]
The mixture is compressed adiabatically to 1/5 of its volume. Find the change in its adiabatic compressibility in terms of V and T
View SolutionA gaseous mixture enclosed in a vessel consists of one gram mole of a gas A with γ = 5/3 and another gas B with γ =7/5 at a temperature T. The gases A and B do not react with each other and assumed to be ideal. Find the number of gram moles of the gas B, if γ for the gaseous mixture is (19/13).
View SolutionA gaseous mixture enclosed in a vessel consists of one gram mole of a gas A with gamma=(5/3) and some amount of gas B with gamma=7/5 at a temperature T. The gases A and B do not react with each other and are assumed to be ideal. Find the number of gram moles of the gas B if gamma for the gaseous mixture is (19/13) .
View Solution
