A mass attached to a spring is free to oscillate, with angular velocity ω, in a horizontal plane without friction or damping. It is pulled to a distance x0 and pushed towards the centre with a velocity v0 at time t=0. Determine the amplitude of the resulting oscillations in terms of the parameters omη,x0andv0.
When t=0,x=x0 and dxdt=−v0 ∴ From x=Acos(ωt+θ),x0=Acosθ …(i)
velocity dxdt=−Aωsin(ωt+θ)
−v0=−AωsinθorAsinθ=v0/ω …(ii)
Squaring and adding (i) and (ii), we get
A2(sin2θ+cos2θ)=(v20/ω2)+x20
A=[v20/ω2+x20]1/2
Similar Questions
If amplitude of velocity is V0 then the velocity of simple harmonic oscillator at half of the amplitude is
View SolutionFind the angular frequency and the amplitude of harmonic oscillations of a particle if at distances x1 and x2 from the equalibrium position its velocity equald v1 and v2 respectively.
View Solution
Knowledge Check
A mass attached to a string rotates about a fixed centre with an angular velocity ω in a horizontal plane ,The length of the string and the angular velocity are now doubled .IF T0 is the initial tension in the string , then the new tension will be
A2T0B4T0C8T0D6T0A block of mass m is pushed towards the movable wedge of mass M and height h, with a velocity v0. All surfaces are smooth . The minimum value of v0 for which the block will reach the top of the wedge is
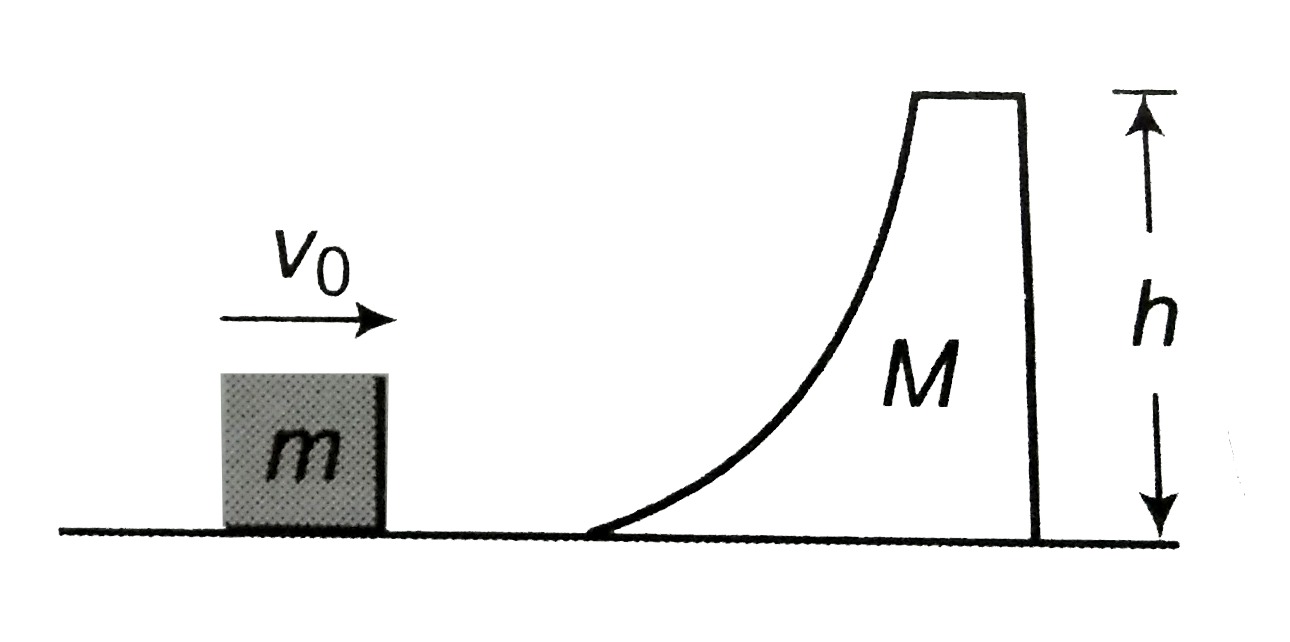 A√2ghB√2ghmMC√2gh(m+M)MD√2ghm(m+M)
A√2ghB√2ghmMC√2gh(m+M)MD√2ghm(m+M)A uniform ring of radius R is given a back spin of angular velocity V0/2R and thrown on a horizontal rough surface with velocity of centre to be V0. The velocity of the centre of the ring when it starts pure rolling will be
AV02BV04C3V04D0
A block of mass 1 kg attached to a spring is made to oscillate with an initial amplitude of 12 cm. After 2 minutes the amplitude decreases to 6 cm. Determine the value of the damping constant for this motion. (take In 2 =0.693 )
View SolutionA mass M attached to a spring of spring constant 0.7 N/m oscillates on a smooth horizontal table. When displacement is 0.3 m, velocity is 2 ms−1. And when displacement is 0.4 m, velocity is 0.3 m/s. Calculate the vlaue of M.
View SolutionA billiard ball of mass m and radius r, when hit in a horizontal direction by a cue at a height h above its centre, acquired a linear velocity v0. The angular velocity ω0 acquired by the ball is
View SolutionOne end of a spring is rigidly fixed. A block attached to the free end of the spring is pulled through a distance x0. On releasing the block, its amplitude of motion cannot exceed ±x0. Why?
View Solution
Consider the situation as shown. If a vehicle moves towards right with constant velocity v0, find the velocity and acceleration of the block in terms of h and x, where x is the distance traveled by the vehicle towards right.
View Solution

