A particle is moving with a velocity of v=(3+6t+9t2)cms. Find out
(a) the acceleration of the particle at t=3s.
(b) the displacement of the particle in the interval t=5s to t=8s.
(a) Velocity of the moving particle v=(3+6t+9t2)
Acceleration of particle, a=dvdt=(6+18t)cm−2
At t = 3 s, a=(6+18×3)cm/s2=60cms−2
(b) Given, velocity v=(3+6t+9t2)cm/s
or dsdt=(3+6t+9t2) or ds=(3+6t+9t2)dt
thereoe By integration ∫s0ds=∫85(3+6t+9t2)dt
The displacement of the particle in the interval t = 5 s to t = 8 s
s=[3t+3t2+3t3]85 or s=1287cm
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.1
10 Videos
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.2
10 Videos
- MOTIONBOOK - DC PANDEYCHAPTER - MOTIONEXERCISE - Medical entrances gallery
19 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
Similar Questions
Which of the following is a one-dimensional motion ?
View SolutionA car moves for half of its time at 80km/h and for rest of time at 40km/h. Total distance covered is 60km. What is the average speed of the car
View SolutionA particle is projected with an angle of projection θ to the horizontal line passing through the points (P,Q) and (Q,P) referred to horizontal and vertical axes (can be treated as X-axis and Y-axis respectively). The angle of projection can be given by
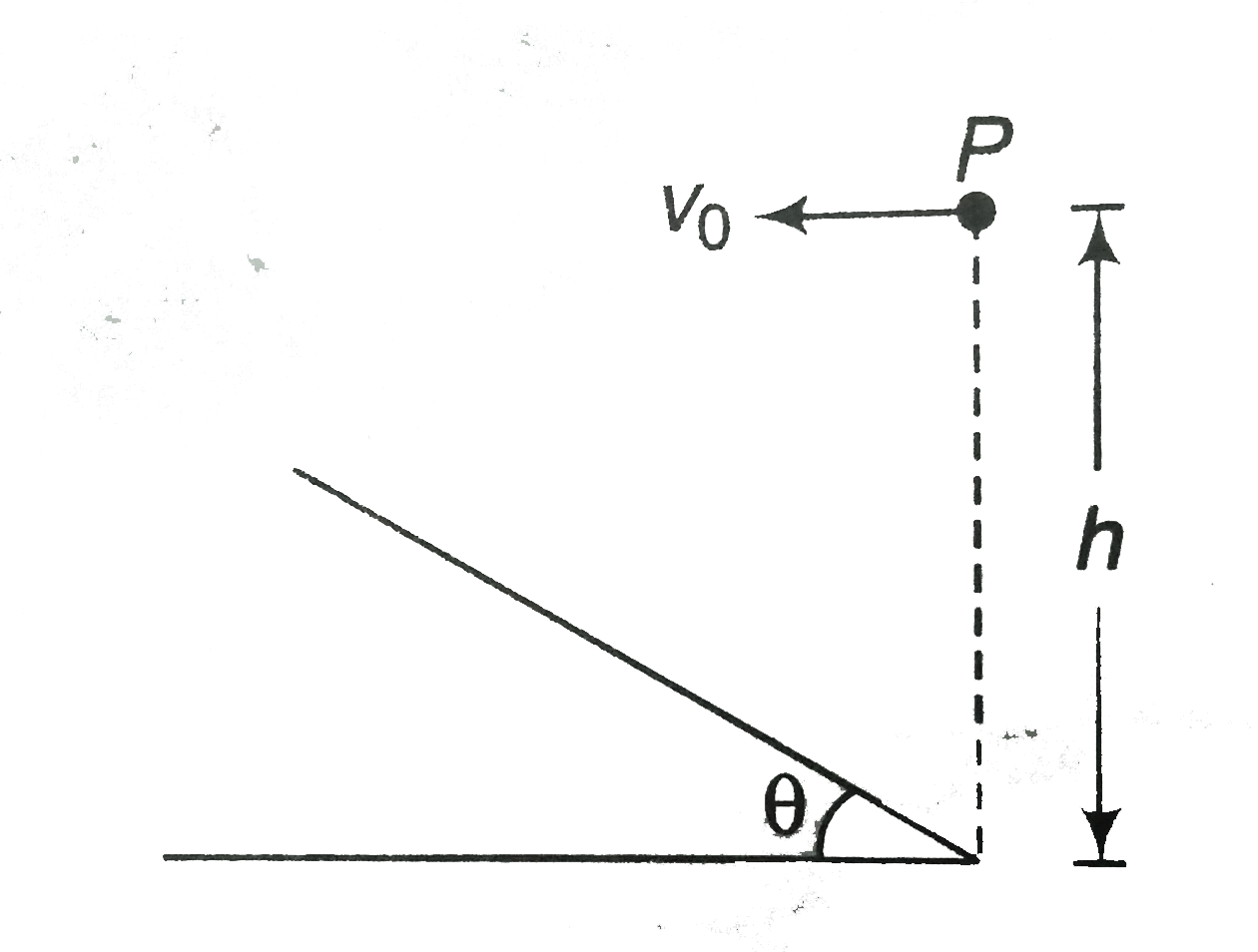
View SolutionDetermine the horizontal velocity v0 with which a stone must be projected horizontally from a point P, so that it may hit the inclined plane perpendicularly. The inclination of the plane with the horizontal is θ and point P is at a height h above the foot of the incline, as shown in the figure.
View SolutionA particle is moving with a velocity of v=(3+ 6t +9t^2) m/s . Find out (a) the acceleration of the particle at t=3 s. (b) the displacement of the particle in the interval t=5s to t=8 s.
View SolutionThe acceleration of particle varies with time as shown.

(a) Find an expression for velocity in terms of t.
(b) Calculate the displacement of the particle in the interval from t=2s to t=4s. Assume that v=0 at t=0.
View SolutionA particle moves along a straight line such that its displacement s at any time t is given by s=t3−6t2+3t+4m, t being is seconds. Find the velocity of the particle when the acceleration is zero.
View SolutionA particle is moving along the x-axis such that s=6t-t^(2) , where s in meters and t is in second. Find the displacement and distance traveled by the particle during time interval t=0 to t=5 s .
View SolutionA particle moves according to law s=t3−6t2+9t+15. Find the velocity when t = 0.
View SolutionIf displacement of particle is s=t3−6t2+9t+15, then velocity of the particle at beginning is
View SolutionThe position of a particle is given by the equation f(t)=t3−6t2+9t where t is measured in second and s in meter. Find the acceleration at time t. What is the acceleration at 4 s?
View SolutionA particle moves along a horizontal line such that its position at any time t is given by s(t)=t3−6t2+9t+1, s in meters and t in seconds.
At what time the particle is at rest?
View SolutionA particle is moving in a striaght line and at a given time, its displacement is S = t^(3) - 6t^(2) + 9t , where t is in seconds and S is in meter . The total distance travelled by the particle during the first five seconds is
View Solutionएक कण v=(3+6t+9t2) सेमी/से के वेग से गतिमान है ज्ञात कीजिए
(a) t = 3 सेकण्ड पर कण का त्वरण |
(b) t = 5 सेकण्ड से t = 8 सेकण्ड के समयान्तराल में कण का विस्थापन।
View SolutionThe acceleration of a particle varies with time t as a=t^(2)+t+2 where t is in seconds. The particle starts with an initial velocity v-3m/s at t=0. find the velocity of the particle at the end of 5s.
View Solutionविरामावस्था (t = 0 पर) से गतिशील किसी कण का विस्थापन s=6t2−t3 द्वारा व्यक्त किया जाता है। वह समय जिस पर कण का वेग पुनः शून्य हो जाये, होगा :
View Solution

