A particle is placed at the lowest point of a smooth wire frame in the shape of a parabola, lying in the vertical xy-plane having equatioin x2=5y(x,y are in meter). After slight displacement, the particle is set free. Find angular frequency of osciallation (in rad/sec) (Take g=10 m/s2)
2 rad/s
4 rad/s
6 rad/s
8 rad/s
The correct Answer is:A
To solve the problem of finding the angular frequency of oscillation of a particle placed at the lowest point of a smooth wire frame in the shape of a parabola, we can follow these steps:
Step 1: Understand the Parabola Equation
The equation of the parabola given is x2=5y. This represents a parabola that opens upwards with its vertex at the origin (0,0).
Step 2: Identify the Lowest Point
The lowest point of the parabola is at the origin (0,0). When the particle is at this point and is slightly displaced, it can oscillate about this point.
Step 3: Determine the Slope of the Parabola
To find the slope of the parabola at any point, we differentiate the equation y=x25:
dydx=2x5
At the lowest point (x = 0), the slope is dydx=0.
Step 4: Analyze Forces Acting on the Particle
When the particle is displaced by a small angle θ, the gravitational force mg acts downwards. The component of this force acting along the slope of the parabola can be expressed as:
F=−mgsin(θ)
For small angles, we can approximate sin(θ)≈θ.
Step 5: Relate the Angle to Displacement
From the slope of the parabola, we have:
tan(θ)=dydx=2x5
For small angles, tan(θ)≈θ, thus:
θ≈2x5
Step 6: Set Up the Equation of Motion
The force acting on the particle can be written as:
F=−mgθ
Substituting θ from the previous step:
F=−mg(2x5)
Using Newton's second law F=ma, where a=d2xdt2:
md2xdt2=−mg(2x5)
Dividing through by m:
d2xdt2=−g(2x5)
Step 7: Substitute the Value of g
Given g=10m/s2:
d2xdt2=−10(2x5)=−4x
Step 8: Identify the Angular Frequency
This equation can be compared to the standard form of simple harmonic motion:
d2xdt2=−ω2x
From our equation, we have:
ω2=4
Thus, the angular frequency ω is:
ω=√4=2rad/s
Final Answer
The angular frequency of oscillation is ω=2rad/s.
---
The equation of the parabola given is x2=5y. This represents a parabola that opens upwards with its vertex at the origin (0,0).
The lowest point of the parabola is at the origin (0,0). When the particle is at this point and is slightly displaced, it can oscillate about this point.
To find the slope of the parabola at any point, we differentiate the equation y=x25:
dydx=2x5
At the lowest point (x = 0), the slope is dydx=0.
When the particle is displaced by a small angle θ, the gravitational force mg acts downwards. The component of this force acting along the slope of the parabola can be expressed as:
F=−mgsin(θ)
For small angles, we can approximate sin(θ)≈θ.
From the slope of the parabola, we have:
tan(θ)=dydx=2x5
For small angles, tan(θ)≈θ, thus:
θ≈2x5
The force acting on the particle can be written as:
F=−mgθ
Substituting θ from the previous step:
F=−mg(2x5)
Using Newton's second law F=ma, where a=d2xdt2:
md2xdt2=−mg(2x5)
Dividing through by m:
d2xdt2=−g(2x5)
Given g=10m/s2:
d2xdt2=−10(2x5)=−4x
This equation can be compared to the standard form of simple harmonic motion:
d2xdt2=−ω2x
From our equation, we have:
ω2=4
Thus, the angular frequency ω is:
ω=√4=2rad/s
The angular frequency of oscillation is ω=2rad/s.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - More than one option is correct
50 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension types
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Only one question is correct
48 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A particle is executing SHM with amplitude A. At displacement x=(−A4), force acting on the particle is F, potential energy of the particle is U, velocity of particle is v and kinetic energy is K. Assuming potential energyh to be zero at mean position. At displacement x=A/2
View SolutionPassage I) In simple harmonic motion force acting on a particle is given as F=−4x, total mechanical energy of the particle is 10 J and amplitude of oscillations is 2m, At time t=0 acceleration of the particle is −16ms2. Mass of the particle is 0.5 kg.
Potential energy of the particle at mean position is
View SolutionA student says that he had applied a force F=−k√x on a particle and the particle performs in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he has worked only with positive x and no other force acted on the particle.
View SolutionWhen an electric field is applied across a semiconductor,
View SolutionIf a machine perform 4000 J output work and 1000 J is inside loss due to friction , then the find efficiency?
View SolutionA particle is projected vertically upwards with an initial velocity of 40 m//s. Find the displacement and distance covered by the particle in 6 s. Take g= 10 m//s^2.
View SolutionThe angular displacement of a particle is given by theta =t^3 + t^2 + t +1 then,the angular acceleration of the particle at t=2 sec is ……. rad s^(-2)
View SolutionA smooth wire frasme is in the shape of a parabola y = 5x^(2) . It is being rotated about y-axis with an angular velocity omega . A small bead of mass (m = 1 kg) is at point P and is in equilibrium with respect to the frame. Then the angular velocity omega is (g = 10 m//s^(2))
View SolutionA particle is placed at the lowest point of a smooth wire frame in the shape of a parabola, lying in the vertical xy-plane having equatioin x^(2) =5y(x,y are in meter). After slight displacement, the particle is set free. Find angular frequency of osciallation (in rad/sec) (Take g=10 m/ s^(2))
View SolutionA particle moves along a circular path a radius 15 cm with a constant angular acceleration of 4 "rad/s"^(2). If the initial angular speed of the particle was 5 rad/s. Find its angular displacement in 5 seconds.
View Solutionएक कण जिसका द्रव्यमान 20 g है बिंदु (2 m, 8 m) से, विरामावस्था से गिराया जाता है | यहाँ y-अक्ष ऊपर कि ओर ऊर्ध्वाधर दिशा में लिया गया है (चित्र 16.8) | एक सेकंड बाद मूलबिंदु के प्रति कण का कोणीय संवेग निकालें g=10m/s2 लें |

View SolutionAngular velocity of smooth parabolic wire y = 4c(x^2) about axis of parabola in vertical plane if bead of mass m does not slip at (a,b) will be
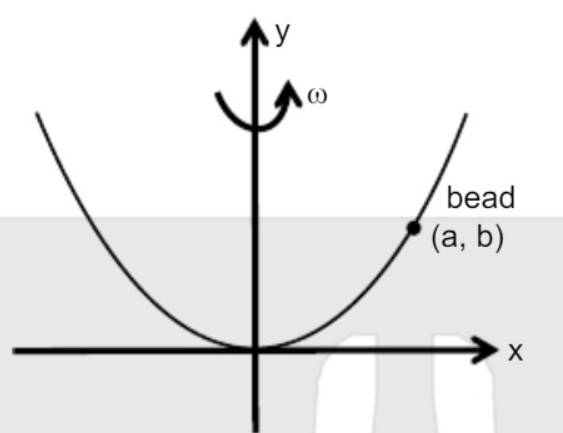
View SolutionAngular velocity of smooth parabolic wire y = 4c(x)^(2) about axis of parabola in vertical plane if bead of mass m does not slip at (a,b) will be

View SolutionA particle is placed at the lowest point of a smooth parabola having the equation x2=5y( x,y are in metre). After a slight displacement, the particle is constrained to move along the parabola. Find the angular frequency of oscillations (in rad/sec).
View Solutionएक कण X-Y तल में, (y-अक्ष उर्ध्वाधर) प्रक्षेपित किया जाता है। प्रक्षेपण के 2 sec बाद कण का वेग x अक्ष से 45∘ के कोण पर है, तथा प्रक्षेपण के 4 sec बाद यह क्षैतिज गति कर रहा है। प्रक्षेपण वेग ज्ञात करो।
View Solution

