A particle is projected from ground at some angle with the horizontal. Let P be the point at maximum height H. At what height above the point P should the particle be aimed to have range equal to maximum height ?
H
2 H
H//2
3 H
The correct Answer is:A
To solve the problem, we need to determine the height above point P (the maximum height H) to which the particle should be aimed so that the range equals the maximum height. Let's break it down step by step.
Step 1: Understand the Problem
We know that a particle is projected at an angle and reaches a maximum height H. We need to find a height h above point P such that when the particle is aimed at this height, the range R of the projectile equals H.
Step 2: Relate Range and Maximum Height
From the projectile motion equations, we know that the range R of a projectile is given by:
R=v2sin(2θ)g
And the maximum height H is given by:
H=v2sin2(θ)2g
Given that we want R=H, we can set these two equations equal to each other.
Step 3: Use the Relationship Between Range and Height
Since we know that R=H, we can express this as:
v2sin(2θ)g=v2sin2(θ)2g
This simplifies to:
sin(2θ)=12sin2(θ)
Step 4: Find the Angle
Using the identity sin(2θ)=2sin(θ)cos(θ), we can rewrite the equation:
2sin(θ)cos(θ)=12sin2(θ)
This can be rearranged to find tan(θ).
Step 5: Relate Height Above Point P
Let C be the point where the particle should be aimed. We can express the height h above point P as:
h=H+PC
Where PC is the vertical distance from point P to point C.
Step 6: Set Up the Equation
From the geometry of the projectile motion, we can relate the distances:
R=2H
This means that the height h above point P should equal the maximum height H.
Step 7: Conclusion
Thus, the height h above point P is equal to the maximum height H:
h=H
Final Answer
The height above point P should be equal to the maximum height H.
---
We know that a particle is projected at an angle and reaches a maximum height H. We need to find a height h above point P such that when the particle is aimed at this height, the range R of the projectile equals H.
From the projectile motion equations, we know that the range R of a projectile is given by:
R=v2sin(2θ)g
And the maximum height H is given by:
H=v2sin2(θ)2g
Given that we want R=H, we can set these two equations equal to each other.
Since we know that R=H, we can express this as:
v2sin(2θ)g=v2sin2(θ)2g
This simplifies to:
sin(2θ)=12sin2(θ)
Using the identity sin(2θ)=2sin(θ)cos(θ), we can rewrite the equation:
2sin(θ)cos(θ)=12sin2(θ)
This can be rearranged to find tan(θ).
Let C be the point where the particle should be aimed. We can express the height h above point P as:
h=H+PC
Where PC is the vertical distance from point P to point C.
From the geometry of the projectile motion, we can relate the distances:
R=2H
This means that the height h above point P should equal the maximum height H.
Thus, the height h above point P is equal to the maximum height H:
h=H
The height above point P should be equal to the maximum height H.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning
5 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Subjective
39 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A river is flowing towards with a velocity of 5ms−1. The boat velocity is 10ms−1. The boat crosses the river by shortest path. Hence,
View SolutionThe projectile has only vertical component of velocity at the highest point of its trajectory.
At the highest point, only one component of velocity is present.
View SolutionTwo particles were projected one by one with the same initial velocity from the same point on level ground. They follow the same parabolic trajectory and are found to be in the same horizontal level, separated by a distance of 1m,2s after the second partice was projected. Assume that the horizontal component of their velocities is 0.5ms−1. Find
(a) the horizontal range of the parabolic path.
(b) the maximum height for the parabolic path.
View SolutionA man in a lift ascending with an upward acceleration a throws a ball vertically upwards with a velocity v with respect to himself and catches it after t1 seconds. After wards when the lift is descending with the same acceleration a acting downwards the man again throws the ball vertically upwards with the same velocity with respect to him and catches it after t2 seconds?
View SolutionOne mole of an ideal monatomic gas undergoes a linear process from A to B , in which is pressure P and its volume V change as shown in figure .
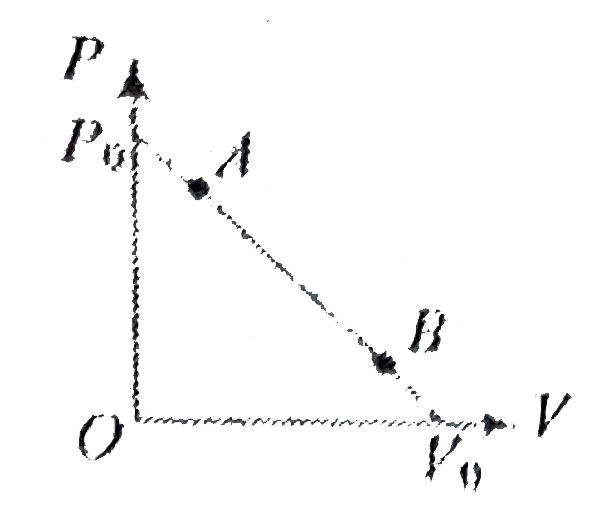
The absolute temperature T versus volume V for the given process is
View SolutionA particle is projected from ground at some angle with the horizontal. Let P be the point at maximum height H . At what height above the point P should the particlebe aimed to have equal to maximum height ?
View SolutionA particle is projected under gravity with velocity √2ag from a point at a height h above the level plane at an angle θ to it. The maximum range R on the grond is :
View SolutionA particle is thrown at an angle with horizontal from the ground. After 4s it reaches to a point P and after 5 more seconds it strikes the ground. Find the height of P the maximum height attained by the particle.
View SolutionAt what angle to the horizontal should an object be projected so that the maximum height reached is equal to the horizontal range.
View SolutionA particle is projected vertically upwards from a point O on the ground. It takes time t1 to reach a point A at a height h above the ground, it continues to move and takes a time t2 to reach the ground. Find (a) h, (b) the maximum height reached and (c ) the velocity of the partical at the half of maximum height.
View SolutionA body is projected obliquely from the ground such that its horizontal range is maximum.If the change in its maximum height to maximum height, is P , the change in its linear momentum as it travels from the point of projection to the landing point on the ground will be
View SolutionA particle is projected from ground with speed u and at an angle θ with horizontal. If at maximum height from ground, the speed of particle is 1/2 times of its initial velocity of projection, then find its maximum height attained.
View SolutionA body is projected obliquely from the ground such that its horizontal range is maximum. If the change in its linear momentum, as it moves from half the maximum height to maximum height, is P, the change in its linear momentum as it travels from the point of projection to the landing point on the ground will be:
View SolutionA particle is projected from ground at an angle theta with horizontal with speed u. The ratio of radius of curvature of its trajectory at point of projection to radius of curvature at maximum height is -
View SolutionA particle is projected from the top of a tower of height H. Initial velocity of projection is u at an angle theta above the horizontal . Particle hits the ground at a distance R from the bottom of tower. What should be the angle of projection theta so that R is maximum ? What is the maximum value of R?
View Solution

