A particle is projected with velocity 20√2m/s at 45∘ with horizontal. After 1s , find tangential and normal acceleration of the particle. Also, find radius of curvature of the trajectory at that point. (Take g=10m/s2)
The correct Answer is:A, B, D
To solve the problem step by step, we will use the following approach:
Step 1: Break down the initial velocity into components
The initial velocity u is given as 20√2m/s at an angle of 45∘ with the horizontal.
- The horizontal component ux is:
ux=ucos(45∘)=20√2⋅1√2=20m/s
- The vertical component uy is:
uy=usin(45∘)=20√2⋅1√2=20m/s
Step 2: Determine the velocity after 1 second
The horizontal velocity remains constant since there is no horizontal acceleration. The vertical velocity changes due to gravity.
- Horizontal velocity vx=ux=20m/s
- Vertical velocity after 1 second:
vy=uy−g⋅t=20−10⋅1=10m/s
Step 3: Calculate the total velocity after 1 second
The total velocity v can be calculated using the Pythagorean theorem:
v=√v2x+v2y=√(20)2+(10)2=√400+100=√500=10√5m/s
Step 4: Calculate the tangential acceleration
The tangential acceleration at is due to the change in the vertical component of the velocity. Since the only acceleration acting on the particle is gravity, the tangential acceleration is:
at=−g=−10m/s2
Step 5: Calculate the normal acceleration
The normal acceleration an can be calculated using the formula:
an=v2R
where R is the radius of curvature. We will first find the radius of curvature in the next step.
Step 6: Calculate the radius of curvature
The radius of curvature R can be calculated using the formula:
R=v2g=(10√5)210=50010=50m
Step 7: Calculate the normal acceleration using the radius of curvature
Now we can find the normal acceleration:
an=v2R=(10√5)250=50050=10m/s2
Final Results
- Tangential acceleration at=−10m/s2
- Normal acceleration an=10m/s2
- Radius of curvature R=50m
The initial velocity u is given as 20√2m/s at an angle of 45∘ with the horizontal.
ux=ucos(45∘)=20√2⋅1√2=20m/s
uy=usin(45∘)=20√2⋅1√2=20m/s
The horizontal velocity remains constant since there is no horizontal acceleration. The vertical velocity changes due to gravity.
vy=uy−g⋅t=20−10⋅1=10m/s
The total velocity v can be calculated using the Pythagorean theorem:
v=√v2x+v2y=√(20)2+(10)2=√400+100=√500=10√5m/s
The tangential acceleration at is due to the change in the vertical component of the velocity. Since the only acceleration acting on the particle is gravity, the tangential acceleration is:
at=−g=−10m/s2
The normal acceleration an can be calculated using the formula:
an=v2R
where R is the radius of curvature. We will first find the radius of curvature in the next step.
The radius of curvature R can be calculated using the formula:
R=v2g=(10√5)210=50010=50m
Now we can find the normal acceleration:
an=v2R=(10√5)250=50050=10m/s2
- Tangential acceleration at=−10m/s2
- Normal acceleration an=10m/s2
- Radius of curvature R=50m
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Subjective Questions
2 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - JEE Main
23 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Comprehension Based
5 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A particle is given an intial speed u inside a smooth spherical shell of radius R so that it is just able to complete the circle. Acceleration of the particle, when its velocity is vertical, is

View SolutionThe magnitude of displacement of a particle moving in a circle of radius a with constant angular speed ω varries with time t is
View SolutionA ball with mass m is attached to the end of a rod of mass M and length l. The other end of the rod is pivoted so that the ball can move in a vartical circle. The rod is held in the horizontal position as shown in figure and then given just enough a downward push so that the ball swings down and just reaches the vertical upward position having zero speed there. Now answer the following questions.
The change in potential energy of the system (ball+rod) is
View SolutionA ladder AP of length 5m inclined to a vertical wall is slipping over a horizontal surface with velocity of 2m/s, when A is at distance 3m from ground. What is the velocity of COM at this moment?

View SolutionMajor parts of communications systems are:
View SolutionA particle is projected with velocity 20sqrt(2)m//s at 45^(@) with horizontal. After 1s , find tangential and normal acceleration of the particle. Also, find radius of curveture of the trajectory at that point. (Take g=10m//s^(2))
View SolutionA particle of mass m=1kg is projected with speed u=20sqrt(2)m//s at angle theta=45^(@) with horizontal find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle is projected at angle theta with horizontal with velocity v_0 at t = 0 . Find (a) tangential and normal acceleration of the particle at t = 0 and at highest point of its trajectory. (b) the radius of curvature att = 0 and highest point. .
View SolutionA particle is projected with velocity 20√2m/s at 45∘ with horizontal. After 1s(g=10m/s2) match the following table
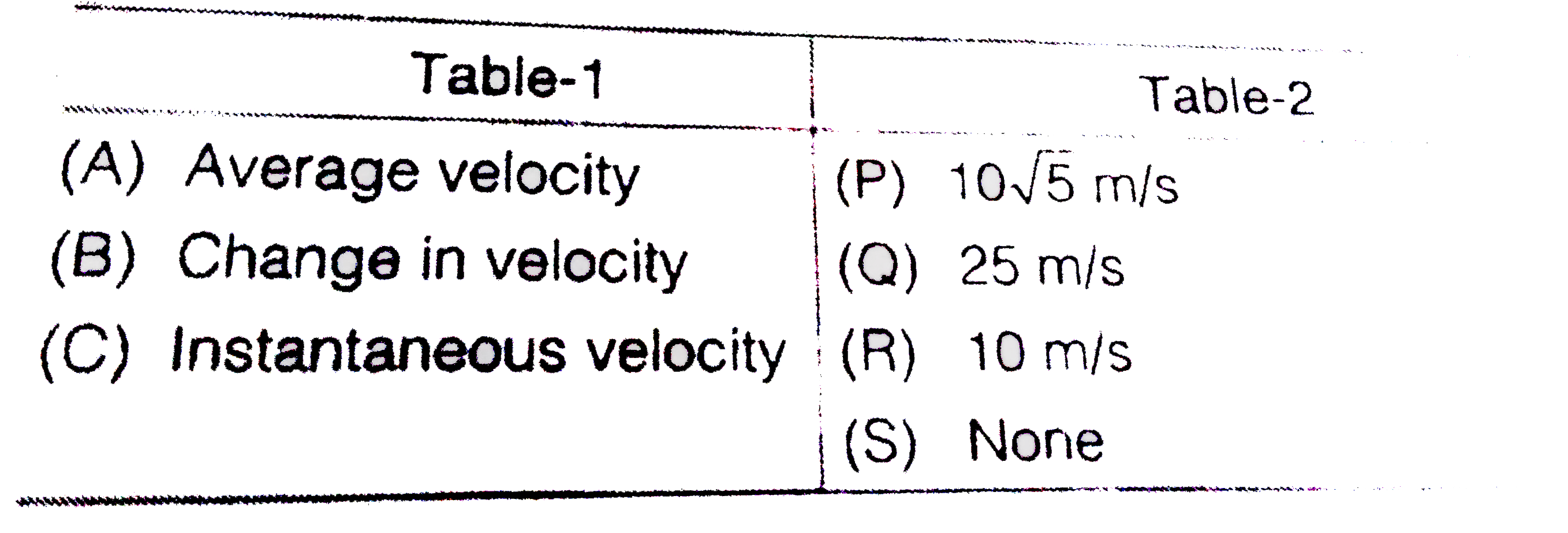
View SolutionA particle of mass 50 g is projected horizontally from the top of a tower of height 50 m with a velocity 20m/s. If g=10m/s2, then find the :-
View SolutionA particle of mass m=3kg is projected at an angle of 45^(@) with the horizontal with a speed of 20sqrt(2)m//s . The angular momentum of the particle at the highest point of trajectory about a horizontal axis passing through the origin and perpendicular to the plane of motion is
View SolutionA particle of 2m is projected at an angle of 45°with horizontal with a velocity of 20√2 m/s. After 1 sec. explosion takes place and the particle is broken into two equal pieces. As a result of expansion one point comes to rests. The maximum height from the ground attained by the other part is (g=10m/s2)
View SolutionA balll is projected with 20sqrt(2) m/s at angle 45^@ with horizontal, the angular velocity of the particle at highest point of its journey about point of projection is
View SolutionA particle of mass 2m is projected at an angle of 45∘ with the horizontal with a velocity of 20√2m/s, After 1s of explosion, the particle breaks into two equal pieces. As a result of this one part comes to rest. The maximum height from the ground attained by the other part is n×7m. Find n (g=10ms−2)
View SolutionA particle of mass m=1kg is projected with speed u=20√2m/s at angle θ=45∘ with horizontal find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View Solution

