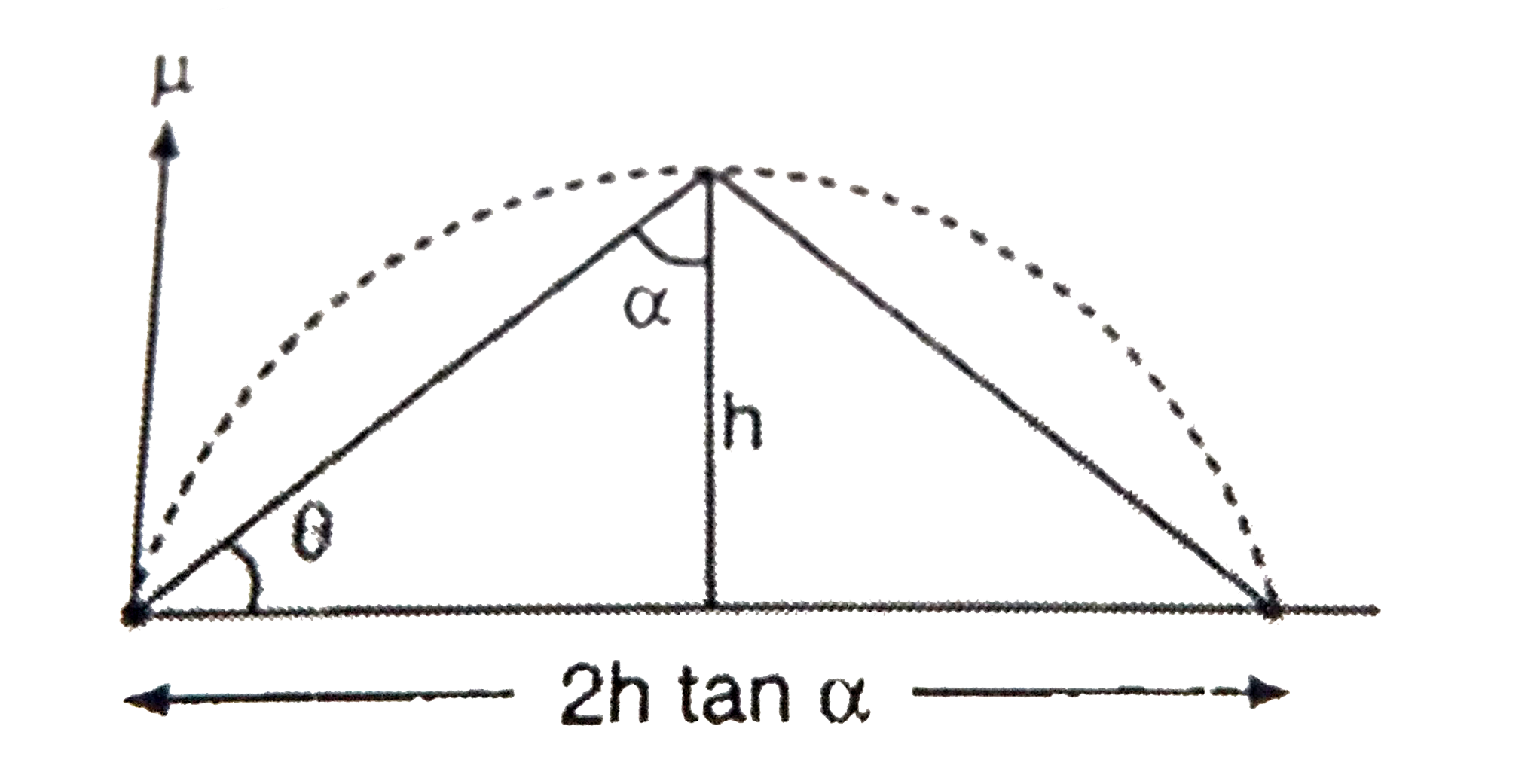
A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If αandβ be the base angles and θ the angle of projection, prove that tanθ=tanα+tanβ .
Let ABC be the triangle with base BC. Let h be the height of the vertex A above BC. If AM is the perpendicular drawn on base BC from vertex A, then tan∝=h/a and tanβ=H/B, where BM=aandCM=b.
Since A(a,h) lies on the trajectory of the projectile,
y=xtanθ(1−xR) ...(i)
Therefore, it should satisfy (i) i.e.,
h=atanθ(1−aa+b)[∵Ran≥,R=a+b]
ha=tanθ[ba+b]
⇒tanθ=ha+hb=tan∝+tanβ
Hence, proved.
 .
.
Topper's Solved these Questions
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Solved Examples
Explore 5 Videos
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise 5.1
Explore 15 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
Similar Questions
Two particle are projected with same initial velocities at an angle 30∘ and 60∘ with the horizontal .Then
View SolutionThe equation of projectile is y=16x−5x24. Find the horizontal range.
View SolutionA man in a lift ascending with an upward acceleration a throws a ball vertically upwards with a velocity v with respect to himself and catches it after t1 seconds. After wards when the lift is descending with the same acceleration a acting downwards the man again throws the ball vertically upwards with the same velocity with respect to him and catches it after t2 seconds?
View SolutionOne mole of an ideal monatomic gas undergoes a linear process from A to B , in which is pressure P and its volume V change as shown in figure .
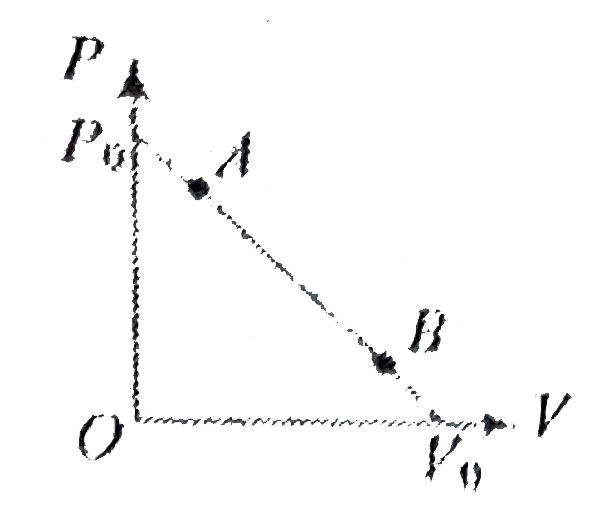
The absolute temperature T versus volume V for the given process is
View SolutionA particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If alpha and beta be the base angles and theta the angle of projection, prove that tan theta = tan alpha + tan beta .
View SolutionA particle is projected over a triangle from one extremity of its horizontal base. Grazing over the vertex, it falls on the other extremity of the base. If a and b are the base angles of the triangle and theta the angle of projection, prove that tan theta = tan prop + tan beta .
View SolutionA particle is projected over a traingle from one end of a horizontal base and grazing the vertex falls on the other end of the base. If alpha and beta be the base angles and theta the angle of projection, prove that tan theta = tan alpha + tan beta .
View SolutionA projectile is fired from the base of cone shaped hill. The projectle grazes the vertex and strikes the hill again at the base. If α be the half-angle of the cone, h its height, u the initial velocity of projection and θ angle of projection, then tanθtanα is:
View SolutionA particle is projected up an inclines plane. Plane is inclined at an angle theta with horizontal and particle is projected at an angle alpha with horizontal. If particle strikes the plane horizontally prove that tan alpha=2 tan theta
View SolutionA particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If alpha and beta are the base angles of triangle and angle of projection is theta , then prove that ( tan theta = tan alpha + tan beta)
View SolutionA particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If 30^(@) and 60^(@) be the base angles and theta the angle of projection then tan theta is
View SolutionA particle is projected over a triangle from one end of a horizontal base and garzing the vertex falls on the other end of the base . If α and β the base angles and θ the angle of projection then show that tanθ=tanα+tanβ.
View SolutionA particle is thrown over a triangle from one end of a horizontal base and grazing the vertex falls on the other end of the base. If alpha and beta be the base angles and theta be the angle of projection, prove that tan theta = tan alpha+ tan beta
View SolutionA particle is thrown over a triangle from one end of a horizontal base and grazing the vertex falls on the other end of the base. If α and β be the base angles and θ be the angle of projection, prove that tan θ=tanα+tanβ
View SolutionA particle is thrown over a triangle from one end of a horizontal base and grazing the vertex falls on the other end of the base. If α and β be the base angles and θ be the angle of projection, prove that tanθ=tanα+tanβ.
View SolutionA particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If αandβ be the base angles and θ the angle of projection, prove that tanθ=tanα+tanβ .
View Solution
