A particle of charge q and mass m is suspended from a point on the wall by a rigid massless rod oflength L=3/m as shown. Above the point of suspension another particle is clamped which has a charge -q at a distance L .from point of suspension. On slight displacement from the mean position, the suspended particle is observed to executes SHM. Find the time period of SHM. (For calculations consider Kq2=2mgL2and g=π2)[4s]
![A particle of charge q and mass m is suspended from a point on the wall by a rigid massless rod oflength L = 3//m as shown. Above the point of suspension another particle is clamped which has a charge -q at a distance L .from point of suspension. On slight displacement from the mean position, the suspended particle is observed to executes SHM. Find the time period of SHM. (For calculations consider Kq^(2) = 2mgL^(2) and g = pi^(2)) [4s]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/GAL_PHY_V03A_ECA_C01_E01_121_Q01.png)
Step by step video & image solution for A particle of charge q and mass m is suspended from a point on the wall by a rigid massless rod oflength L = 3//m as shown. Above the point of suspension another particle is clamped which has a charge -q at a distance L .from point of suspension. On slight displacement from the mean position, the suspended particle is observed to executes SHM. Find the time period of SHM. (For calculations consider Kq^(2) = 2mgL^(2) and g = pi^(2)) [4s] by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A particle of mass m is suspended from a fixed point O by a string length l.At t=0, it is displaced from its equilibrium position and released.If T is the tension in the string with time t, then the correct graph is
View SolutionA charged particle of mass m having charge q remains in equilibrium at height d above a fixed charge Q. Now the charged particle is slightly displaced along the line joining the charges, show that it will executes S.H.M. and find the time period of oscillation.
View Solution
Knowledge Check
A particle of mass m is suspended from point O and undergoes circular motion in horizontal plane as conical pendulum as shown in figure.
 AAngular momentum of particle about point of suspension does not remains constant.BAngular momentum of particle about centre of circle remains constant.CAverage force during half rotation is 2mgtanthethaπDAverage torque about axis OC during half rotation is zero
AAngular momentum of particle about point of suspension does not remains constant.BAngular momentum of particle about centre of circle remains constant.CAverage force during half rotation is 2mgtanthethaπDAverage torque about axis OC during half rotation is zeroA particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
Arg√L2−r2Br√g(L2−r2)14Cr√g(L2−r2)12DmgL(L2−r2)12A simple pendulum of mass m and charge +q is suspended vertically by a massless thread of length l. At the point of suspension, a point charge +q is also fixed. If the pendulum is displaced slightly from equilibrium position, its time period will be
AT=2π ⎷lg+kq2ml2BT=2πCT=2π√lgDwill be greater then 2π√lg
The equation of motion of a particle executing S.H.M. is a=−bx, where a is the acceleration of the particle, x is the displacement from the mean position and b is a constant. What is the time period of the particle ?
View SolutionA spherical bob of mass m and radius R is attached to a fixed point by means of a massless rigid rod whose length from the point of support up to the centre of bob is l. Find the period of small oscillation.
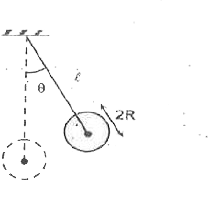
View SolutionA thin rod of length 1 m is suspended from its end and is made to oscillate in a vertical plane. The distance between the point of suspension and centre of oscillation will be :
View SolutionA particle of charge q is projected from point P with velocity v as shown. Choose the correct statement from the following.

View SolutionA positively charged particle of charge q and mass m is suspended from a point by a string of length l. In the space a uniform horizontal electric field E exists . The particle is drawn aside so that it is projected horizontally with velocity v such that the particle starts to move along a circle with same constant speed v. Find the speed v.

View Solution
