A particle of m=5kg is momentarily at rest at time t=0. It is acted upon by two forces →F1 and →F2. →F1= 70ˆj N. The direction and manitude of →F2 are unknown. The particle experiences a constant acceleration, →a,in the direction as shown in figure. Neglect gravity.
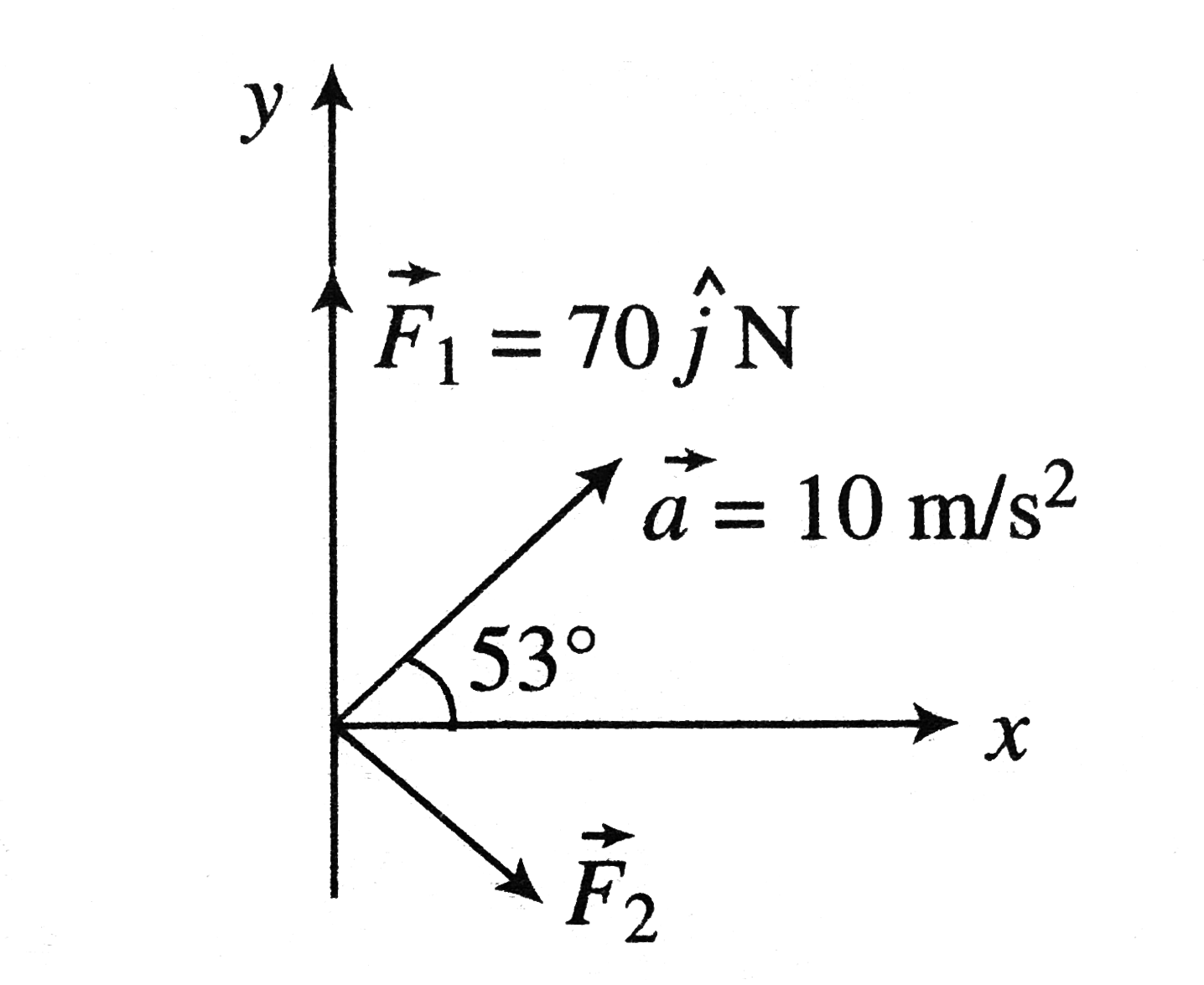
a.Find the missing force →F2.
b. What is the velocity vector of the particle at t=10s?
c. What third force, →F3 is required to make the acceleration of the particle zero? Either give magnitude and direction of →F3 or its components.
30ˆi+40ˆj
−(30ˆi+40ˆj)
40ˆi+30ˆj
−(40ˆi+30ˆj)
The correct Answer is:B
The sume of forces →F1+→F2=m→a
=5(10cosθˆi+10sinθˆj)=30ˆi+40ˆj
→F1+→F2+→F3=0
→F3=−(→F1+→F2)=−30ˆi−40ˆj
Similar Questions
A force F = (2 vec i + vec j + vec k)N is acting on a particle moving with constant velocity vec v = (vec i + 2 vec j + vec k)m/s . Power delivered by force is
View SolutionA particle moves with the velocity vec v = (5 vec i + 2 vec j - vec k) ms^(-1) under the influence of a constant force, vec F = (2 vec i + 5 vec j - 10 vec k)N . The instantaneous power applied is
View SolutionIf →F is the force acting in a particle having position vector →r and →τ be the torque of this force about the origin, then
View SolutionThe velocity of a particle varies with time as per the law vec(V) = vec(a) + vec(b)t where vec(a) and vec(b) are two constant vectors. The time at which velocity of the particle is perpendicular to velocity of the particle at t= 0 is
View SolutionA force vec F = 3 vec i + 2 vec j - 4 vec k is acting at the point (1,-1, 2) . Find the vector moment of vec F about the point (2,-1,3) .
View SolutionIf vec F is the force acting in a particle having position vector vec r and vec tau be the torque of this force about the origin, then
View SolutionThe momentum of a particle is vec P = 2 cos t hati + 2 sin t hat j . What is the angle between the force vec F acting on the particle and the momentum vec p ?
View SolutionIf →r and →F be the distance and force vectors. What meaning can be atteched to →r.→F and →rx→F ?
View Solution

