A particle of mass m is moving horizontally with a constant velocity v towards a rigid wall that is moving in opposite direction with a constant speed u. Assuming elastic impact between the particle and wall, the work done by the wall in reflecting the particle is equal to
(12)m(u+v)2
(12)m(u+v)
(12)muv
none of these
The correct Answer is:D
To solve the problem, we need to determine the work done by the wall in reflecting the particle after an elastic collision. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the initial conditions
The particle of mass m is moving towards a wall with a velocity v, while the wall is moving in the opposite direction with a velocity u.
Step 2: Determine the velocity of approach
Before the collision, the total velocity of approach is the sum of the velocities of the particle and the wall:
\(
\text{Velocity of approach} = v + u
\)
Step 3: Use the principle of elastic collision
In an elastic collision, the coefficient of restitution (e) is equal to 1. This means that the velocity of separation after the collision will equal the velocity of approach before the collision.
Step 4: Write the equation for velocity of separation
Let \( v' \) be the velocity of the particle after the collision. The velocity of separation can be expressed as:
\(
\text{Velocity of separation} = v' - (-u) = v' + u
\)
According to the principle of restitution:
\(
v' + u = v + u
\)
This simplifies to:
\(
v' = 2u + v
\)
Step 5: Calculate the change in kinetic energy
The work done by the wall on the particle is equal to the change in kinetic energy of the particle. The initial kinetic energy (KE_initial) and final kinetic energy (KE_final) can be expressed as:
\(
\text{KE_initial} = \frac{1}{2} m v^2
\)
\(
\text{KE_final} = \frac{1}{2} m (v')^2 = \frac{1}{2} m (2u + v)^2
\)
Step 6: Calculate the work done
The work done (W) by the wall is the change in kinetic energy:
\(
W = \text{KE_final} - \text{KE_initial}
\)
Substituting the expressions for kinetic energy:
\(
W = \frac{1}{2} m (2u + v)^2 - \frac{1}{2} m v^2
\)
Step 7: Simplify the expression
Using the formula \( a^2 - b^2 = (a - b)(a + b) \):
\(
W = \frac{1}{2} m \left( (2u + v)^2 - v^2 \right)
\)
\(
= \frac{1}{2} m \left( (4u^2 + 4uv + v^2) - v^2 \right)
\)
\(
= \frac{1}{2} m (4u^2 + 4uv)
\)
\(
= 2m(2u^2 + 2uv)
\)
Thus, the work done by the wall in reflecting the particle is:
\(
W = 2m(u^2 + uv)
\)
Final Answer
The work done by the wall in reflecting the particle is:
\(
W = 2m(u^2 + uv)
\)
The particle of mass m is moving towards a wall with a velocity v, while the wall is moving in the opposite direction with a velocity u.
Before the collision, the total velocity of approach is the sum of the velocities of the particle and the wall:
\(
\text{Velocity of approach} = v + u
\)
In an elastic collision, the coefficient of restitution (e) is equal to 1. This means that the velocity of separation after the collision will equal the velocity of approach before the collision.
Let \( v' \) be the velocity of the particle after the collision. The velocity of separation can be expressed as:
\(
\text{Velocity of separation} = v' - (-u) = v' + u
\)
According to the principle of restitution:
\(
v' + u = v + u
\)
This simplifies to:
\(
v' = 2u + v
\)
The work done by the wall on the particle is equal to the change in kinetic energy of the particle. The initial kinetic energy (KE_initial) and final kinetic energy (KE_final) can be expressed as:
\(
\text{KE_initial} = \frac{1}{2} m v^2
\)
\(
\text{KE_final} = \frac{1}{2} m (v')^2 = \frac{1}{2} m (2u + v)^2
\)
The work done (W) by the wall is the change in kinetic energy:
\(
W = \text{KE_final} - \text{KE_initial}
\)
Substituting the expressions for kinetic energy:
\(
W = \frac{1}{2} m (2u + v)^2 - \frac{1}{2} m v^2
\)
Using the formula \( a^2 - b^2 = (a - b)(a + b) \):
\(
W = \frac{1}{2} m \left( (2u + v)^2 - v^2 \right)
\)
\(
= \frac{1}{2} m \left( (4u^2 + 4uv + v^2) - v^2 \right)
\)
\(
= \frac{1}{2} m (4u^2 + 4uv)
\)
\(
= 2m(2u^2 + 2uv)
\)
\(
W = 2m(u^2 + uv)
\)
The work done by the wall in reflecting the particle is:
\(
W = 2m(u^2 + uv)
\)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A ball strikes a smooth horizontal floor obliquely and rebounds inelastically.
View SolutionStatement I: In a two-body collision, the momenta of the particles are equal and opposite to one another, before as well as after the collision when measured in the centre of mass frame.
Statement. II: The momentum of the system is zero from the centre of mass frame.
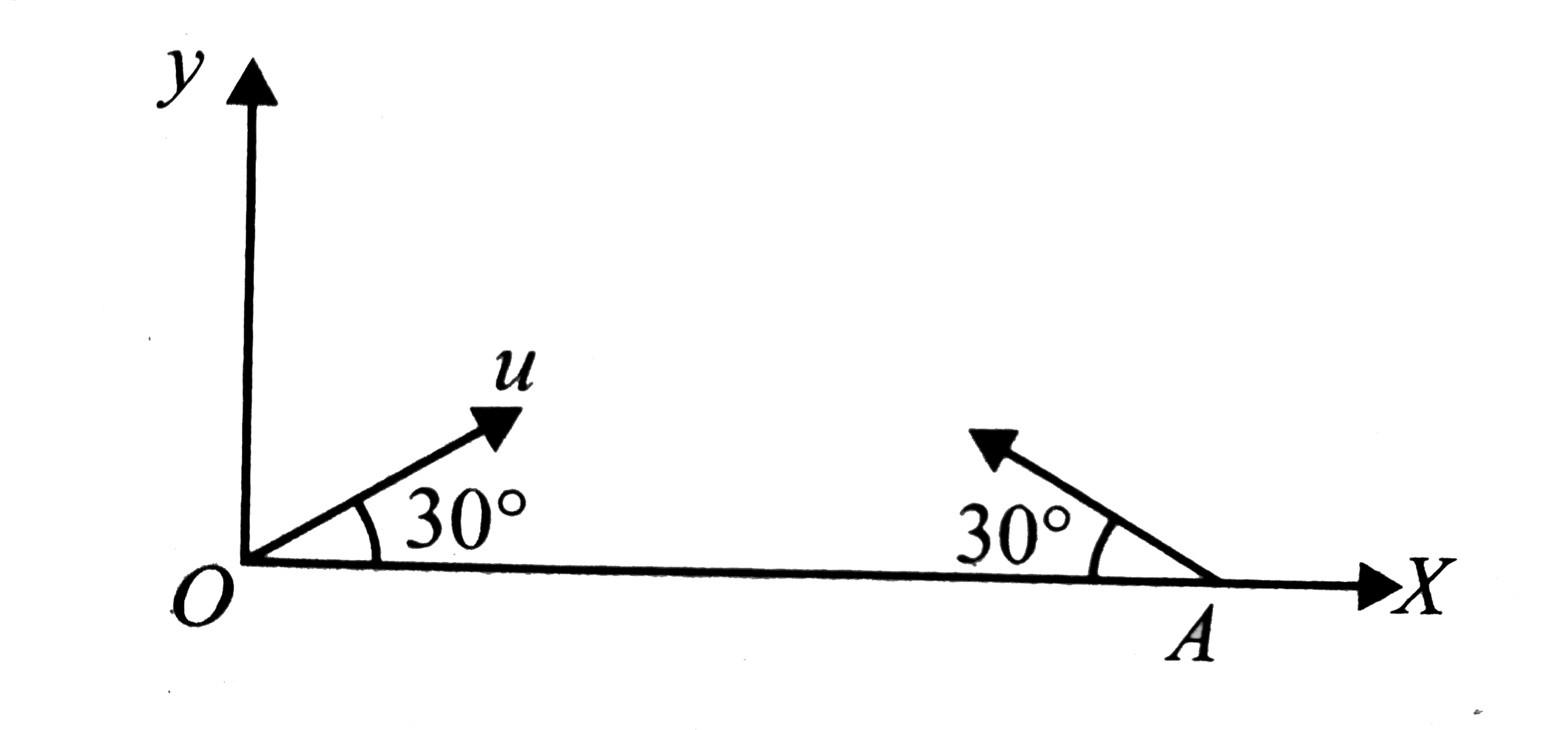
View SolutionTwo identical smooth balls are projected from points O and A on the horizontal ground with same speed of projection. The angle of projection in each case is 30∘.The distance between O and A is 100m. The balls collide in mid-air and return to their respective points of projection. If the coefficient of restitution is 0.7, find the speed of projection of either ball (in m/s) correct to nearest integer. (Take g=10ms−2 and √3=1.7)
View SolutionA colorimeter contains 400g of water at a temperature of 5∘C. Then, 200g of water at a temperature of +10∘C and 400g of ice at a temperature of −60∘C are added. What is the final temperature of the contents of calorimeter?
Specific heat capacity of water −1000 cal/kg/K
Specific latent heat of fusion of ice =80×1000 cal/kg
Relative specific heat of ice =0.5
View SolutionTo find the distance d over which a signal can be seen clearly in foggy conditions, a railways-engineer uses dimensions and assumes that the distance depends on the mass density ρ of the fog, intensity (power/area) S of the light from the signal and its frequency f. the engineer finds that d is proportional to S1/n. the value of n is
View SolutionA particle of mass m is moving horizontally with a constant velocity v towards a rigid wall that is moving in opposite direction with a constant speed u . Assuming elastic impact between the particle and wall, the work done by the wall in reflecting the particle is equal to
View SolutionA ball moving with a velocity v hits a massive wall moving towards the ball with a velocity a. An elastic impact lasts for time /_\t
View Solution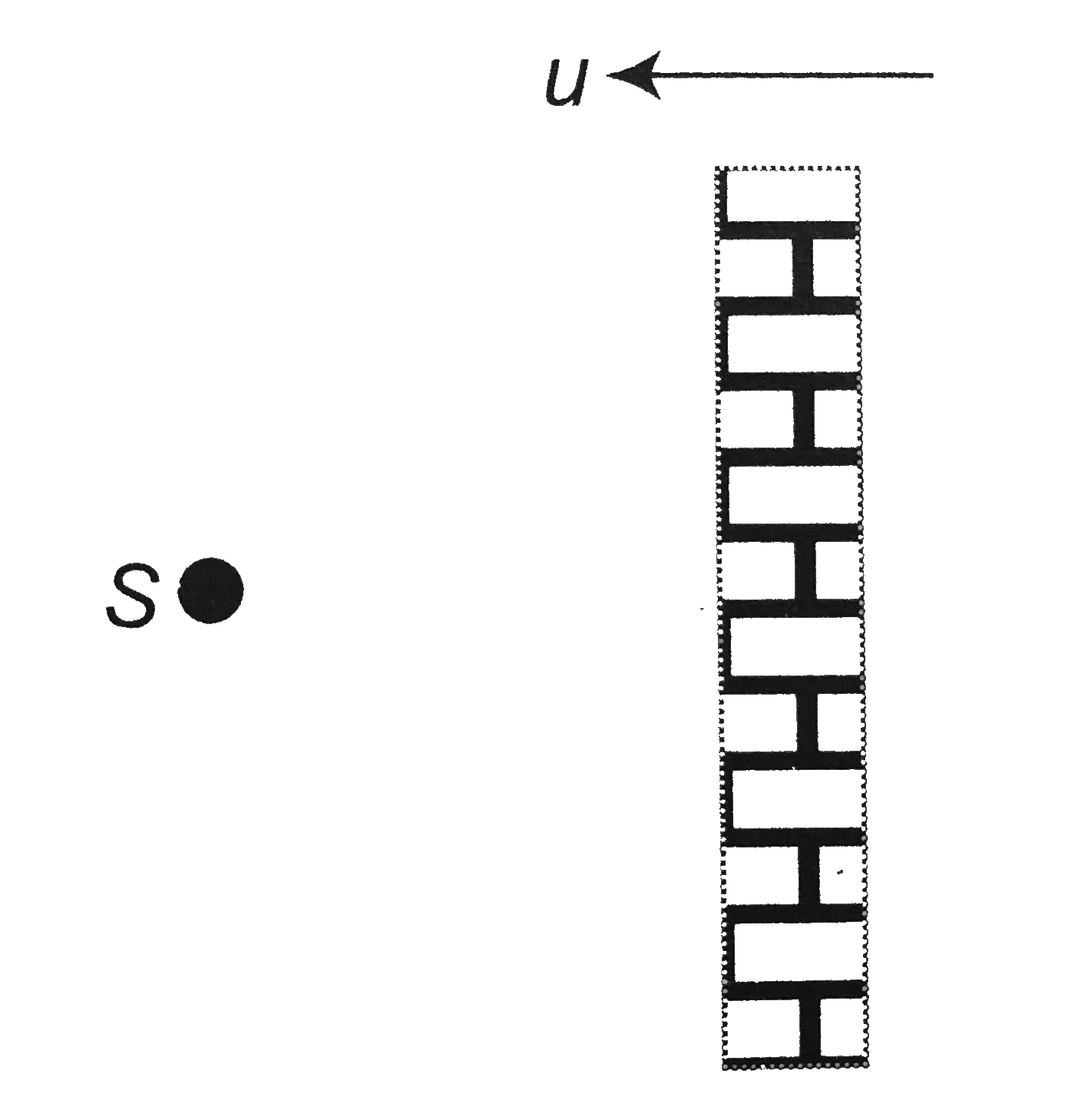
A wall is moving with constant velocity u towards a fixed source of sound of frequency f. The velocity of sound is v. The wavelength of the sound reflected by the wall is
View SolutionOn a particle moving on a circular path with constant speed v , light is thrown from a projectors placed at the centre of the circular path. The shadow of the particle is formed on the wall. The velocity of shadow up the wall is
View SolutionA stream of particles each of mass m moving with velocity v with number of particles per unit volume n strike against a wall at an angle theta to the normal elastically. Find the pressure exerted by the exerted by the stream on the wall.
View SolutionA ball moving with a velocity v strikes a wall moving toward the wall with a velocity u. An elastic impact occurs. Determine the velocity of the ball after the impact. What is the cause of the change in the kinetic energy of the ball ? Consider the mass of the wall to be infinitely great.
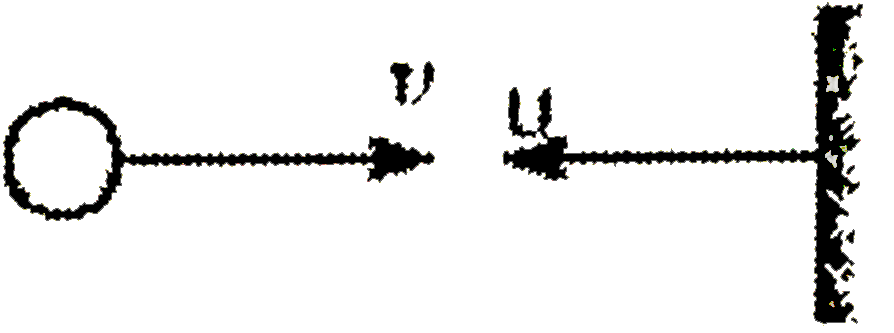
View SolutionA sphere moving with velocityv strikes elastically with a wall moving towards the sphere with a velocity u. If the mass of the wall is infinitely large, the work done by the wall during collision wiHbe:
View SolutionA Sphere moving with velocity v strikes a wall moving towards the sphere with a velocity u. If the mass of the wall is infinitely large the work done by the wall during collision will be:
View SolutionA particle of mass m strikes elastically on a wall with velocity v, at an angle of 60∘ from the wall then magnitude of change in momentum of ball along the wall is
View SolutionA particle of mass m strikes a wall with speed v at an angle 30^(@) with the wall elastically as shown in the figure. The magnitude of impulse imparted to the ball by the wall is
View Solution

