A particle starts travelling on a circle with constant tangential acceleration. The angle between velocity vector and acceleration vector, at the moment when particle completes half the circular track. Is
A
tan−1(2π)
B
tan−1(π)
C
tan−1(3π)
D
zero
Video Solution
Text Solution
The correct Answer is:A
v=√2ats=√2at(πR)

∴ an=v2R=2πat
or anat=2π⇒tanθ=anat=2π
∴ θ=tan−1(2π)
|
Similar Questions
Knowledge Check
A particle is moving in a circle with a constant speed, the acceleration of the particle has
Aconstant magnitudeBconstant magnitude and directionCboth magnitude and direction changesDneither magnitude nor direction changesIn uniform circular motion, the velocity vector and acceleration vector are
APerpendicular to each otherBSame directionCOpposite directionDNot related to each otherVelocity vector and acceleration vector in a uniform circular motion are related as
Aboth in the same directionBperpendicular to each otherCboth in oppsite directionDnot related to each other
A particle is moving in a circular orbit when a constant tangential acceleration. After 2s from the beginning of motion, angle between the total acceleration vector and the radius E becomes 45∘. What is the angular acceleration of the particle?
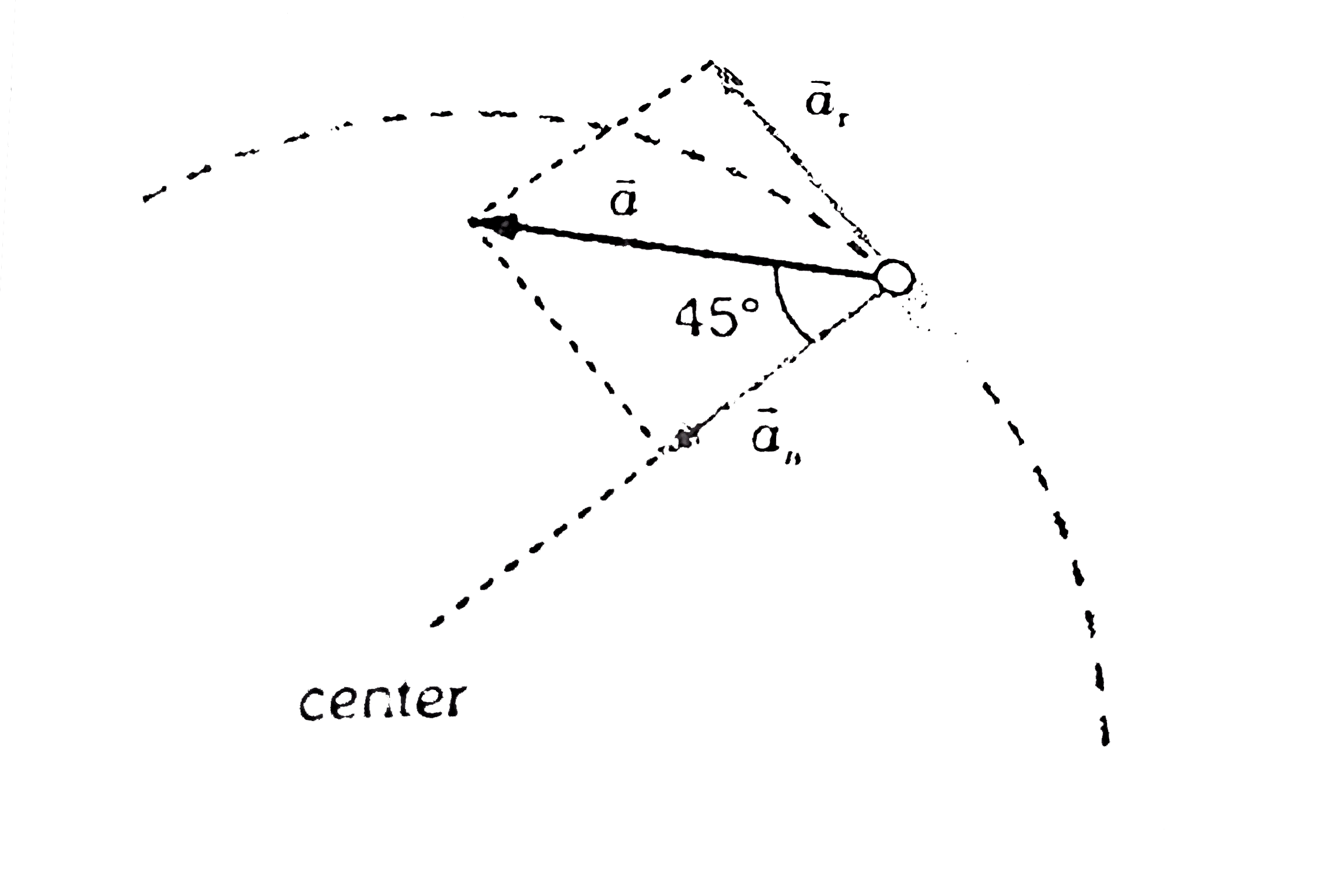
View SolutionVelocity vector and acceleration vector in a uniform circular motion are related as
View SolutionAngle between radius vector and centripetal acceleration is
View SolutionA particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
View SolutionA particle revolves round a circular path with a constant speed the acceleration of the particle is :
View Solution

