A positively charged particle of charge 1C and mass 40g, is revolving along a circle, of radius 40cm with velocity 5ms in a uniform magnetic field with centre at origin 0 in xy-plane. At t=0, the particle was at (0,0.4m,0) and velocity was directed along positive x-direction. Another particle having charge 1C and mass 10g moving uniformly parallel to z-direction 40 with velocity 40πmscollides with revolving particle at t=0 andgets stuck with it. Neglecting 7C gravitational force and colombians force, calculate x,y and z-coordinates of the combined particle at t=π40sec
In three dimensional co-ordinate system, axes are assumed according to right hand screw rule.
Consider such a system shown in Fig. In this system positive z direction is normal to plane of paper and is directed towards the reader.
The particle is positively charged, centre of its circular path is at origin and when the particle is on positive y-axis , its velocity is directed along positive x-direction, it means that the particle is moving clockwise

Since the particle is positively charged, therefore, current associated with its motion is also clockwise or along positive x direction at (0,0.4,0).
Lorentz's force is toward origin. Therefore, according to Fleming's left hand rule, magnetic induction B must be along positive z-direction.
Radius of circular path followed by this particle is r1=0.4m
But r1=m1v1q1B⇒B=m1v1q1r10.5T
Now the second particle collides and gets struck with it. Velocity of combined particle can be found out by applying law of conservation of momentum.
(m1+m2)→v=m1→v1+m2→v2
(40×10−3+10×10−3)→v
=(40×10−3)×5ˆi+(10×10−3)40πˆk
∴ x-direction of velocity of combined particle is vx=4ms−1
and z-direction, vz=8πms−1
Due to vx, combined particle tries to move clockwise along a circular path and due to vzit ties to move uniformly along z-axis.
Therefore, its ultimate path becomes helix. Radius of this helix is
R=(m1+m2)vx(q1+q2)B=0.2m
and period of revolution T=2π(m1+m2)(q1+q2)B=π10s
The particle turns by angle π/2 in time π/4s.
∴ x-coordinate of new position of combined particle =R=0.2m
→ y-coordinate=r1−R=0.2m
and z-direction =vzt=0.2m
 .
.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.1
22 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.2
13 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
A charged particle of mass 5 mg and charge q=+2μC has velocity →v=2ˆi−3ˆj+4ˆk. Find out the magnetic force on the charged particle and its acceleration at this instant due to magnetic field →B=3ˆj−2ˆk.→vand→B are in ms−1andWbm−2 , respectively.
View SolutionA wire is bent in the form of an equilateral triangle PQR of side 10 cm and carries a current of 5.0 A. It is placed in a magnetic field B of magnitude 2.0 T directed perpendicularly to the plane of the loop. Find the forces on the three sides of the triangle.
View SolutionWhich of the following statements is correct in the given figure?
Infinitely long wire at E kept perpendicular to paper carrying current inwards:

View SolutionLight is incident on a glass plate of refractive index 3.0 such that angle of refraction is 60° .Dark band is observed corresponding to the wavelength of 12000 A .If the thickness of glass plate is 1.2x10−3 mm. Calculate the order of the interference band for reflected system.
View SolutionIn an electrolytic solution the electric current is mainly due to the movement of free electrons.
View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0. Find the velocity vector and position vector of the particle vec v (t) and vec r (t) in relation with time.
View SolutionA positively charged particle having charge q_1 = 1 C and mass m_1 =40 gm is revolving along a circle of radius R=40 cm with velocity v_1 = 5 ms^-1 in a uniform magnetic field with center of circle at origin O of a three-dimensional system. At t=0 , the particle was at (0, 0.4m, 0) and velocity was directed along positive x direction. Another particle having charge q_2 = 1 C and mass m_2 = 10g moving uniformly parallel to positive z-direction with velocity v_2 = 40//pi ms^-1 collides with revolving particle at t=0 and gets stuck to it. Neglecting gravitational force and coulomb force, calculate x-, y- and z-coordinates of the combined particle at t= pi//40 s .
View SolutionThere exist uniform magnetic and electric fields of magnitudes 1T and 1Vm−1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms−1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time πs will be
View SolutionA charged particle (charge q, mass m) has velocity v_(0) at origin in +x direction. In space there is a uniform magnetic field B in -z direction. Find the y coordinate of particle when is crosses y axis.
View SolutionA positively charge particle moving along x -axis with a certain velocity enters a uniform electric field directed along positively y-axis. Its
View SolutionA particle having a charge of 10.0 mu C and mass 1 mug moves in a circle of radius 10 cm under the influence of a magnetic field of induction0.1 T. When the particle is at a point P, a uniform electric field is switched on so that the particle starts moving along the tangent with a uniform velocity. The electric field is
View SolutionPositively charged particles are projected into a magnetic field. If the direction of the magnetic field is along the direction of motion of the charged particles, the particles get
View Solutionएक समान चुंबकीय क्षेत्र की दिशा के अनुदिश एक आवेशित कण प्रक्षेपित किया जाता है। तब इसका वेग
View SolutionA positively charged particle moving along x-axis with a certain velocity enters a uniform electric field directed along positive y-axis. Its
View Solution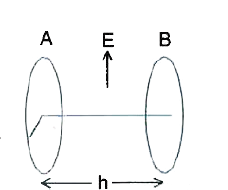
Two circular rings A and B each of radius 30 cm are placed coaxially with their axes horizontal in a uniform electric field E=105NC−1 directed vertically up. Distance between the centres of these rings is h = 40 cm. Ring A has a positive charge q1=10μC, while ring B has a negative charge of magnitude 20μC. A particle of mass m= 100 g and carrying a positive charge 104μC is released from rest at t=0 at the centre of the ring A. Find the velocity of the particle when it has moved through 40 cm? (g=10ms−2)
View SolutionA positively charged particle moving along x - axis with a certain velocity enters a uniform electric field directed along positive y-axis. Its
View Solution

