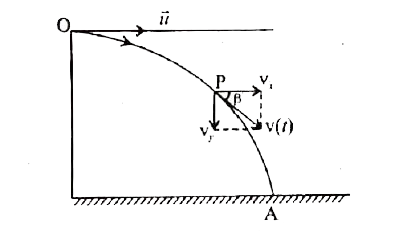
A projectile is fired horizontally with a velocity u. obtain the expression for resultant velocity of the projectile at any instant .Solution in Tamil
At any instant t, at the velocity components of the projectile along both x-axis and y-axis. The resultant of these two components gives the velocity of the projectile at that instant t, as shown in the figure .
The velocity component at any instant of the t along horizontal (x-axis) is vx=ux+axt
Since , ux=u,ax=0 , we get
vx=u
the component of velocity along vertical direction (y-axis) is given by vy=uy+ayt
vy=gt
∴ The velocity of the particle at any instant is
→v=uˆi+gtˆj
The speed of the particle at any instant t is given by
∴v=√v2x+v2y
v=√u2+g2t2
Similar Questions
A projectile is projected with speed u at an angle theta with the horizontal . The average velocity of the projectile between the instants it crosses the same level is
View SolutionA projectile is fired at an angle θ with horizontal. (a) Show that its trajectory is a parabola (b) Prove that for a given velocity of projection the horizontal range is same for (90∘−θ) (c) Obtain an expression for velocity of projectile at any instant.
View SolutionA projectile fired with velocity u at right angle to the slope which is inclined at an angle θ with horizontal. The expression for R is
View SolutionA projectile fired with velocity u at right angle to theslope which is inclined at an angle θ with horizontal. The expression for R is
View SolutionFor a projectile first with velocity u at an angle θ with the horizontal.

View SolutionA projectile is fired at an angle θ with the horizontal with velocity u. Deduce the expression for the maximum height reached by it.
View SolutionA projectile fired with velocity u at right angle to the slope which is inclined at an angle theta with horizontal. The expression for R is
View SolutionA projectile fired with velocity u at right angle to the slope which is inclined at an angle θ with horizontal. The expression for R is
View Solution

