A ring A which can slide on a smooth wire is connected to one end of a string as shown in fig. Other end of the string is connected to a hanging mass B. Find the speed of the ring when the string makes an angle θ with the wire and mass B is going down with a velocity v.
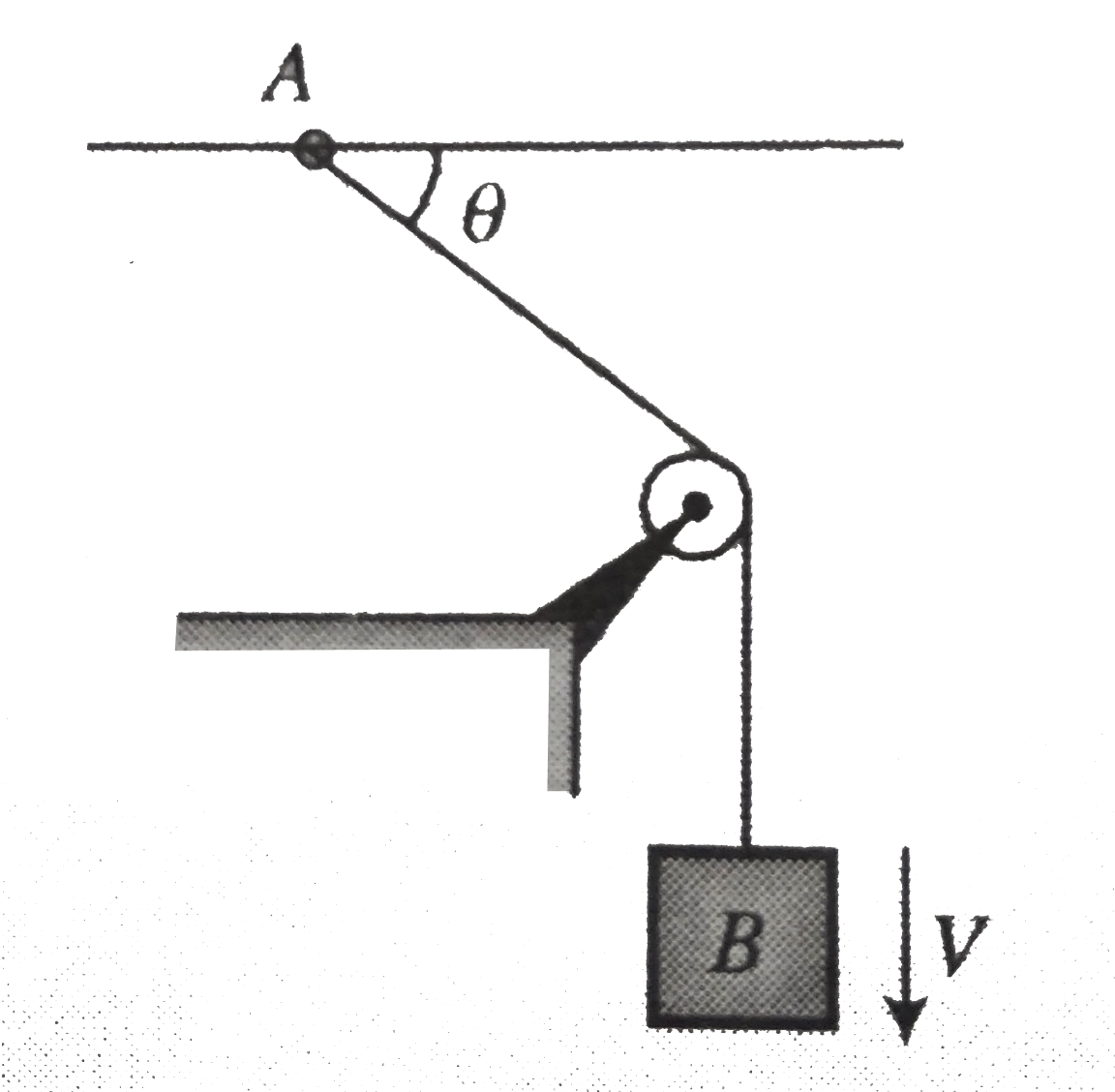
Let the speed of the ring is u, then ucosθ=v.Because components of velocity along the string should be same.
⇒u=v/cosθ=vsecθ.

Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.4
13 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective
15 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.2
35 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Video
Similar Questions
(a) A 10-kg block is supported by cord that runs to a spring scale, which is supported by another cord from the ceiling as shown in fig. What is the reading on the scale?

(b) In Fig. the block is supported by a cord that runs around a pulley and to a scale. The opposite end of the scale is attached by a cord to a wall. What is the reading of the scale?

(c ) In fig. the wall has been replaced with a second 10-kg block, what is the reading on the scale now?
 .
.
View SolutionA hot- air balloon consists of a basket, one passenger, and some carge. Let the total mass be M. Even though there is an upward lift force on the balloon, the balloon is initially acceleration downwards at a rate of g/3.
(a) Draw a free-body diagram for the descending balloon.
(b) Find the upward lift force in terms of the initial total weight Mg.
(c ) The passenger notices that he is heading straight for a waterfall and decides he needs to go up. What fraction of the total weight must he drop overboard so that the balloon accelerates upward at a rate of g/2? Assume that the upward lift force remains the same.
View SolutionAs per the diagram given in fig.

The free-body diagram of M is fig. (correct or incorrect). Assume all surface are frictionless.

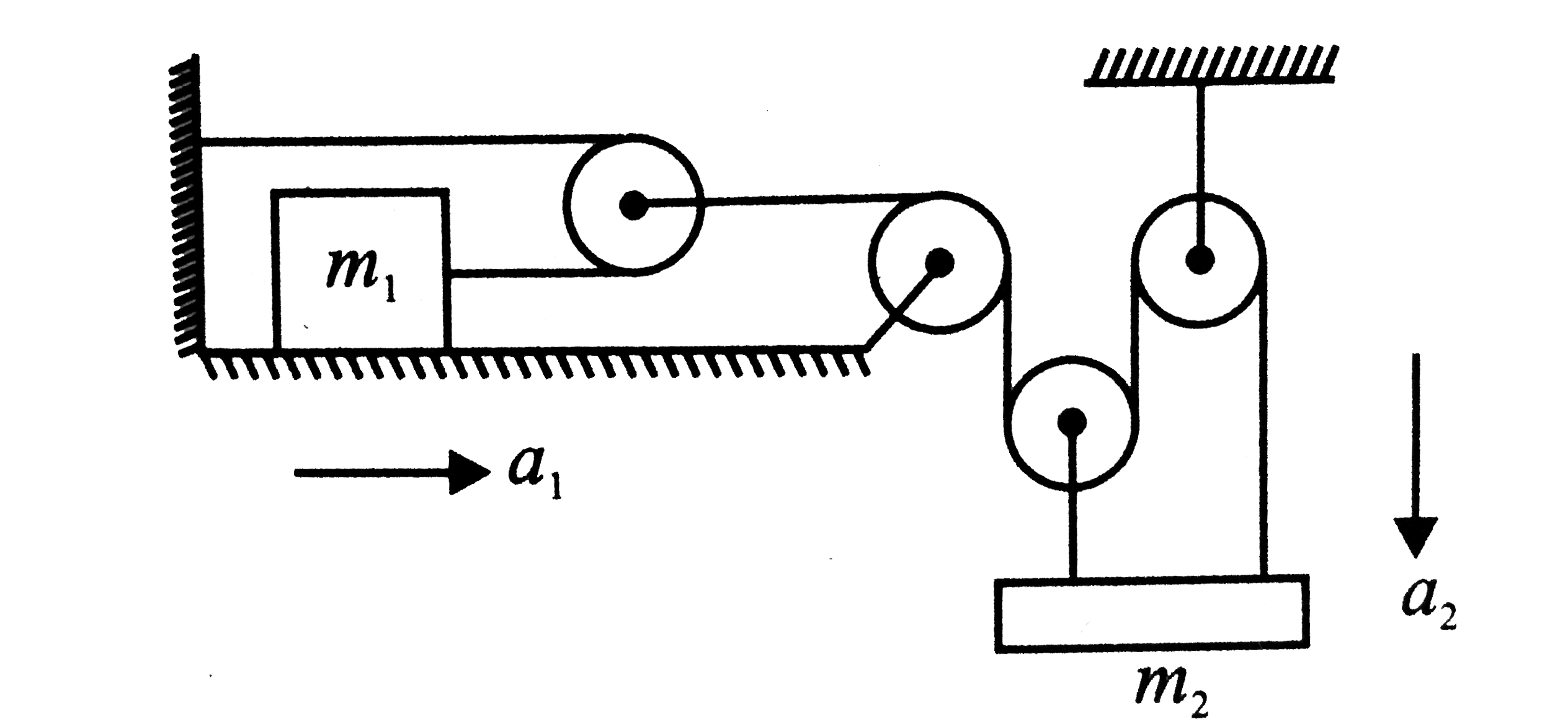
View SolutionTwo blocks are arranged as shown in figure. Find the ratio of a1/a2. (a1 is acceleration of m1 and a2 that of m2)
View SolutionA block is moving on an inclined plane making an angle 45∘ with the horizontal and the coefficient of friction is μ. The force required to just push it up the inclined plane is 3 times the force required to just prevent it from sliding down. If we define N=10μ, then N is
View SolutionTwo block A and B of mass M & 3M are connected through a light string. One end of the string is connected to the blcok B and its other end is connected to a fixed point S as shown in fig. Now a force F is applied to block B. find the acceleration of block A & B.
View SolutionA ring A which can slide on a smooth wire is connected to one end of a string as shown in fig. Other end of the string is connected to a hanging mass B. Find the speed of the ring when the string makes an angle theta with the wire and mass B is going down with a velocity v.
View SolutionA ring of mass m=1kg can slide over a smooth vertical rod. A light string attached to the ring passing over a smooth fixed pulley at a distance of L=0.7m from the rod as shown in figure. At the other end of the string mass M=5kg is attached, lying over a smooth fixed inclined plane of inclination angle 37^@ . The ring is held in level with the pulley and released. Determine the velocity of ring when the string makes an angle (alpha=37^@) with the horizontal. [sin 37^@=0.6]
View SolutionOne end of a 2.4 - m string is held fixed and the other end is attached to a weightless ring that can slide along a frictionless rod as shown in Fig. 7.86. The three longest possible wavelength for standing waves in this string are respectively
View SolutionA bead of mass m is threaded on a smooth circular wire centre O, radius a, which is fixed in vertical plane. A light string of natural olength 'a', elastic constant =3mga and breaking strength 3mg connects the bead to the lowest point A of the wire. The other end of the string is fixed to ring at point B near point A. The string is slaked initially. The bead is projected from A with speed u.
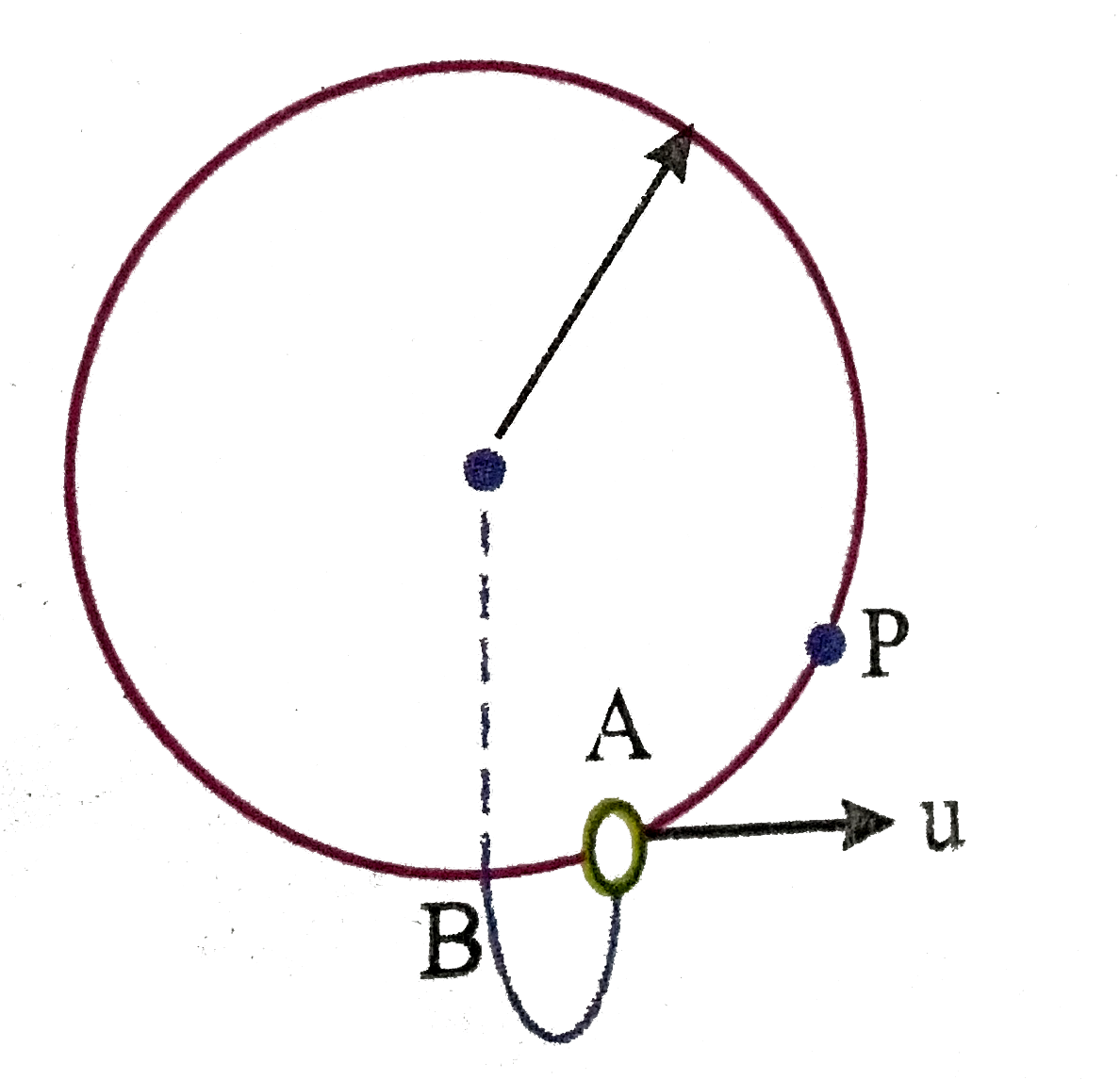
If v=2u0, the tension T in th elastic string when the bead is at the highest point B of the wire is
View SolutionA ring of mass m can slide on the vertical smooth rod. Ring is connected by block with string as shown in figure. Pulley is of mass-less and smooth the system is released from reast. Initial tension in string is
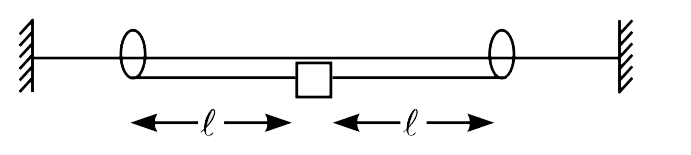
View SolutionTwo small rings each of mass ‘m’ are connected to a block of same mass ‘m’ through inextensible light strings. Rings are constrained to move along a smooth horizontal rod. Initially system is held at rest (as shown in figure) with the strings just taut. Length of each string is ‘l’. The system is released from the position shown. Find the speed of the block (v) and speed of the rings (u) when the strings make an angle of theta=60^(@)withvertical.(Takeg = 10 m//s^2)
View SolutionA smooth ring of mass m can slide on a fixed horizontal rod. A string tied to the ring pases over a fixed pulley B and carries a block C of mass 2m as shown below. As the ring starts sliding
View SolutionA small ring of mass m1 is connected by a string of length l to a small heavy bob of mass m2. The ring os free to move (slide) along a fixed smooth horizontal wire. The bob is given a small displacement from its equilibrium position at right angles to string. Find period of small oscillations.
_E01_106_Q01.png)
View SolutionA small ring of mass m is constrained to slide along a horizontal wire fixed between two rigid supports. The ring is connected to a particle of same mass by an ideal string & the whole system is released from rest as shown in the figure. If the coefficient of friction between ring A and wire is 35, the ring will start sliding when the connecting string will make an angle θ with the vertical, then θ will be (particle is free to move and ring can slide only)
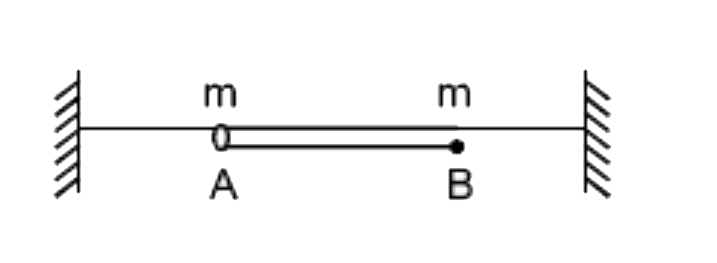
View Solution

