A rocket in launched vertically from the sruface of earth with an initial velocity u. Find the height up to which the rocket can go from the surface velocity u. Find t eh height up to which the rocket can go from the surface of earth before back or earth
To solve the problem of finding the maximum height a rocket can reach when launched vertically from the surface of the Earth with an initial velocity u, we can use the principle of conservation of energy. Here’s a step-by-step solution:
Step 1: Understand the Initial Energy
The initial energy of the rocket consists of its kinetic energy and gravitational potential energy at the surface of the Earth.
- Kinetic Energy (KE):
KE=12mu2
- Potential Energy (PE):
PE=−GMmR
where G is the universal gravitational constant, M is the mass of the Earth, m is the mass of the rocket, and R is the radius of the Earth.
Step 2: Total Initial Energy
The total initial energy Ei at the surface of the Earth is:
Ei=KE+PE=12mu2−GMmR
Step 3: Final Energy at Maximum Height
At the maximum height h, the rocket will momentarily stop, so its kinetic energy will be zero. The potential energy at height h can be expressed as:
PE=−GMmR+h
Step 4: Apply Conservation of Energy
According to the conservation of energy, the initial energy must equal the final energy:
Ei=Ef
Substituting the expressions for initial and final energy:
12mu2−GMmR=−GMmR+h
Step 5: Simplify the Equation
We can cancel m from the equation (assuming m≠0):
12u2−GMR=−GMR+h
Rearranging gives:
12u2=GMR−GMR+h
Step 6: Combine the Terms
Finding a common denominator for the right side:
12u2=GM(R+h−R)R(R+h)=GMhR(R+h)
Step 7: Solve for Height h
Now, we can solve for h:
h=u2R(R+h)2GM
This can be rearranged to isolate h:
h=u2R2GM−u2
Final Result
Thus, the maximum height h that the rocket can reach is:
h=u2R2GM−u2
The initial energy of the rocket consists of its kinetic energy and gravitational potential energy at the surface of the Earth.
KE=12mu2
- Potential Energy (PE):
PE=−GMmR
where G is the universal gravitational constant, M is the mass of the Earth, m is the mass of the rocket, and R is the radius of the Earth.
The total initial energy Ei at the surface of the Earth is:
Ei=KE+PE=12mu2−GMmR
At the maximum height h, the rocket will momentarily stop, so its kinetic energy will be zero. The potential energy at height h can be expressed as:
PE=−GMmR+h
According to the conservation of energy, the initial energy must equal the final energy:
Ei=Ef
Substituting the expressions for initial and final energy:
12mu2−GMmR=−GMmR+h
We can cancel m from the equation (assuming m≠0):
12u2−GMR=−GMR+h
Rearranging gives:
12u2=GMR−GMR+h
Finding a common denominator for the right side:
12u2=GM(R+h−R)R(R+h)=GMhR(R+h)
Now, we can solve for h:
h=u2R(R+h)2GM
This can be rearranged to isolate h:
h=u2R2GM−u2
Thus, the maximum height h that the rocket can reach is:
h=u2R2GM−u2
Topper's Solved these Questions
- GRAVITATIONBook:SL ARORAChapter:GRAVITATIONExercise:Problem From Competitive Examinations
Explore 14 Videos
- GRAVITATIONBook:SL ARORAChapter:GRAVITATIONExercise:Exercise
Explore 480 Videos
- FLUIDS IN MOTIONBook:SL ARORAChapter:FLUIDS IN MOTIONExercise:All Questions
Explore 117 Videos
- HEATBook:SL ARORAChapter:HEATExercise:Problem For Self Practice
Explore 72 Videos
Similar Questions
Two bodies of mass m1andm2 are initially at rest placed infinite distance apart. They are then allowed to move towards each other under mutual gravitational attaction. Show that their relative velocity of approach at separation r betweeen them is
v=√2G(m1+m2)r
View SolutionA sphere of mass 20 kg is attached by another sphere of mass 10 kg when their centres are 20 cm apart , with a force of 3.3×10−7N . Calculate the constant of gravitation .
View SolutionThe relative velocity of two parallel layers of water is 8 cm/sec. If the perpendicular distance between the layers is 0.1 cm, then velocity gradient will be
View SolutionA faulty thermometer reads 5∘C melting ice and 99∘C in steam. Find the correct temperature in .∘F when this faulty thermometer reads 52∘C.
View SolutionA rocket is launched vertically from the surface of earth with an initial velocity v . How far above the surface of earth it will go? Neglect the air resistance.
View SolutionThe escape velocity of a rocket launched from the surface of the earth
View SolutionA rocket is launched vetically from the surface of the earth with an initial velocity of 10 kms^(-1) . How for above the surface of the earth would it go ? Radius of the earth =6400 km and g=9.8 ms^(-2) .
View SolutionA rocket is launched vertical from the surface of the earth of radius R with an initial speed v . If atmospheric resistance is neglected, then maximum height attained by the rocket is
View SolutionA rocket is fired vertically with a speed of 5kms^(-1) From the Earth surface . How far from the Earth does the rocked go , before returning back ?
View SolutionA rocket is launched upward from the earth surface whose velocity time graph shown in figure. Then maximum height attained by the rocket is :-
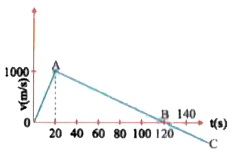
View SolutionA rocket is launched upward from the earth surface whose velocity time graph shown in figure. Then maximum height attained by the rocket is :-
View SolutionM द्रव्यमान का रॉकेट पृथ्वी की सतह से ऊर्ध्वाधर ऊपर की ओर v वेग से छोड़ा जाता है। यदि पृथ्वी की त्रिज्या R तथा वायु घर्षण नगण्य माना जाए, तो राकेट द्वारा पृथ्वी सतह से अधिकतम कितनी ऊँचाई तय की जाएगी?
View SolutionA rocket is launched striaght up from the surface of the earth the earth the minimum velocity with which it should coast is (Escape velocity on the surface of the earth is 11.2 kms^(-1) )
View SolutionR ব্যাসার্ধবিশিষ্ট পৃথিবীপৃষ্ঠ থেকে একটি রকেটকে v বেগে ওপরের দিকে ছোড়া হল। বায়ুর বাধাকে উপেক্ষা করলে রকেটটি যে সর্বাধিক উচ্চতা পর্যন্ত উঠতে পারে, তার মান
View SolutionA rocket is launched vertically from the surface of earth with an initial velocity v . How far above the surface of earth it will go? Neglect the air resistance.
View Solution
