A rod AB of length l is pivoted at an end A and freely rotated in a horizontal plane at an angular speed ω about a vertical axis passing through A. If coefficient of linear expansion of material of rod is α, find the percentage change in its angular velocity if temperature of system is incresed by ΔT
To solve the problem, we need to analyze the effects of temperature change on the angular velocity of a rotating rod. Here is a step-by-step solution:
Step 1: Understand the Moment of Inertia
The moment of inertia I of a rod of length l pivoted at one end is given by the formula:
I=13ml2
where m is the mass of the rod.
Step 2: Consider Linear Expansion
When the temperature of the rod increases by ΔT, the length of the rod changes due to thermal expansion. The change in length Δl can be expressed as:
Δl=αlΔT
where α is the coefficient of linear expansion.
Step 3: New Length of the Rod
The new length l′ of the rod after the temperature increase is:
l′=l+Δl=l+αlΔT=l(1+αΔT)
Step 4: New Moment of Inertia
Substituting the new length into the moment of inertia formula gives:
I′=13m(l′)2=13m(l(1+αΔT))2
Expanding this, we get:
I′=13ml2(1+2αΔT+(αΔT)2)
For small changes, we can neglect the (αΔT)2 term, so:
I′≈13ml2(1+2αΔT)
Step 5: Change in Moment of Inertia
The change in moment of inertia ΔI is:
ΔI=I′−I=13ml2(1+2αΔT)−13ml2=13ml2(2αΔT)
Step 6: Percentage Change in Moment of Inertia
The percentage change in moment of inertia is given by:
ΔII=13ml2(2αΔT)13ml2=2αΔT
Step 7: Conservation of Angular Momentum
According to the conservation of angular momentum:
Iω=constant
Thus,
Iω=I′ω′
From this, we can express the change in angular velocity Δω:
ΔI⋅ω+I⋅Δω=0
This leads to:
ΔII+Δωω=0
Substituting the percentage change in moment of inertia, we have:
2αΔT+Δωω=0
Thus,
Δωω=−2αΔT
Step 8: Percentage Change in Angular Velocity
To find the percentage change in angular velocity, we multiply by 100:
Percentage change=Δωω×100=−200αΔT
Final Answer
The percentage change in angular velocity is:
Percentage change=−200αΔT
The moment of inertia I of a rod of length l pivoted at one end is given by the formula:
I=13ml2
where m is the mass of the rod.
When the temperature of the rod increases by ΔT, the length of the rod changes due to thermal expansion. The change in length Δl can be expressed as:
Δl=αlΔT
where α is the coefficient of linear expansion.
The new length l′ of the rod after the temperature increase is:
l′=l+Δl=l+αlΔT=l(1+αΔT)
Substituting the new length into the moment of inertia formula gives:
I′=13m(l′)2=13m(l(1+αΔT))2
Expanding this, we get:
I′=13ml2(1+2αΔT+(αΔT)2)
For small changes, we can neglect the (αΔT)2 term, so:
I′≈13ml2(1+2αΔT)
The change in moment of inertia ΔI is:
ΔI=I′−I=13ml2(1+2αΔT)−13ml2=13ml2(2αΔT)
The percentage change in moment of inertia is given by:
ΔII=13ml2(2αΔT)13ml2=2αΔT
According to the conservation of angular momentum:
Iω=constant
Thus,
Iω=I′ω′
From this, we can express the change in angular velocity Δω:
ΔI⋅ω+I⋅Δω=0
This leads to:
ΔII+Δωω=0
Substituting the percentage change in moment of inertia, we have:
2αΔT+Δωω=0
Thus,
Δωω=−2αΔT
To find the percentage change in angular velocity, we multiply by 100:
Percentage change=Δωω×100=−200αΔT
The percentage change in angular velocity is:
Percentage change=−200αΔT
टॉपर्स ने हल किए ये सवाल
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Single Correct
Explore 148 Videos
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Multiple Correct
Explore 25 Videos
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Exercise 1.3
Explore 18 Videos
- BASIC MATHEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:BASIC MATHEMATICSExercise:Exercise 2.6
Explore 20 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
समान प्रश्न
The design of some physical instrument requires that there be a constant difference in length of 10 cm between an iron rod and a copper cylinder laid side by side at all temperature find their lengths
(αFe=11×106.∘C−1,αCu=17×10−6.∘C−1)
View SolutionDue to thermal expansion with rise in temperature:
View SolutionExplain why the surface of a lake freezes first.
View SolutionThe displacement of a particle is given by y=(6t2+3t+4)m, where t is in seconds. Calculate the instantaneous speed of the particle.
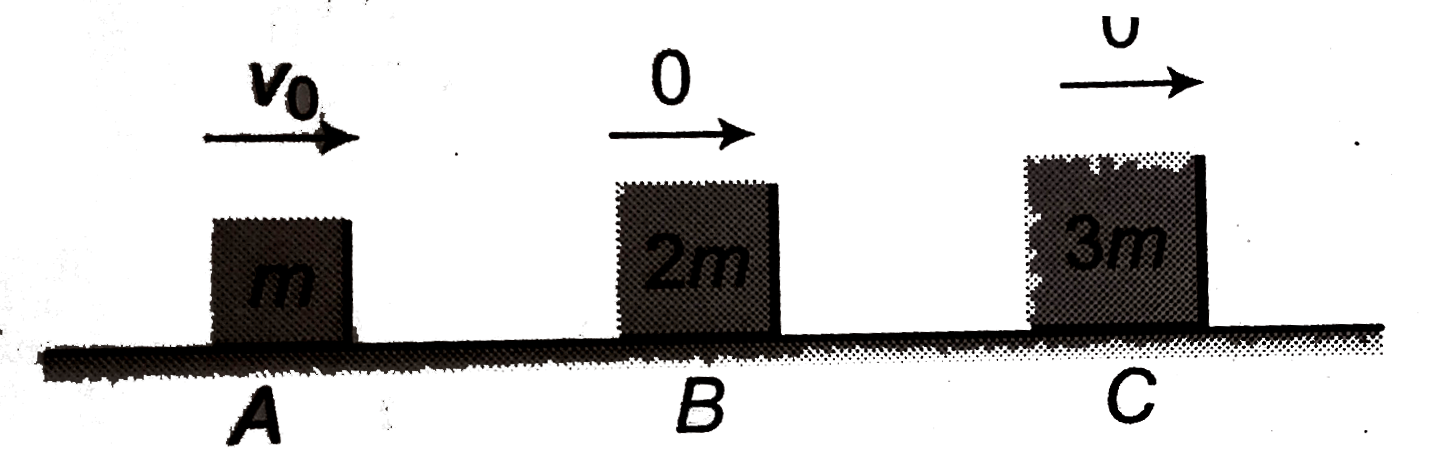
View SolutionThree objects A ,B and C are kept in a straight line on a smooth horizontal surface. These have masses m, 2m and 3m , respectively . The head - on elastic collision takes place between A and B and then B makes completely inelastic collision with C. All motions occur on the same straight line. The final speed of C will be
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA rod AB of length l is pivoted at an end A and freely rotated in a horizontal plane at an angular speed omega about a vertical axis passing through A. If coefficient of linear expansion of material of rod is alpha , find the percentage change in its angular velocity if temperature of system is incresed by DeltaT
View SolutionA uniform metal rod of length L and mass M is rotating about an axis passing throuth one of the ends perpendicular to the rod with angular speed ω. If the temperature increases by t∘C then the change in its angular velocity is proportional to which of the following ? (Coefficient of linear expansion of rod =α)
View SolutionA uniform cylindrical rod of mass m and length L is rotating with an angular velocity omega . The axis of rotation is perpendicular to its axis of symmetry and passes through one of its edge faces. If the room temperature increases by t and the coefficient of linear expansion is alpha , the change in its angular velocity is
View SolutionA rod PQ of length l=1 m is pivoted at an end P and is freely rotating in a horizontal plane at an angular speed omega about a vertical axis passing through P. If coefficient of linear expansion of material of rod is alpha=2xx10^(-4)//^(@)C then calculate percentage change in its angular speed (in multiple of 10^(-1)) if the temperature of system is increased by DeltaT=10^(@) C.
View SolutionA thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity omega in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is omega . The force applied on the rod by the pivot is
View SolutionA uniform metal rod of length L and mass M is rotating about an axis passing through one of the ends and perpendicular to the rod with angular speed omega. If th temperature increases by t^(@)C , then the change in its angular velocity is proportional to which of the following? (Coefficient of linear expansion of rod = a)
View SolutionThe temperature of uniform rod of length L having a coefficient of linear expansion αL is changed by ΔT . Calculate the new moment of inertia of the uniform rod about axis passing through its center and perpendicular to an axis of the rod.
View SolutionA rod AB of length l is pivoted at an end A and freely rotated in a horizontal plane at an angular speed ω about a vertical axis passing through A. If coefficient of linear expansion of material of rod is α, find the percentage change in its angular velocity if temperature of system is increased by ΔT.
View Solution
