A rod of length 1.05 m having negliaible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in fig. The cross-sectional area of wire A and B are 1mm2 and 2mm2, respectively . At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires. Given,
Ysteel=2×1011Nm−2andY−(aluminium)=7.0×1010N−2
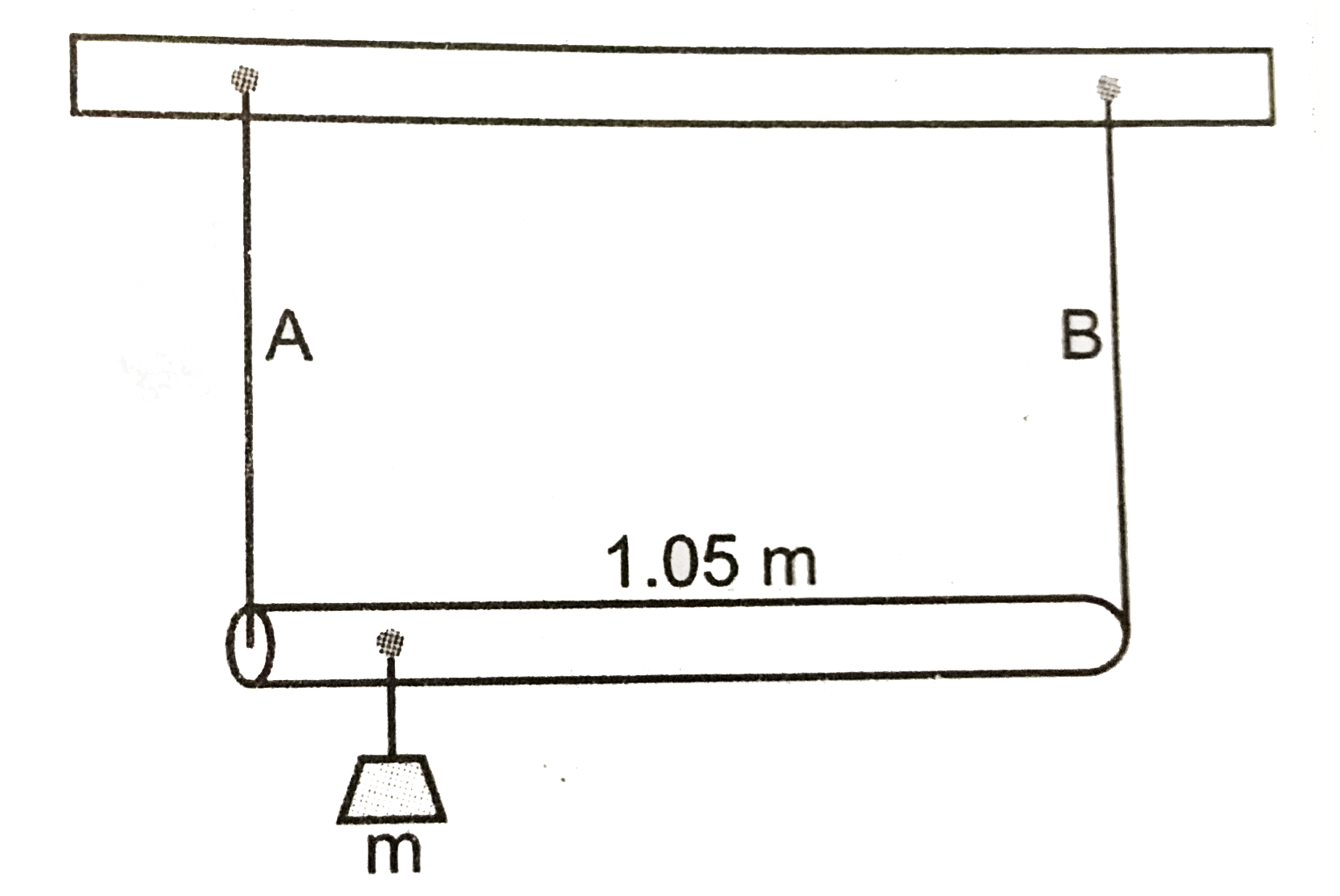
For steel wire A,l1=l,A1=1mm2,Y1=2×1011Nm−2
For aluminium wire B, l2=l,A2=2mm2,Y2=7×1010Nm−2
(a) Let mass m be suspeneded from the rod at distance x from the end where wire A is connected. let F1 and F2 be the tensions in two wires and there is equal stress in two wires, then
F1A1=F2A2orF1F2=A1A2=12 ..(i)
Taking moment of forces about point of suspension of mass from the rod, we have
F1x=F2(1.05−x)or1.05=xx=F1F2=12
or 2.10−2x=xorx=0.70m=70cm.
(b) Let mass m be suspeneded from the rod at distance x from the end where wire A is connected. let F1 and F2 be the tensions in two wires and there is equal stress in two wires, ie. ,
F1A1Y1=F2A2Y2 or F1F2=A1Y2A2Y2=12×2×10117×1010=107
As the rod is stationary, os F1x=F2(1.05−x)or1.05=xx=F1F2=107
or, 10x=7.35−7xorx=0.4324m=43.2cm.
Similar Questions
A rod of length 1 and negligible mass is suspended at its two ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in figure. The cross-sectional areas of wires A and B are 1.0 mm^(2) and 2.0 mm^(2) respectively. Y_("steel”) = 200 xx 10 ^(9) Nm ^(-2) and Y_("auminium”) = 70 xx 10 ^(9) Nm ^(-2)
View SolutionA rod of length 1.05 m having negliaible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in fig. The cross-sectional area of wire A and B are 1mm2 and 2mm2, respectively . At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires. Given,
Ysteel=2×1011Nm−2andY−(aluminium)=7.0×1010N−2

View SolutionAn iron rod B of length 1 m and mass 1 kg is suspended with help of two wires as shwon in figure. The area of cross-section of iron wire is 0.3 cm^(2) and of copper wire is 0.6cm^(2) . At what distance from iron wire a weight can be hung to produce equal stress in wires?
View SolutionA rod of length 1.05 m having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in Fig. 9.15. The cross-sectional areas of wires A and B are 1.0mm2and2.0mm2, respectively. At what point along the rod should a mass m be suspended in order to produce (a) equal stresses :
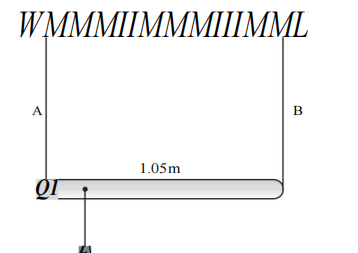
View SolutionA rod of length 1.05 m having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in Fig. 9.15. The cross-sectional areas of wires A and B are 1.0 mm^2 and 2.0 mm^2 , respectively. At what point along the rod should a mass m be suspended in order to produce equal strains in both steel and aluminium wires.:
View SolutionA rod of length 1.05 m having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal length as shown in the figure The cross sectional area of wires A and B are 1.0 mm^2 and 2.0 mm^2 , respectivley. AT wat point along the rod should a mass m be suspended in order to produce .equal stresses.
View SolutionA rod of length 1.05 m having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal length as shown in the figureThe cross sectional area of wires A and B are 1.0 mm^2 and 2.0 mm^2 , respectivley. AT wat point along the rod should a mass m be suspended in order to produce equal strains in both steel and aluminium wires?
View SolutionA rod of length l and negligible mass is suspended at its two ends by two wires of steel (wire A ) and aluminium (wire B) of equal length (shown in the figure) The cross-sectional areas of wires A and B are 1.0 mm^2 and 2.0 mm^2 , respectively. (Y_(AL) = 70 xx 10^9 N m^-2 and y _(steel) = 200 xx 10^9 N m^-2)
View Solution
