A small body A is fixed to the inside of a thin rigid hoop of radius R and mass equal to that of the body A. The hoop rolls without slipping over a horizontal plane, at the moments when the body A gets into the lower position, the centre of the hoop moves with velocity v0. At what values of v0 will the hoop move without bouncing?
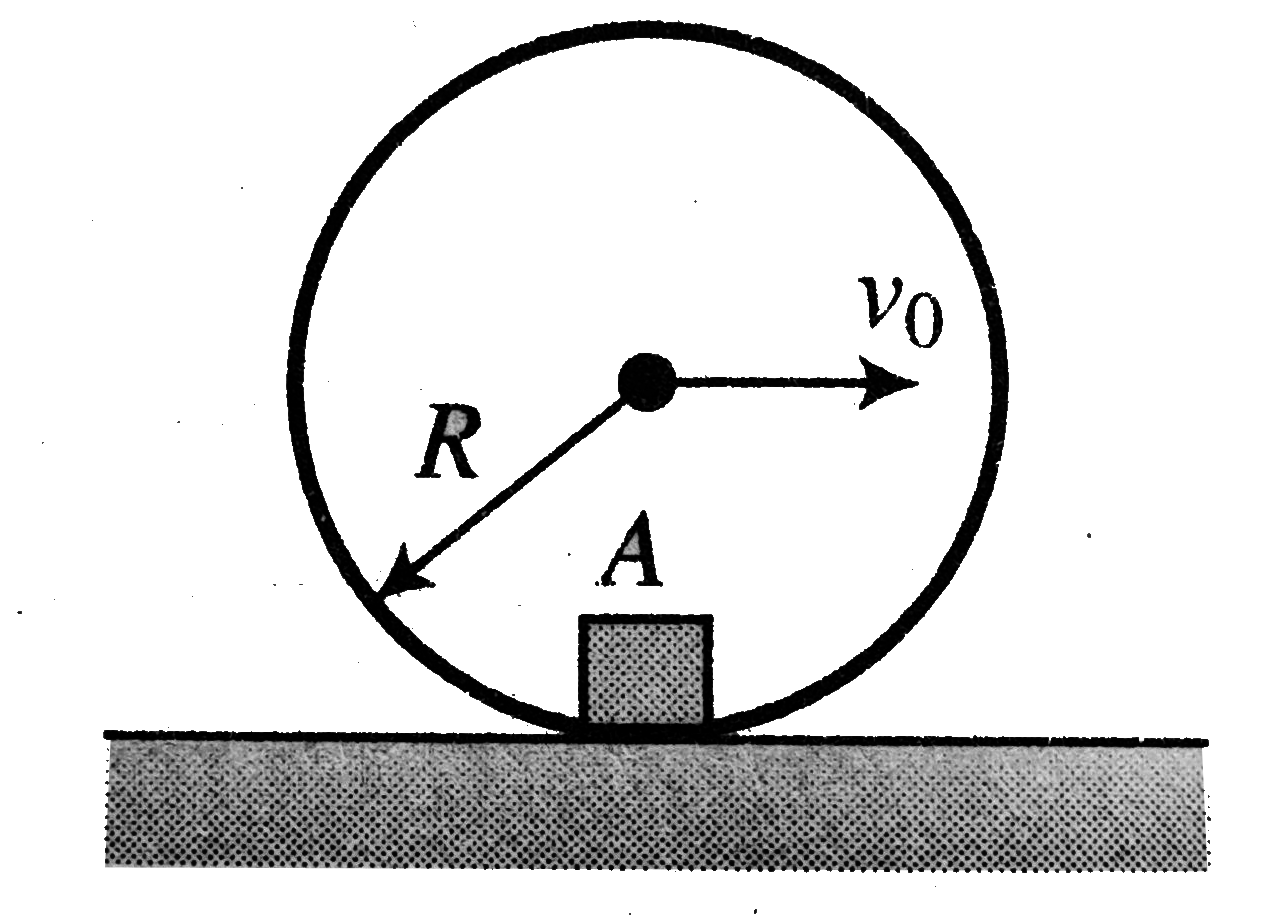
The correct Answer is:√8gR
One the hoop, the grond is giving a normal force R. Again the attached mass A is also giving a normal force N. Now value of R is changing as the attached body is changing its position. Value of R is minimum when the attached body is at the highest position in its circular motion. but this minimum value of R should also the greater than zero to prevent the hoop from bouncing.
Now consider FBD of the attached body
N+mg=mv2R.i
[where v=velocity of cenntre of mass of the hoop at tis moment. Again velocity of the body at its moment with respect to the hooop centre of mass =2v−v=v]
For the hoop
N+R=mg.....ii
From i and ii
mv2R−mg+R=mg⇒R=2mg=mv2R..........iii
R≥0,⇒v2≤2ghr........iv
Now conserving energying the reference rame of the ground:
mv2012mv20+12MR2ω20
=12mv2+12(mR2)ω2+12m(2v)2+2mgR
⇒ Putting v0=Rω0 and v=Rω:
v0=√8gR
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Single Correct
Explore 142 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Multiple Correct
Explore 26 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.4
Explore 13 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICS ENGLISHChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A uniform sphere of mass m and radius r rolls without sliding over a horizontal plane, rotating ahout a horizontal axle OA. In the process, the centre of the sphere moves with a veocity v along a circle of radius R. Find the kinetic energy of the sphere.
View Solution
A wheel is rolling without slipping on a horizontal plane with velocity v and acceleration a of centre of mass as shown in figure. Acceleration at
View SolutionA uniform solid cylinder of radius 'R' has a circular cut of radius R2 from the edge, Its mass is M. It is rolling wihtout slipping on a rough horizontal floor. When the cut part is at lowest position, centre of the disc is moving with horizontal velocity v. Choose the alternative:
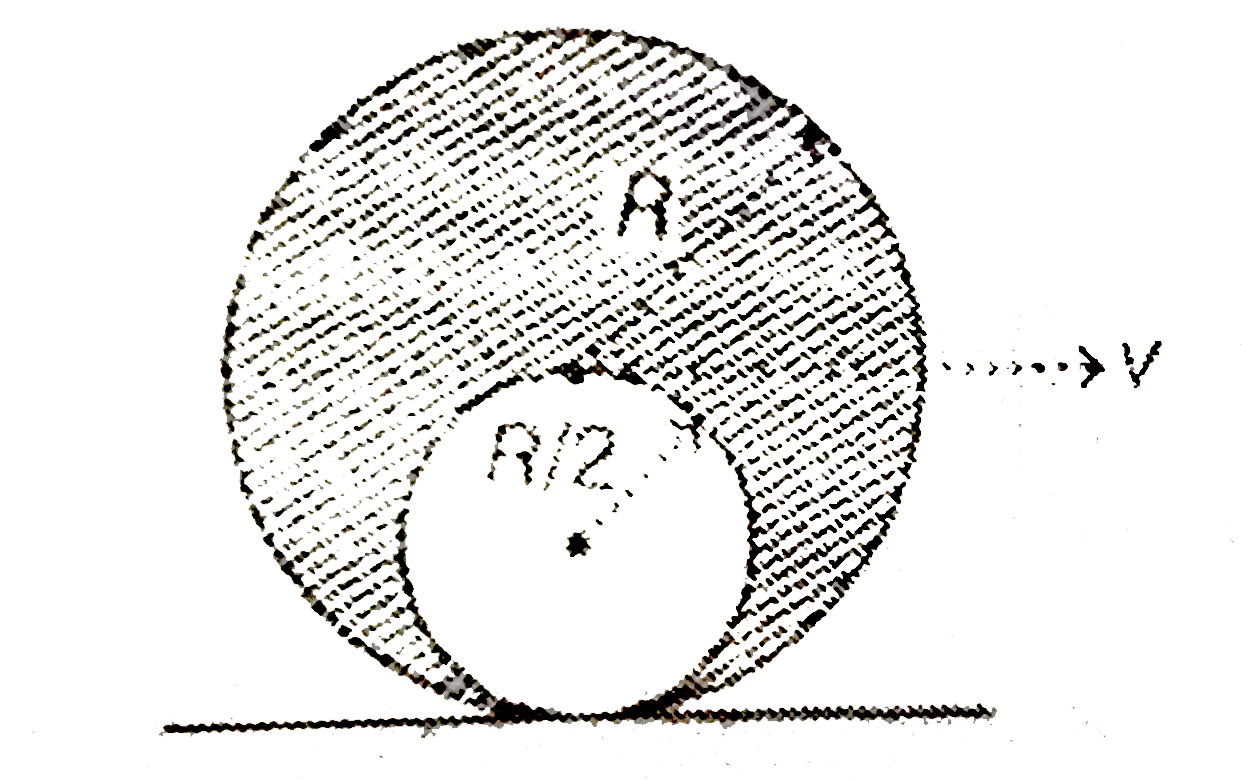
View SolutionThe centre of a wheel rolling without slipping on a plane surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre of wheel will be moving with speed
View SolutionA body of mass M moving with velocity V explodes into two equal parts. If one comes to rest and the other body moves with velocity v, what would be the value of v ?
View SolutionA round uniform body of radius R, mass M and moment of inertia 'I' rolls down (without slipping) and inclined plane making an angle θ with the horizontal. Then its acceleration is.
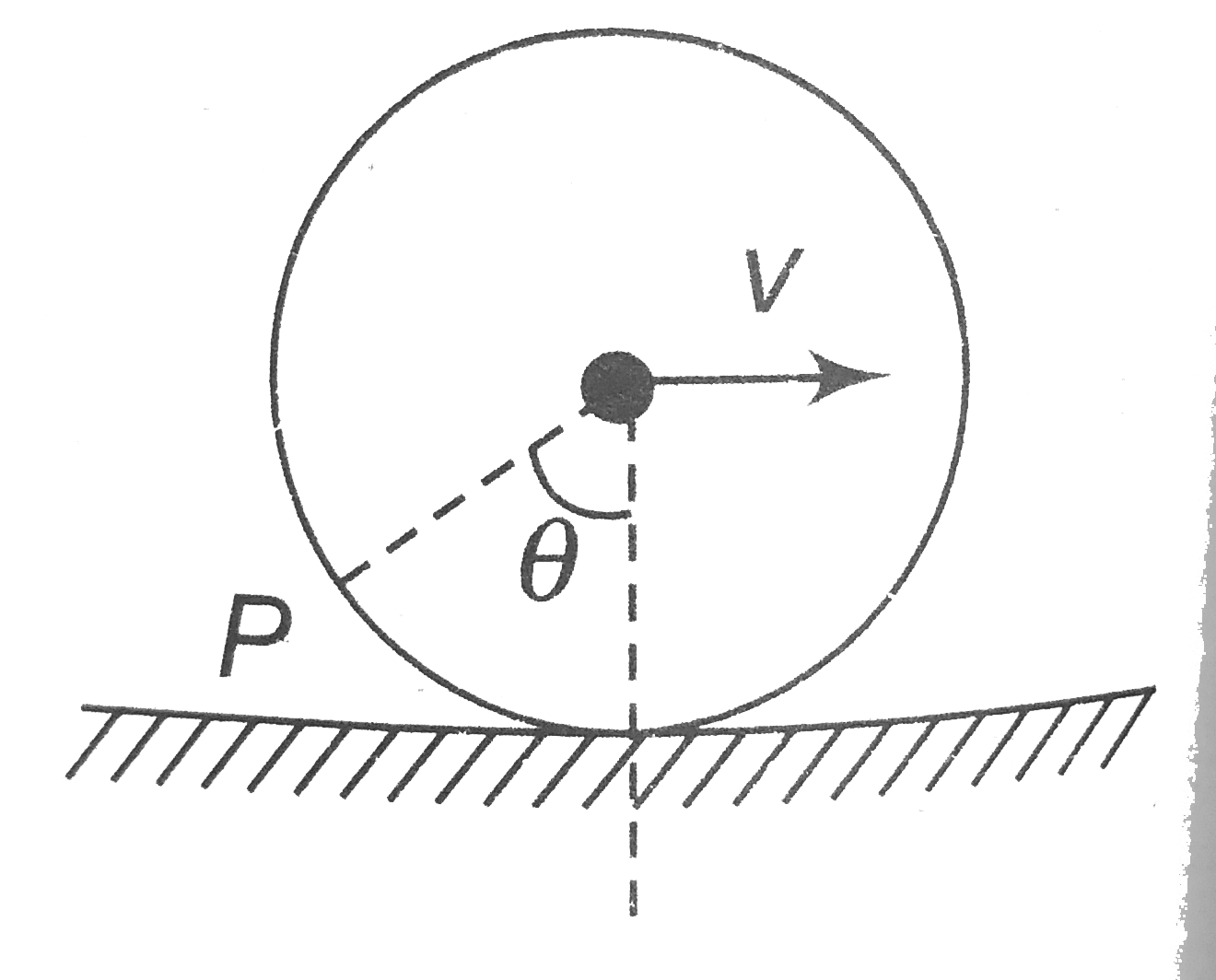
View SolutionA hoop rolls on a horizontal ground without slipping with linear speed v. Speed of a particle P on the circumference of the hoop at angle θ is :
View SolutionA uniform thin spherical shell of mass m and radius R rolls down without slipping over an inclined plane of angle θ with the horizontal. The ratio of rotational kinetic energy to the total kinetic energy of the shell will be
View SolutionA wheel of radius R=0.1m is rolling without slipping on a horizontal surface as shown in the firgure. Centre of the wheel moves with a constant speed √3m/s. The speed of the point P with respect to ground is

View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0 . We consider a point A on the surface of the disc. Then, the acceleration of point A is
View Solution
