A small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for

r<a
zero
14πε02qr2
−14πε06qr2
14πε0qr2
The correct Answer is:C
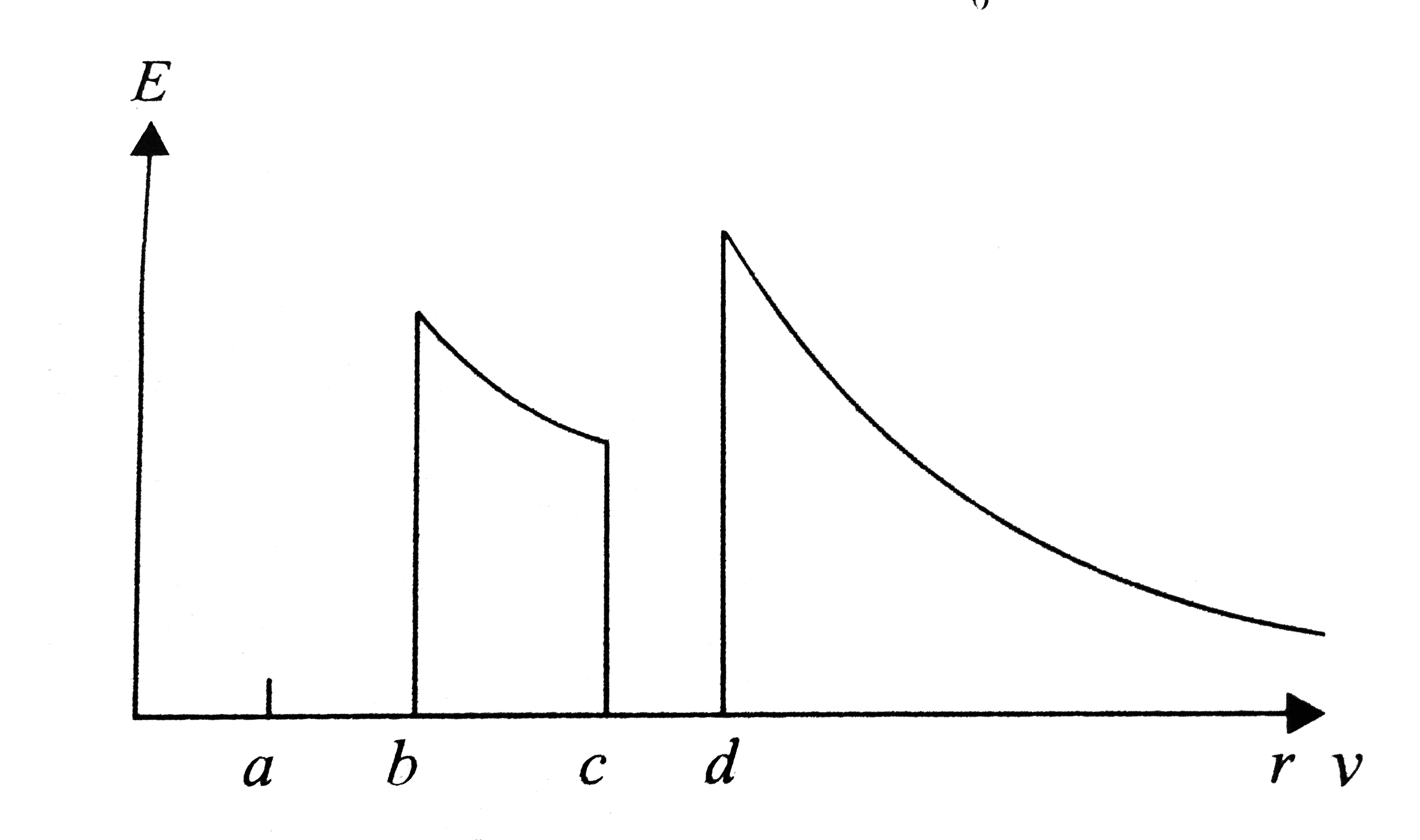
i. r<a.E=0, since Q=0 ( fig.S2.54)
ii. a<r<b.E=0 , since Q=0 .
iii. b<r<c. Since Q=+2q,E=14πε02qr2
iv. C lt r lt d. E = 0 , since Q=0.
v. r gt d. E = (1)/( 4 pi epsilon_(0)) ( 6 q)/( r^(2)),sinceQ = + 6 q.
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Subjective type
Explore 7 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Multiple Correct
Explore 8 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT AND CIRCUITExercise:Interger
Explore 8 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 15 Videos
Similar Questions
A suface has the area vector →A(2ˆi+3ˆj) what is the flux erof a uniform electric though the area if the field is a→E=4ˆiN/cand→E=4ˆkN/C ?
View SolutionElectric flux through a surface are 10m2 lying in the xy plane is (if→E=ˆi+√2ˆj+√3ˆkN/C)
View SolutionA 10 C charge is given to a conducting spherical shell, and a-3 C point charge is placed inside the shell. For this arrangement, find the correct statement(s).
View SolutionNine wires each of resistance R are connected to make a prism as shown in figure. Find the equivalent resistance of the arrangement across AB
View SolutionIn the figure shown a conducting sphere of inner radius 'a' and outer radius 'b' is given a charge Q. A point charge 'q' is placed in the cavity of this sphere at distance 'x'(<a) away from the centre. Find the electric field intensity and electric potentials at point P (outside the sphere) at distance r>b. Also find the electric potential at point C

View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for

r<a
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge + 2 q , and the outer shell has a total charge + 4 q . Calculate the electric field in terms of q and the distance r from the common center of the two shells for a lt r lt b
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for

b<r<c
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge + 2 q , and the outer shell has a total charge + 4 q . Calculate the electric field in terms of q and the distance r from the common center of the two shells for c lt r ltd
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge + 2 q , and the outer shell has a total charge + 4 q . Calculate the electric field in terms of q and the distance r from the common center of the two shells for r gt d
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge + 2 q , and the outer shell has a total charge + 4 q . Calculate the electric field in terms of q and the distance r from the common center of the two shells for The graph of the radial component of E as a function of r will be
View SolutionA point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell ?
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d. The inner shell has total charge +2q, and the outer shell has charge +4q. (K=(1)/(4piepsilon_(0)))

Find the electric field in terms of q and the distance r from the common centre of the two shells for (i) b<r<c (ii) c<r<d
View SolutionIn Fig a conducting spherical shell of inner radius .x. and outer radius .y. is concentric with a larger conducting spherical shell of inner radius .a. and outer radius .b.. Inner shell has a total charge +3Q and the outer shell has a charge +5Q. Let r be the distance of any point from the common centre O.

View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d ( as shown in Fig . 2.121). The inner shell has a total charge +2q, and the outer shell has a total charge +4q. Calculate the electric field in terms of q and the distance r from the common center of the two shells for

r<a
View Solution
