A solid cube of wood of side 2a and mass M is resting on a horizontal surface. The cube is constrained to rotate about an axis passing through D and perpendicular to face ABCD. A bullet of mass m and speed v is shot at a height of 4a/3 as shown in the figure. The bullet becomes embedded in the cube. Find the minimum value of v required to topple the cube. Assume m>>M.

Let ω be the angular velocity of cube just after collison about an axis passing through D. From conservation of the angular mometum about an axis passing through D.

mv(4a3)=ID.ω
Here ID=Icom+mr2
where r= perpedicular distance of axis of rotation passing through D from centre of mass (com) of the cube =√2a
or 4mva3=[M(42+4a212)+M(2a2)]ω
or 4mva3=83Ma2.ω
ω=12mvMa........i
The cube will topple if its COM is just able to reach in a vertical height h2 as shown in figure.

Hence applying conservation of mechanical energy
12IDω2=Mg(h2−h1) (∵ID=83Ma2)
or 12(83Ma2).{12mvMa}2=Mg(√2−1a
or 12(mM)2v2=ag(√2−1)
or v=Mm[3ag(√2−1)]12
Similar Questions
Knowledge Check
A solid cube of wood of side 2a and mass M is resting on a horizontal surface as shown in the figure. The cube is free to rotate about the fixed axis AB. A bullet of mass m (<<M) and speed v is shot horizontally at the face opposite to ABCD at a height 'h' above the surface to impart the cube an angular speed ωc so that the cube just topples over. Then ωc is (note : the moment of inertia of the cube about an axis perpendicular to the face and passing through the center of mass is 2Ma3/3)
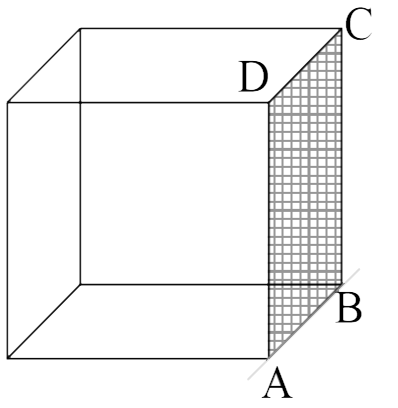 A√3gM/2maB√3g/4hC√3g(√2−1)/2aD√3g(√2−1)/4a
A√3gM/2maB√3g/4hC√3g(√2−1)/2aD√3g(√2−1)/4aA solid cube of wood of side 2a and mass M is resting on a horizontal surface as shown in the figure. The cube is free to rotate about a fixed axis AB. A bullet of mass m (<<M) and speed v is shot horizontally at the face opposite to ABCD at a height 4a/3 from the surface to impart the cube an angular speed ω. It strike the face and embeds in the cube. Then ωc is close to (note : the moment of inertia of the cube about an axis perpendicular to the face and passing through the center of mass is 2Ma2/3)
 AMv/maBMv/2maCmv/MaDmv/2Ma
AMv/maBMv/2maCmv/MaDmv/2MaA solid cube of side 2a and mass M, sliding on a smooth surface with velocity v0 , collides inelastically with the raised edge of the table:
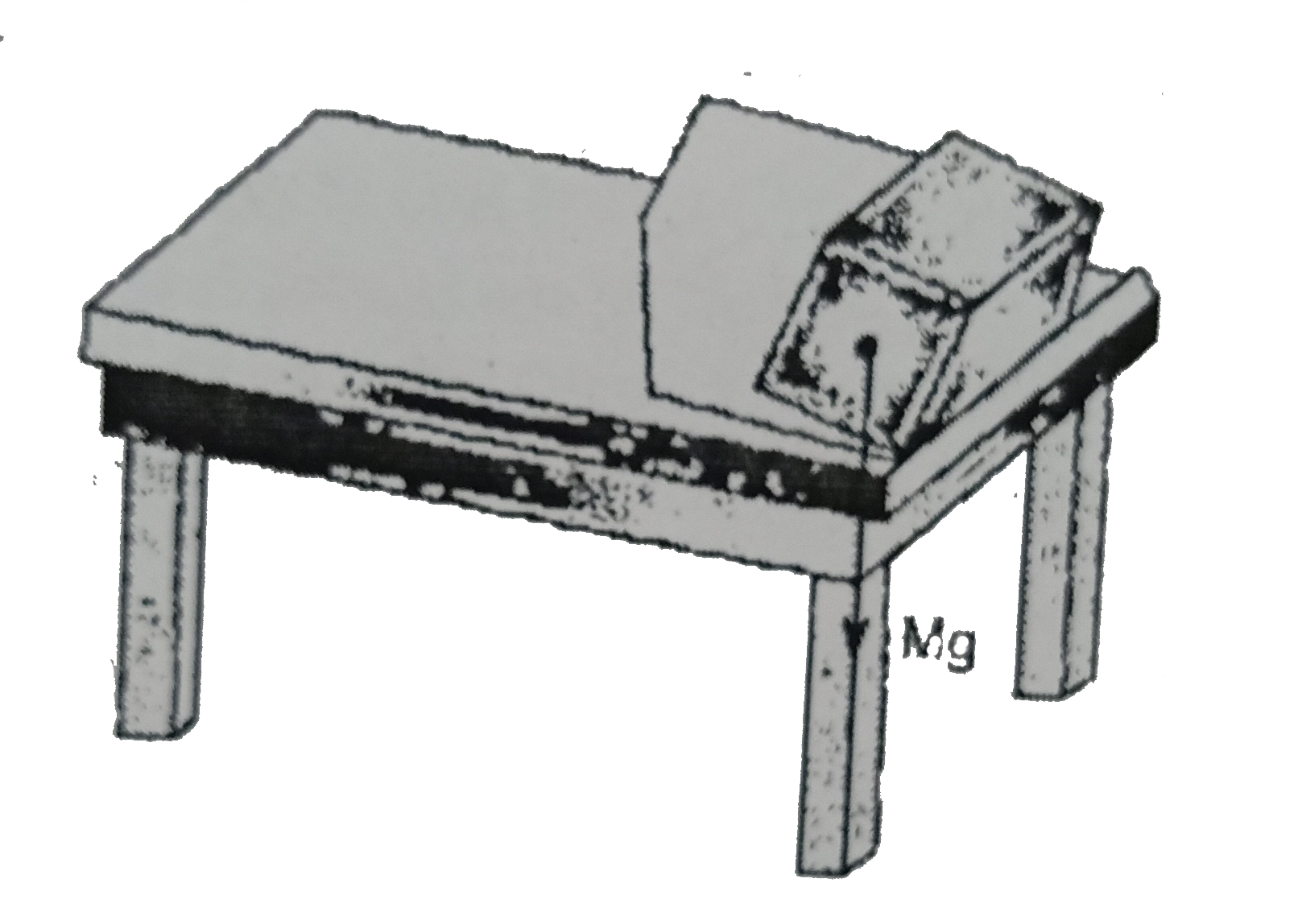 AMoment of inertia of cube about edge is 4Ma23BMoment of inertia of cube about edge is 8Ma23CMinimum value of v so that cube falls off the table is √1.19gDEnergy of system is conserved
AMoment of inertia of cube about edge is 4Ma23BMoment of inertia of cube about edge is 8Ma23CMinimum value of v so that cube falls off the table is √1.19gDEnergy of system is conserved
Figure shows a cubical wooden block of side length a and mass M which is resting over a horizontal surface and constrained to rotate about its right lower edge D. A bullet of mass m moving horizontally, directly towards its centre with velocity v strikes and gets embedded in it. During subsequent motion the block just topples, calculate v. Assume m<<M.
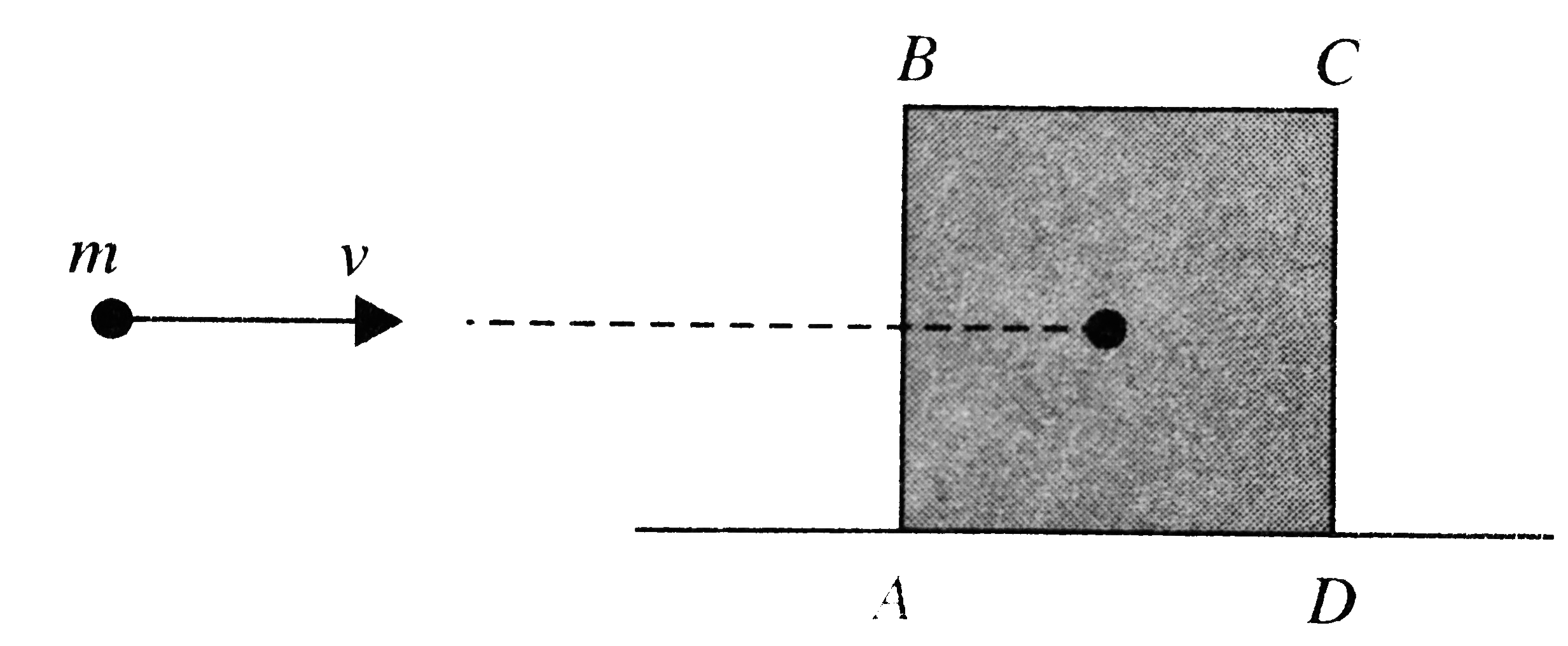
View SolutionFigure shows a cubical wooden block of side length a and mass M which is resting over a horizontal surface and constrained to rotate about its right lower edge D. A bullet of mass m moving horizontally, directly towards its centre with velocity v strikes and gets embedded in it. During subsequent motion the block just topples, calculate v. Assume m<<M.

View SolutionThe moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View SolutionThe moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View SolutionFrom a solid sphere of M and radius R a cube of maximum possible volume is cut. Moment of inertia of cube about an axis passing through its centre and perpendiular to one of its faces is:
View Solution


