A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if
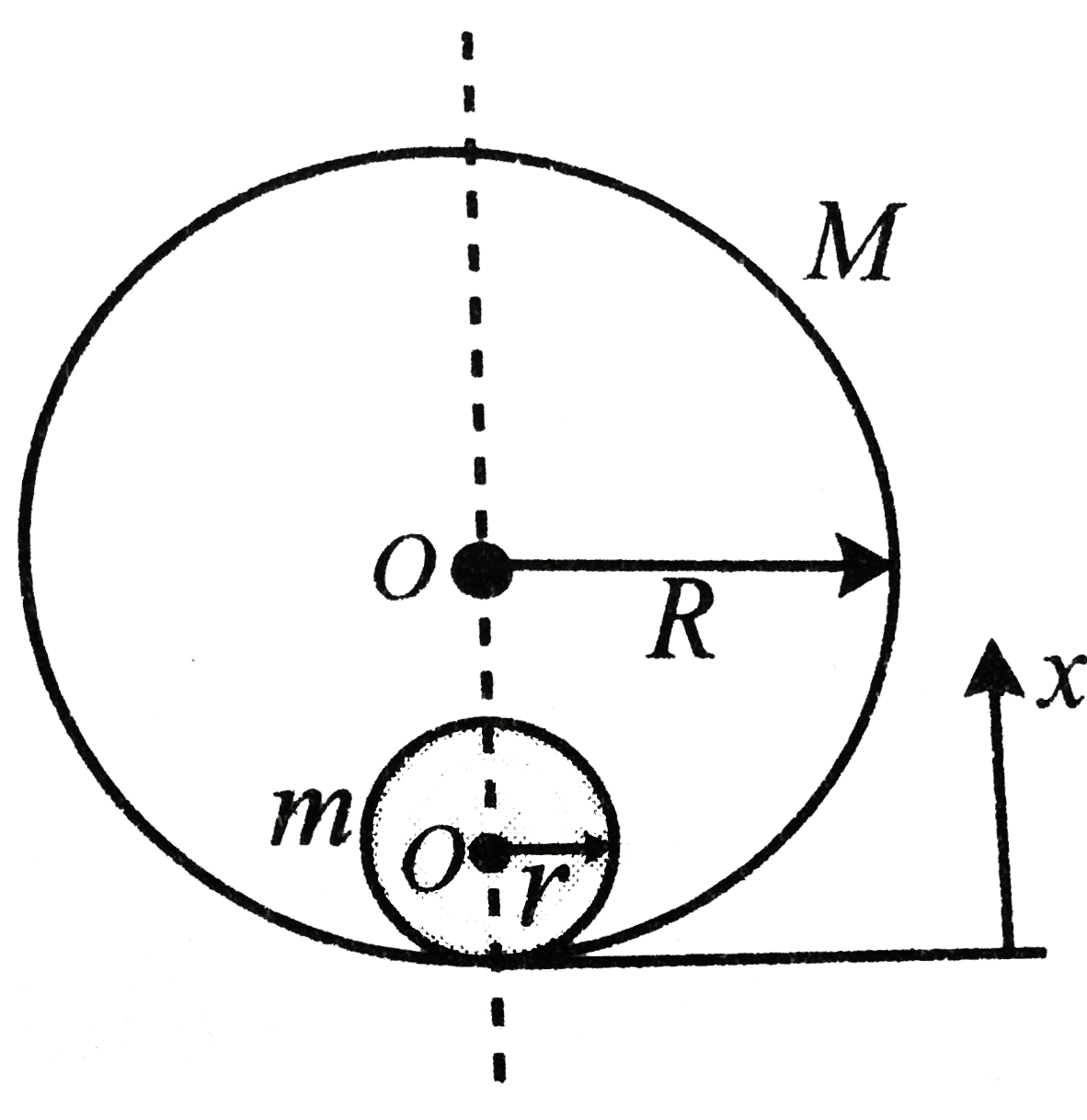
2r<x<2R
Gmm'(2r−x)2r3
Gmm'(x−r)2r3
Gmm'(x−r)r3
Gmm'(2x−r)r3
The correct Answer is:C
When 2r<x<2R 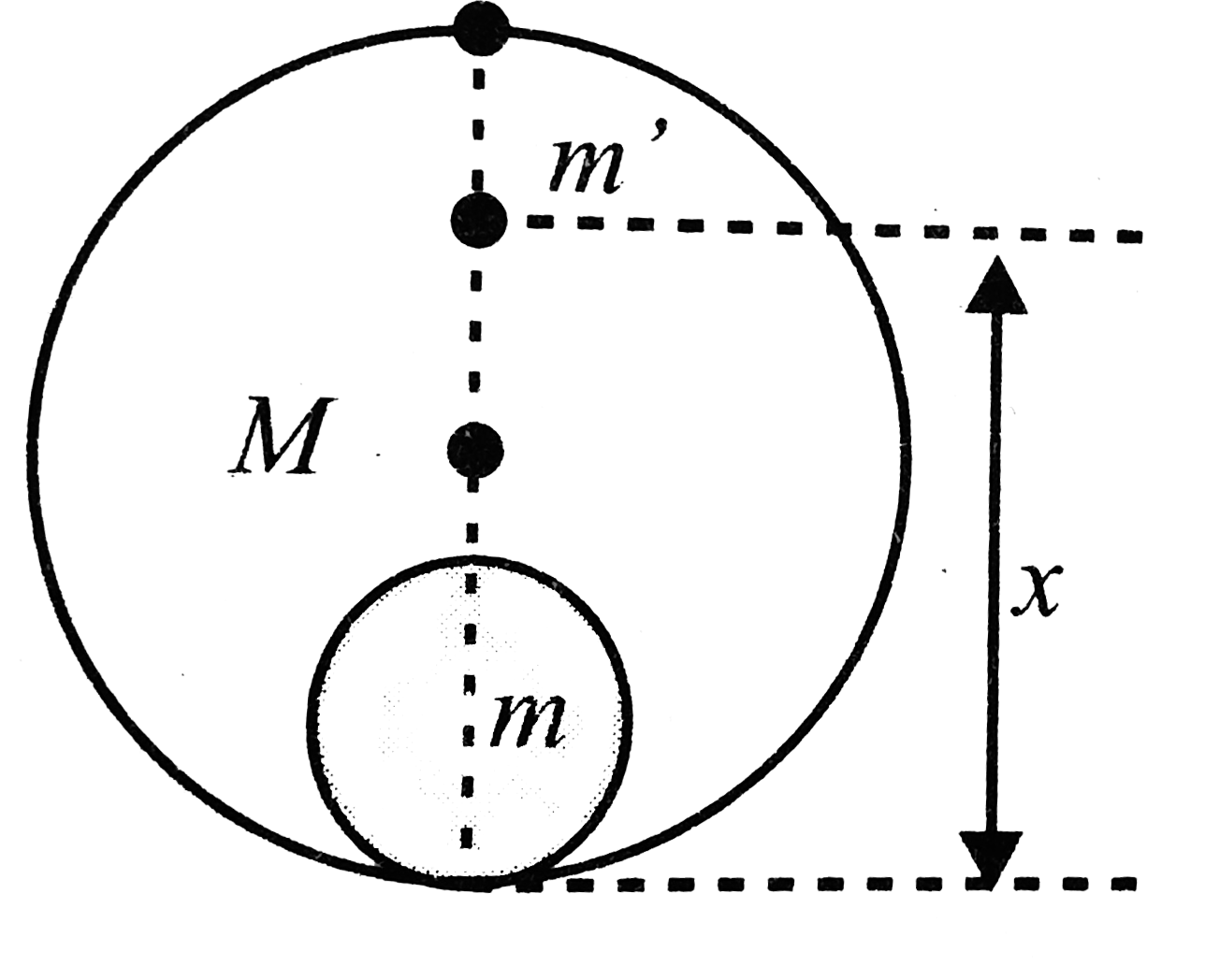
then the force will be due to sphere only.
F=Gmm'(x−r)2
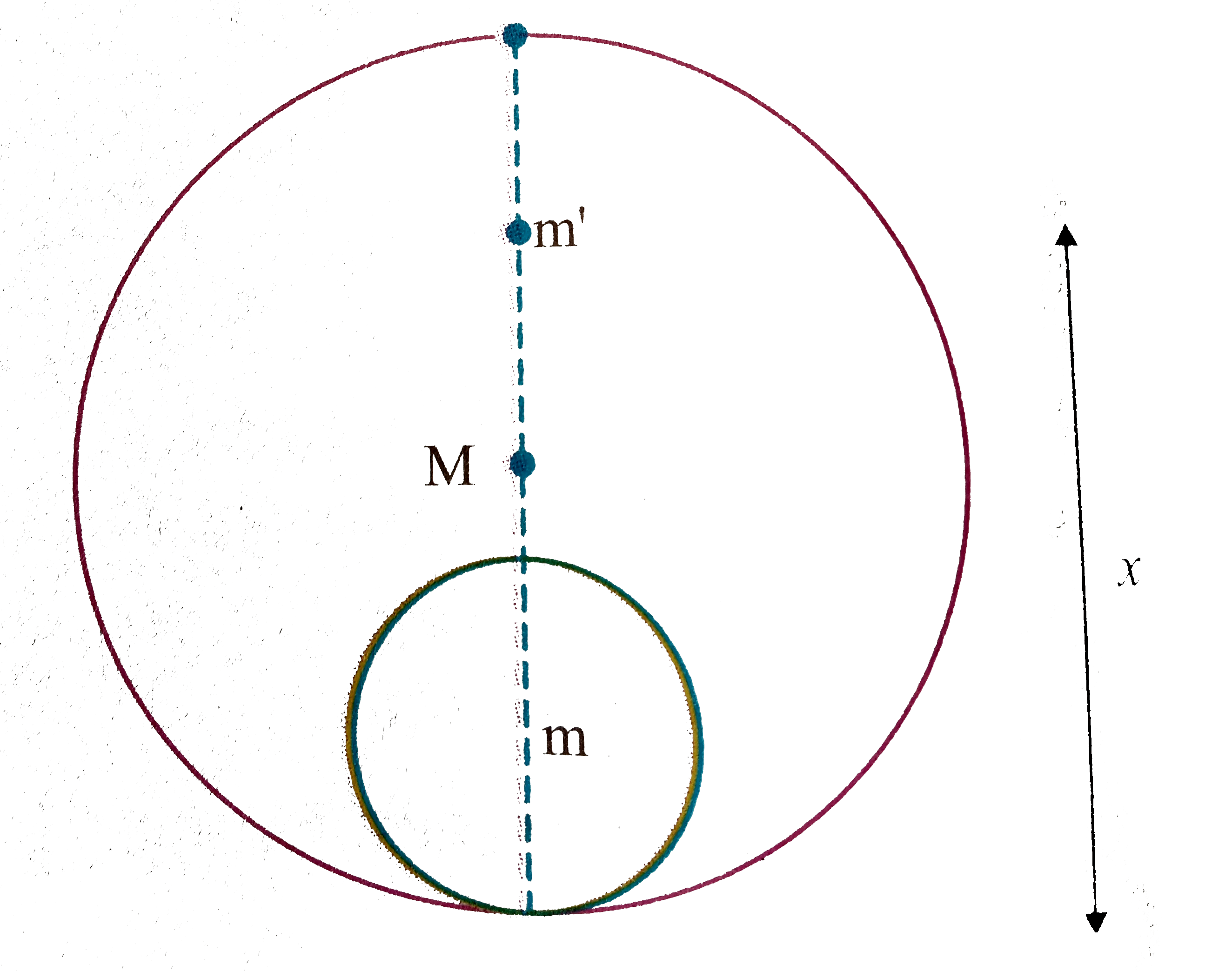
When x>2R. 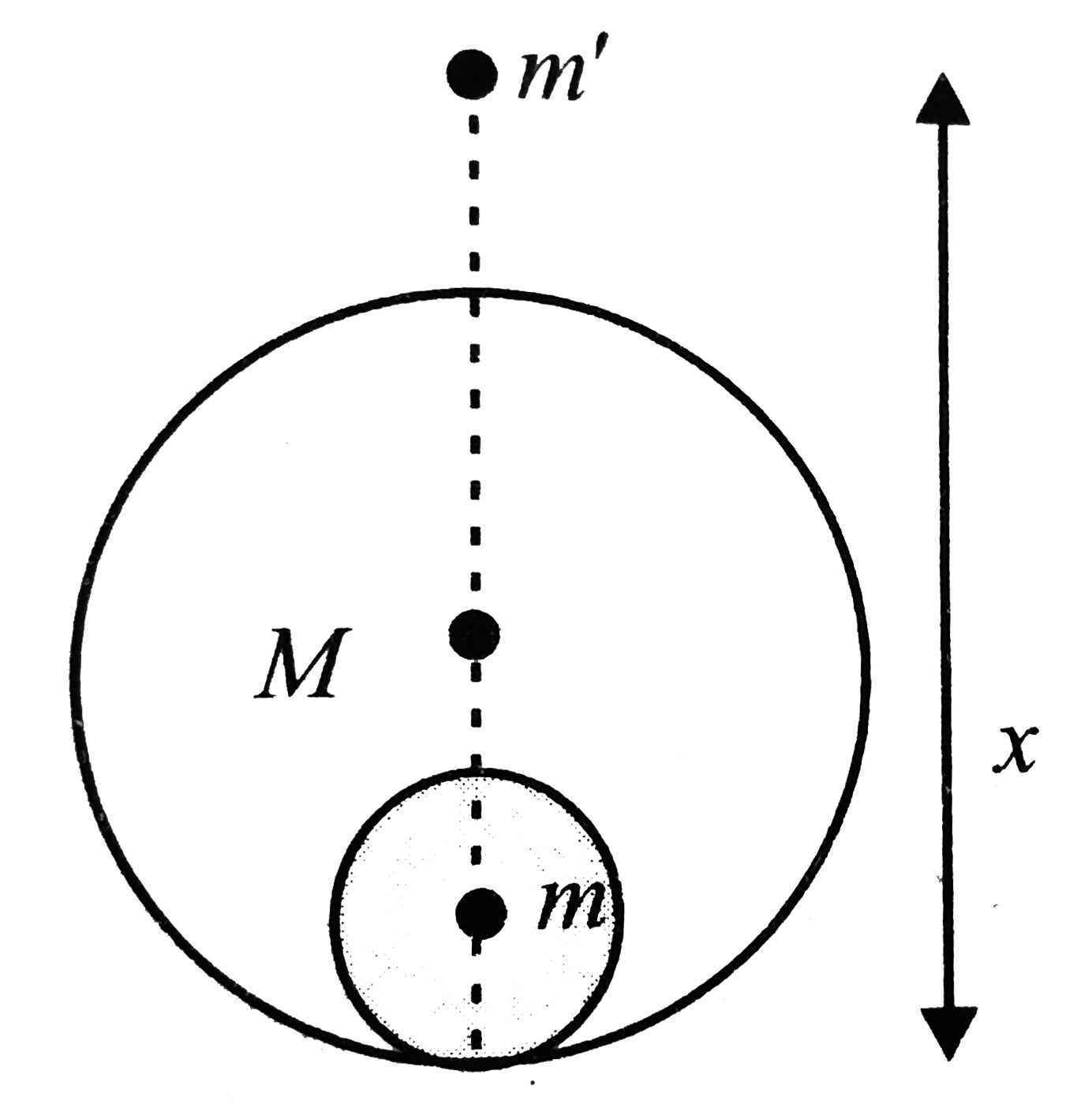
the sphere and the shell both will contribute to the
fsphere=GMm'(x−r)2
Fshell=GMm'(x−R)2
F=GMm'(x−R)2+GMm'(x−r)2
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Integer
5 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Fill In The Blanks
5 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning
13 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Video
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
A particle of mass m is subjected to an attractive central force of magnitude k/r2, k being a constant. If at the instant when the particle is at an extreme position in its closed orbit, at a distance a from the centre of force, its speed is (k/2ma), if the distance of other extreme position is b. Then a/b is
View SolutionAccording to Kepler's second law, the radius vector to a planet from the Sun sweeps out equal areas in equal intervals of time. This law is a consequence of the conservation of ______________.
View SolutionStatement 1: The value of escape velocity from the surface of earth at 30∘ and 60∘ is v1=2ve,v2=2/3ve.
Statement II: The value of escape velocity is independent of angle of projection.

View SolutionA cyclindrical vessel of height 500 mm has an orifice (small hole) at its bottom. The orifice is initially closed any water is filled in ti upto height H.Now the top is completely sealed with a cap and the orifice at the bottom is opened .Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. The fall in height (in mm) of water level due to opening of the orifice is [ Take atmospheric pressure = 1.0×105Nm2, density of water = 1000kgm3. Neglect any effect of surface tension.]
View SolutionA man in a lift ascending with an upward acceleration a throws a ball vertically upwards with a velocity v with respect to himself and catches it after t1 seconds. After wards when the lift is descending with the same acceleration a acting downwards the man again throws the ball vertically upwards with the same velocity with respect to him and catches it after t2 seconds?
View Solutiona solid sphere of mass m and radius r is plced nside as hollow thin spherical shell of mass and M and radius R as shown in figure. A particle of mas m is placed on tehline joining the tow centres ast a distance x from the point of contct of th sphere and teh shell. Findn teh mgnitude fo the resultant gravitational force on this particle due to the sphere and the shell if a. r<x<2r,b.2r<x<2Randc.x>2R.

View SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

r<x<2r
View SolutionA point mass m is placed inside a spherical shell of radius R and mass M at a distance R2 form the centre of the shell. The gravitational force exerted by the shell on the point mass is
View SolutionA solid sphere of mass m radius r is placed inside a hollow thin spherical shell of mass M and radius 2r as shown in figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if
2r<x<2R
View SolutionA solid sphere of mass m radius r is placed inside a hollow thin spherical shell of mass M and radius 2r as shown in figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

x>2R
View SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in figure−6.30. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this - particle due to the sphere and the shell if (a) r<x<2r,(b)2r<x<2Rand(c)x>2R.
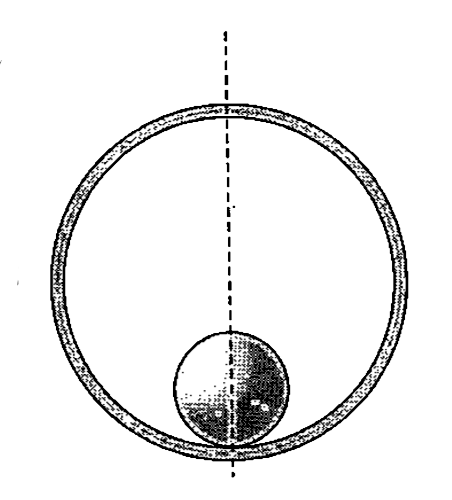
View Solutionचित्र 20.E2 में m द्रव्यमान एवं r त्रिज्या का एक ठोस गोला M द्रव्यमान एवं R त्रिज्या वाले एक पतले गोलीय कोश में रखा हुआ है। दोनो के केद्रो को मिलानेवाली रेखा पर एवं गोले तथा कोश के संपर्क- बिंदु से x दूरी पर m द्रव्यमान का एक कण रखा गया है। इस कण पर गोले तथा कोश के कारण लगनेवाले परिणामी गुरूत्वीय बल का परिमाण ज्ञात करें यदि।
(a)r<x<2r,(b)2r<x<2R तथा (c)x>2R

View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of mass 2M and radius R. The gravitational potential on the surface of the shell is:
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of mass 2M and radius R. The gravitational potential on the surface of the shell is
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of mass 2M and radius R. The gravitational potential on the surface of the shell is
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of mass 2M and radius R. The gravitational potential on the surface of the shell is
View Solution

