
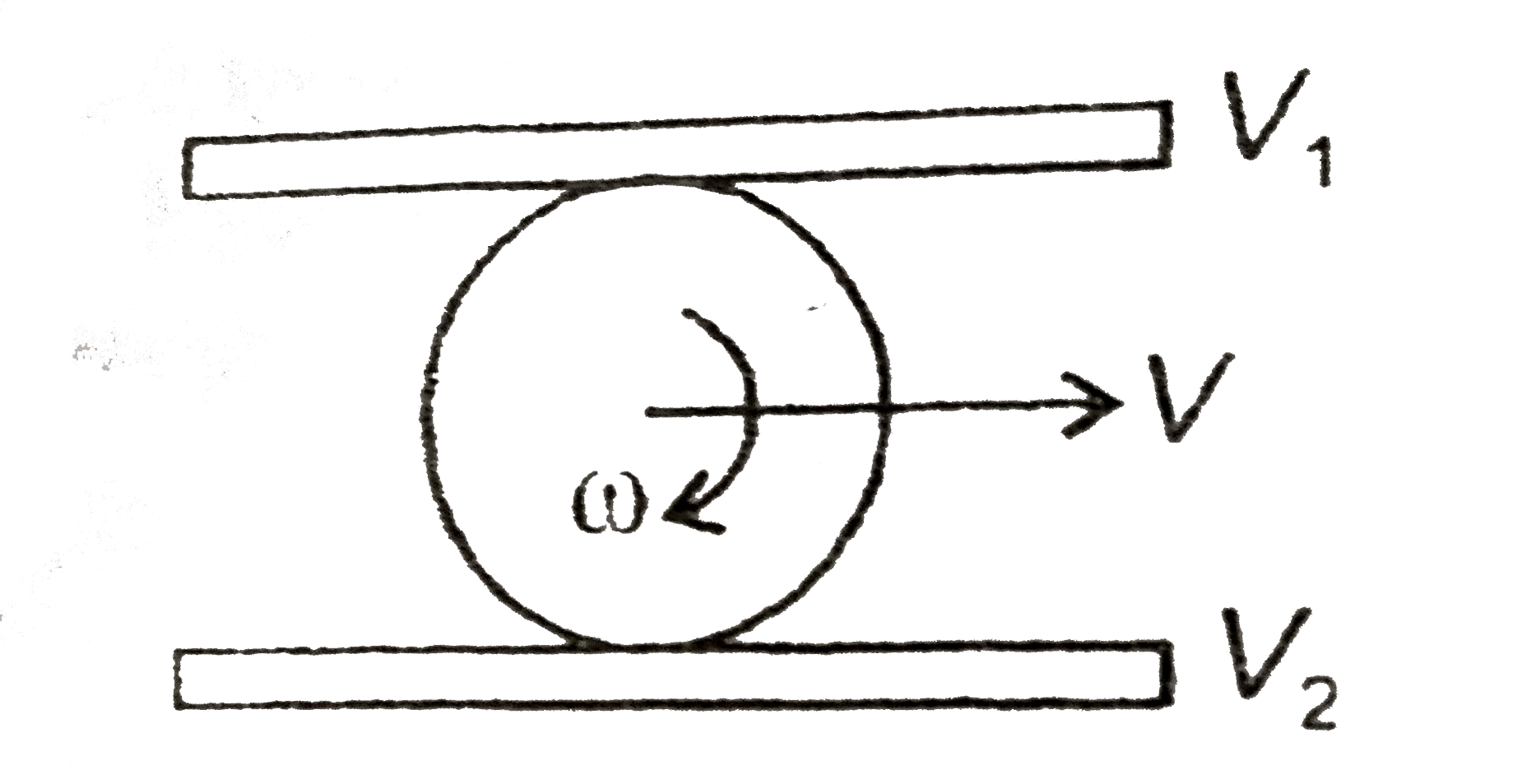
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
L=mvr⊥+Icω
=mvR+(25mR2)(vR)
=75mvR
this is clockwise, or along negative z-axis
∴L=(−75mvR)ˆk
Similar Questions
The ratio of the acceleration for a solid sphere (mass m and radius R) rolling down an incline of angle θ without slipping and slipping down the incline without rolling is,
View SolutionThe ratio of the accelerations for a solid sphere (mass .m. and radius .R.) rolling down and incline of angle or without slipping and slipping down the incline without rolling is
View SolutionThe ratio of the accelerations for a solid sphere (mass m and radius R) rolling down an incline of angle theta without slipping and slipping down the incline without rolling is
View Solution
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View SolutionThe ratio of the accelerations for a solid sphere (mass m,andradiusR) rolling down an incline of angle θ without slipping, and slipping down the incline without rolling is
View SolutionA sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If mass of the sphere is m and its radius be R, then the angular momentum of the sphere about the point of contact is.
View SolutionThe ratio of the accelerations for a solid sphere (mass 'm' and radius 'R') rolling down an incline of angle θ without slipping and slipping down the incline without rolling is
View SolutionA sphere of radius R rolls without slipping between two planks as shown in figure. Find
(a) Speed of centre of sphere
(b) Angular velocity of the sphere
View Solution
