A spherical capacitor consists of two concentric spherical shells of outer radius r1 and inner radius r2, held in position by suitable insulating supports. calculate the capacitance of this spherical capacitor.
4πε0r1r2r1−r2
4πε0−(r2−r1)r1r2
r1r24πε0(r2−r1)
(r1−r2)4πε0r1r2
The correct Answer is:A
To calculate the capacitance of a spherical capacitor consisting of two concentric spherical shells with outer radius r1 and inner radius r2, we can follow these steps:
1. Understanding the Setup:
- We have two concentric spherical shells: the inner shell (radius r2) and the outer shell (radius r1).
- The inner shell is given a positive charge +Q, which distributes uniformly over its surface.
2. Induction Effect:
- The positive charge on the inner shell induces a negative charge −Q on the inner surface of the outer shell (radius r1).
- Consequently, the outer surface of the outer shell will have a charge of +Q (since the outer shell is grounded, it will lose some positive charge to the ground).
3. Electric Field Calculation:
- The electric field E in the region between the two shells (from r2 to r1) can be calculated using Gauss's law. The electric field due to a uniformly charged sphere at a distance r (where r2<r<r1) is given by:
E=14πϵ0⋅Qr2
4. Potential Difference Calculation:
- The potential difference V between the inner shell (at r2) and the outer shell (at r1) is given by:
V=VA−VB=−∫r1r2Edr
- Substituting the expression for E:
V=−∫r1r214πϵ0⋅Qr2dr
- Evaluating the integral:
V=−Q4πϵ0(−1r)r1r2=Q4πϵ0(1r2−1r1)
5. Capacitance Calculation:
- The capacitance C of the spherical capacitor is defined as:
C=QV
- Substituting the expression for V:
C=QQ4πϵ0(1r2−1r1)=4πϵ0(1r2−1r1)
- Simplifying further:
C=4πϵ0r1r2r1−r2
Final Result:
The capacitance of the spherical capacitor is given by:
C=4πϵ0r1r2r1−r2
- We have two concentric spherical shells: the inner shell (radius r2) and the outer shell (radius r1).
- The inner shell is given a positive charge +Q, which distributes uniformly over its surface.
- The positive charge on the inner shell induces a negative charge −Q on the inner surface of the outer shell (radius r1).
- Consequently, the outer surface of the outer shell will have a charge of +Q (since the outer shell is grounded, it will lose some positive charge to the ground).
- The electric field E in the region between the two shells (from r2 to r1) can be calculated using Gauss's law. The electric field due to a uniformly charged sphere at a distance r (where r2<r<r1) is given by:
E=14πϵ0⋅Qr2
- The potential difference V between the inner shell (at r2) and the outer shell (at r1) is given by:
V=VA−VB=−∫r1r2Edr
- Substituting the expression for E:
V=−∫r1r214πϵ0⋅Qr2dr
- Evaluating the integral:
V=−Q4πϵ0(−1r)r1r2=Q4πϵ0(1r2−1r1)
- The capacitance C of the spherical capacitor is defined as:
C=QV
- Substituting the expression for V:
C=QQ4πϵ0(1r2−1r1)=4πϵ0(1r2−1r1)
- Simplifying further:
C=4πϵ0r1r2r1−r2
The capacitance of the spherical capacitor is given by:
C=4πϵ0r1r2r1−r2
Similar Questions
A spherical capacitor consists of two concentric spherical conductors, held in position by suitable insulating supports. Show that the capacitance of this spherical capacitor is given by C=4π∈0r1r2r1−r2,
Where r1andr2 are radial of outer and inner spheres respectively.
View SolutionThe capacitance of two concentric spherical shells of radii R1 and R2(R2>R1) is
View SolutionTwo concentric metallic spherical shells are given positive charges . Then
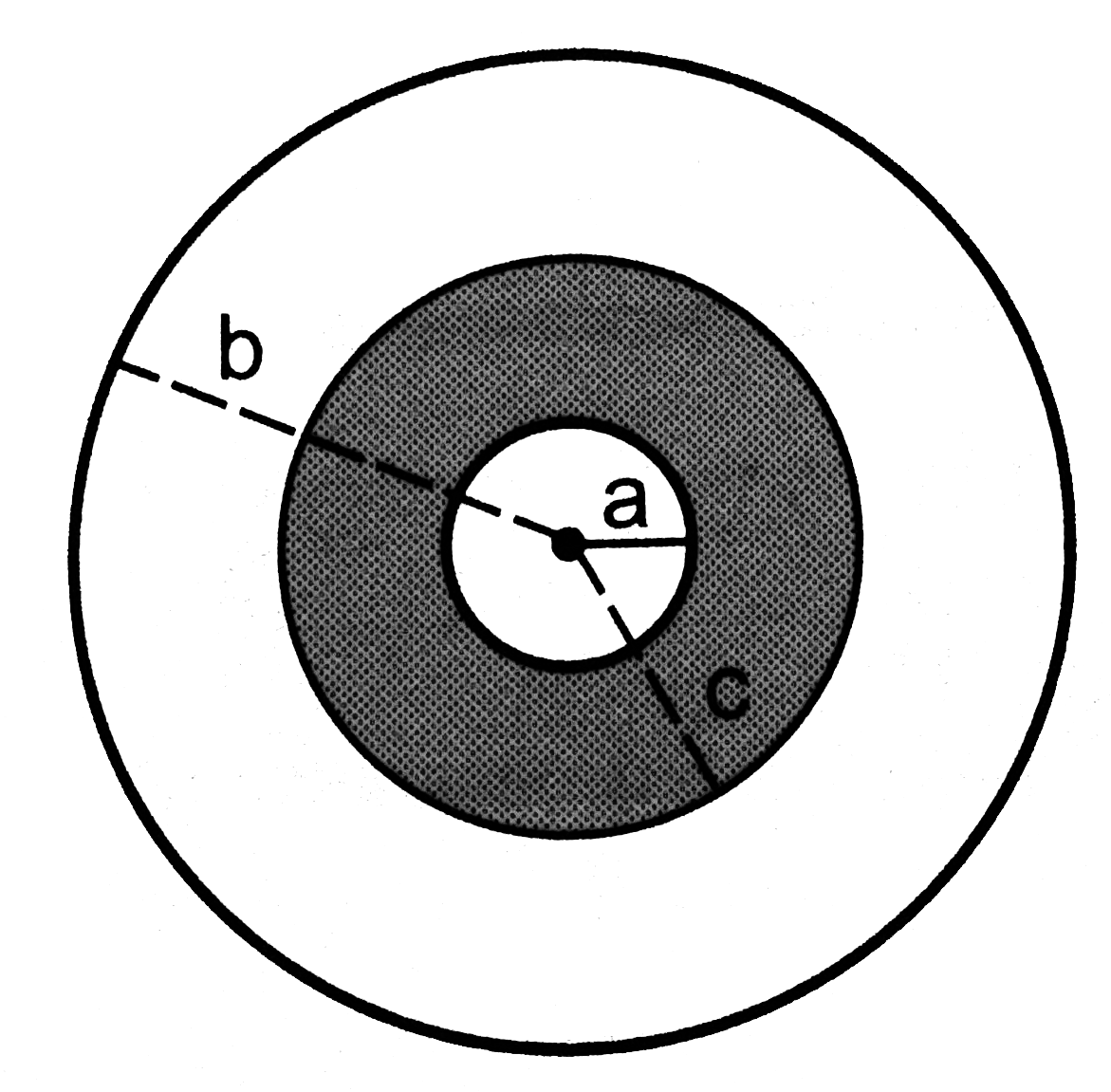
View SolutionA sphercial capacitor is made of two conducting spherical shells of radii a and b.The space between the shells is filled with a dielectric constant Kup to a radius c as shown in figure. Calculate the capacitance .
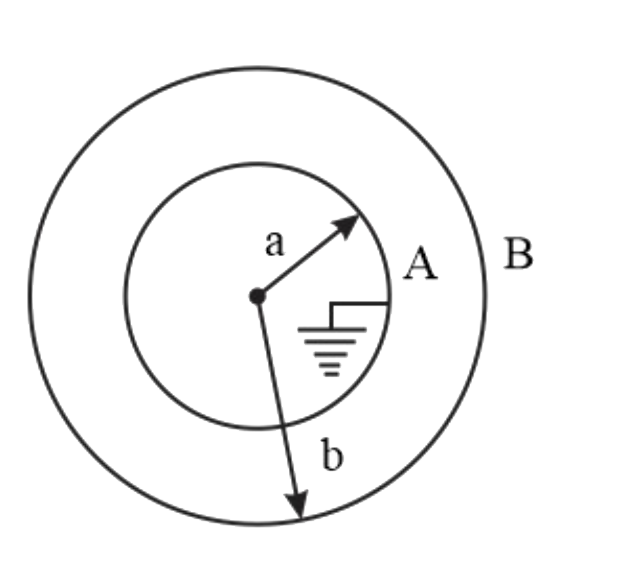
View SolutionThe equivalent capacitance between A and B, where two concentric spherical shells having radius a and b are connected as shown in the figure.
View SolutionA point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View SolutionA point charge Q is placed inside a conducting spherical shell of inner radius 3R and outer radius 5R at a distance R from the centre of the shell. The electric potential at the centre of the shell will be
View SolutionA point charge q is placed at a distance of r from the centre O of an uncharged spherical shell of inner radius R and outer radius 2R.The distance r<R.The electric potential at the centre of the shell will be

View SolutionA conducting sphere of radius R and a concentric thick spherical shell of inner radius 2R and outer radius 3R is shown in figure. A charge +10Q is given to the shell and inner sphere is earthed. Then charge on inner sphere is

View SolutionA point charge q is placed at a distance of r from the centre O of an uncharged spherical shell of inner radius R and outer radius 2R. The electric potential at the centre of the shell will be

View Solution
