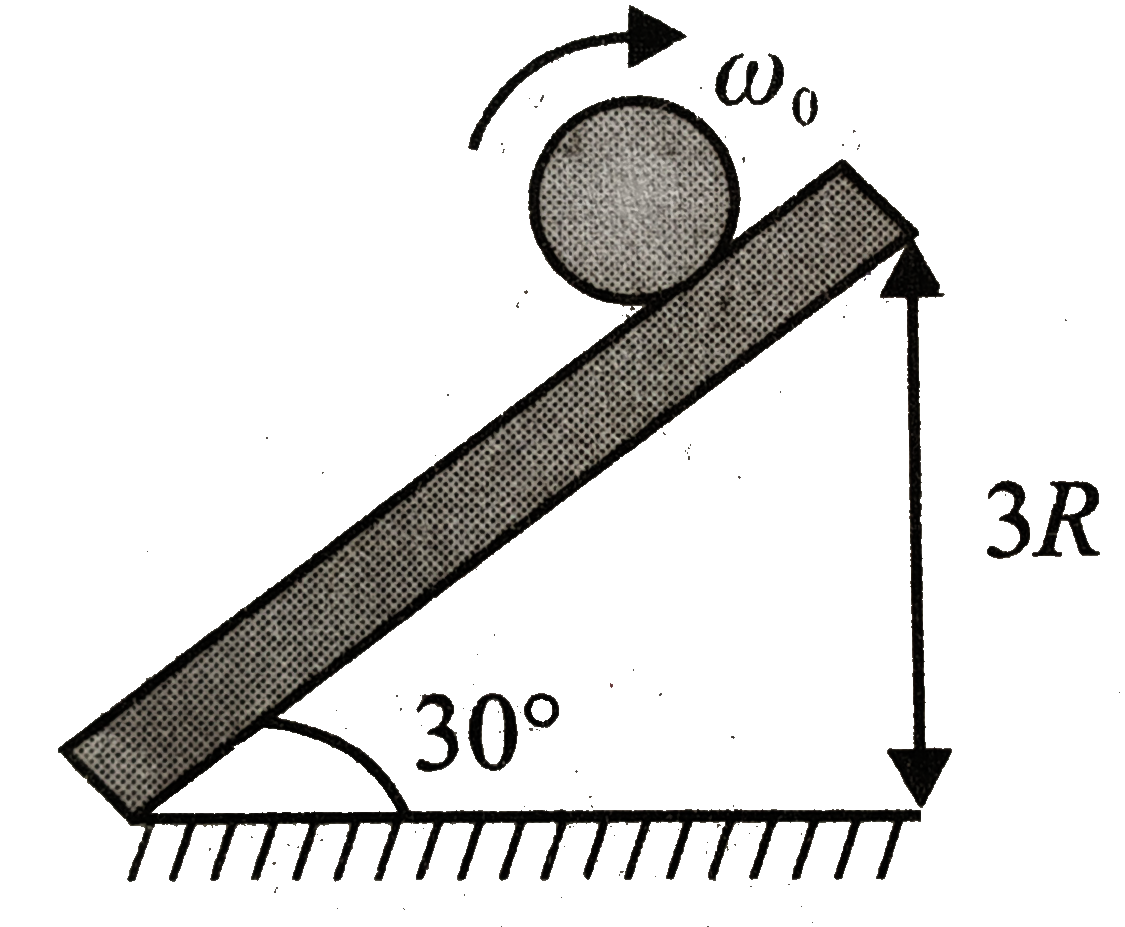
A spinning cylinder with angular velocity ω0 of mass M and radius R is lowered on a rough inclined plane of angle 30∘ with the horizontal and μ=1/√3. The cylinder is released at a height of 3R from horizontal. Find the total time taken by the cylinder to reach the bottom of the incline.
The correct Answer is:√Rg
We will check whether the cylinder slips down the incline or not
As mgsin30∘=μmgcos30∘ initially the cylinder slips at its place till the angular velocity becomes zero.

Στ=(μmgcosθ)R=mR22α
α=2μcosθRg
0=ω0−α1 or t1=ω0α
Next the sphere will come down with initial angular and linear velocity both zero.
fR=mR22α⇒f=mRα2
and mgsinθ−f=ma
If pure rolling takes place a=Rα.
⇒2f=ma
mgsiθ=3f
f=13mgsinθ⇒f=16mg
As fmax=μmcosθ=1√3mg×√32=mg2
and fmax<f so pure rolling is possible.
a=2fm=2(mg/6)mm=g3
Let t2 be the time taken to reach the foot of the incline.
3Rsin30∘=12g3t22 or t2=6√R6
Hence total time t=t1+t2(ω0Rg+6√Rg)
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct
142 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.4
13 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A uniform ball of radius r rolls without slipping down from the top of a sphere of radius R Find the angular velocity of the ball at the moment it breaks off the sphere. The initial velocity of the ball is negligible.
View SolutionA ring rolls without slipping on the ground. Its centre C moves with a constant speed u.P is any point on the ring. The speed of P with respect to the ground is v.
View SolutionA sphere rolling on a horizontal rough surface Collides elastically with a smooth vertical wall, as shown in Fig. State which of the following statements is true or false.
 a. After collision, the velocity of the centre of mass gets reversed.
a. After collision, the velocity of the centre of mass gets reversed.
b. Angular momentum of the sphere about the point of contact with the wall is conserved.
c. Angular momentum of the sphere about a stationary point on the horizontal surface is conserved.
d. Just after collision the point of contact with the horizontal surface is moving towards the wall.
e. After collision the friction force acts on the sphere such that it decreases the linear speed and increases the angular speed.
f. Finally, when the sphere starts rolling, it is moving away from the wall.
View SolutionA solid cylinder with r=0.1m and mass M=2kg is placed such that it is in contact with the vertical and a horizontal surface as shown in Fig. The coefficient of friction is μ=(1/3) for both the surfaces. Find the distance (in CM) from the centre of the cylinder at .which a force F=40N should be applied vertically so that the cylinder just starts rotating in anticlockwise direction.

View SolutionThe average power transmitted across a cross section by two sound waves moving in the same direction are equal. The wavelength of two sound waves are in the ratio of 1:2, then find the ratio of their pressure amplitudes.
View SolutionA uniform cylinder of mass M and radius R is released from rest on a rough inclined surface of inclination theta with the horizontal as shown in figure. As the cylinder rolls down the inclined surface, the maximum elongation it the spring stiffness k is
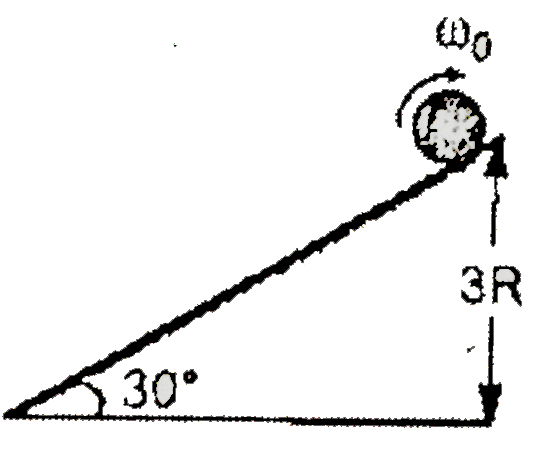
View SolutionA spinning cylinder with angular velocity omega_(0) of mass M and radius R is lowered on a rough inclined plane of angle 30^@ with the horizontal and mu = 1//sqrt(3) . The cylinder is released at a height of 3R from horizontal. Find the total time taken by the cylinder to reach the bottom of the incline.
View SolutionA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
View SolutionA cylinder of mass m radius R is spined to a clockwise angular velocity ωo and then gently placed on an inclined plane for which coefficient of friction μ=tanθ,θ is the angle of inclined plane with the horizontal. The centre of mass of cylinder will remain stationary for time

View SolutionA spinning cylinder of mass m and radius R is lowered on a rough inclined plane of angle 30∘ with the horizontal and μ=1√3. The cylinder is released at a height of 3R from horizontal. Find the total time taken by the cylinder to reach the bottom of the incline.
View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h. The angular velocity of the cylinder when it reaches the bottom of the plane will be :
View SolutionA cylinder is released from the top of an incline making angle theta=45^(@) with the horizontal. The length of the incline is 2.82m and mass of cylinder is 1kg . The coefficient of friciton is 0.2 between the cylinder and the incline. When the cylinder reaches the bottom of the incline, its total kinetic energy is (g=10m//s^(2))
View SolutionA solid cylinder rolls down from an inclined plane of height h. What is the velocity of the cylinder when it reaches at the bottom of the plane ?
View SolutionA solid cylinder rolls up an inclined plane of angle of inclination 30^(@) . At the bottom of the inclined plane the centre of mass of the cylinder has a speed of 5 "m.s"^(-1) . Time taken for the cylinder to return to the bottom is
View SolutionA cylinder is rotating with angular velocity omega_(0) and is gently put on a rough horizontal floor. Assume mass of the cylinder is m and radius R. Calculate the velocity of cylinder when it starts pure rolling on the surface.
View SolutionA uniform cylinder of mass M and radius R is released from rest on a rough inclined surface of inclination theta with the horizontal as shown in figure. As the cylinder rolls down the inclined surface, the maximum elongation it the spring stiffness k is
View Solution

