A streched string is forced to transmit transverse waves by means of an oscillator coupled to one end. The string has a diameter of 4mm. The amplititude of the oscillation is 10−4 m and the frequency is 10Hz. Tension in the string is 100 N and mass density of wire is 4.2×103kg/m3. Find
(a) the equation of the waves along the string
(b) the energy per unit volume of the wave
(c) the average energy flow per unit time across any section of the string and
(d) power required to drive the oscillator.
The correct Answer is:A, B, C, D
(a) Speed of transverse wave on the string is
v=√TρS (asμ=ρS)
Substituting the values,we have
v=
⎷100(4.2×103)(π4)(4.0×10−3)2=43.53m/s
ω=2πf=20π=62.83rad/s
k=ωv=1.44m−1
:. Equation of the waves along the string, y(x,t)=Asin(kx−ωt)
=(10−4m)sin[(1.44m−1)x−(62.83rade/s)t]
(b) Energy per unit volume of the string,u=energy density=12ρω2A2
Subsitutituting the values, we have
=u=(12)(4.2×103)(62.83)2(10−4)2
=8.29×10−2J/m3
(c) Average energy flow per unit time, P=power=(12ρω2A2)(Sv)=(u)(Sv)
Susbstituting the values, we have P=(8.29×10−2)(π4)(4×10−3)2(43.53)
4.53×10−5J/s
(d) Therefore, power required to drive the oscillator is 4.53×10−5W.
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Example Type 1
1 Video
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Example Type 2
1 Video
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
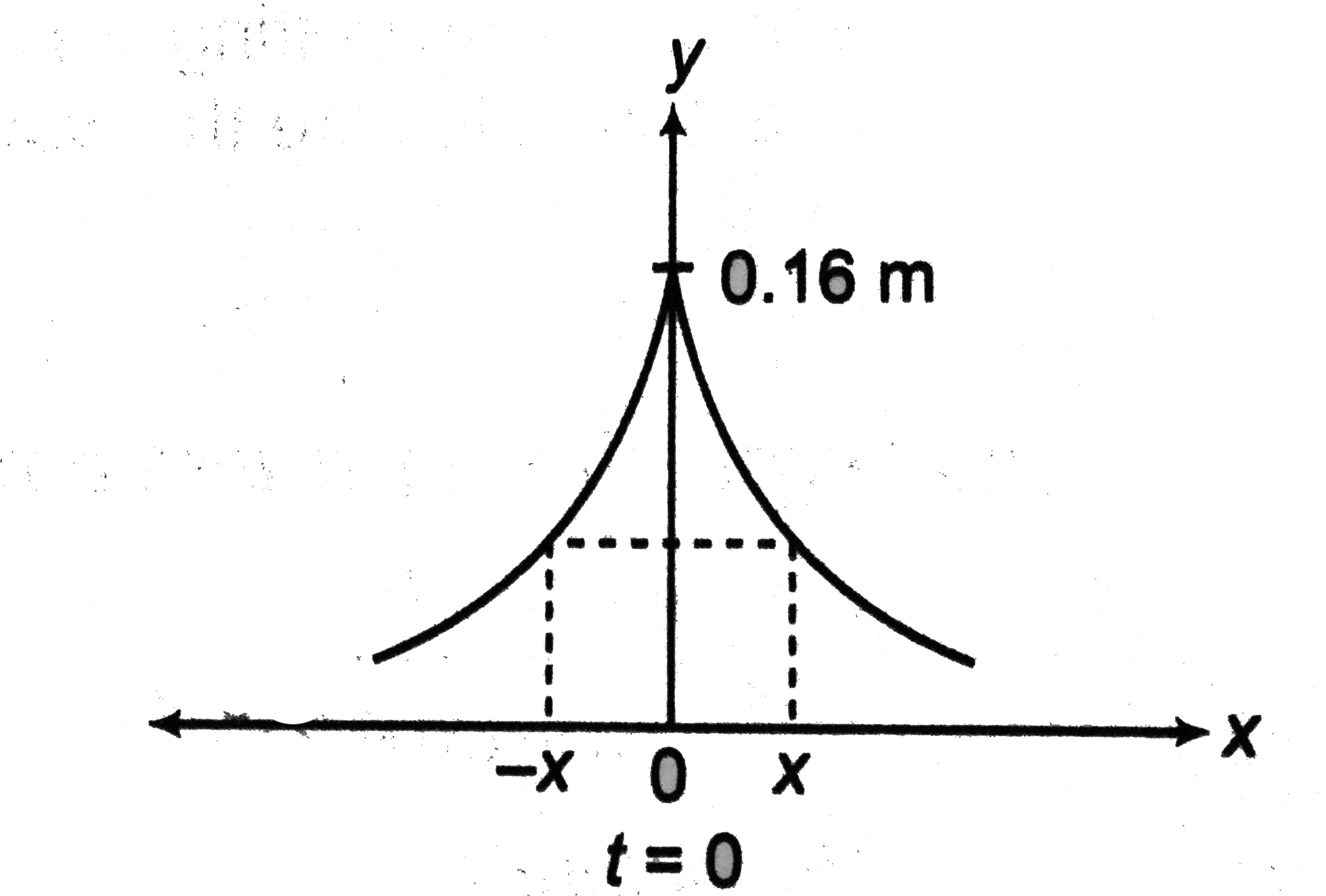
y(x,t)=0.8[(4x+5t)2+5] represents a moving pulse where x and y are in metre and t in second. Then,choose the correct alternative(s):
(a) pules is moving in positive x- direction
(b) in 2s it will travel a distance of 2.5m
(c) its maximum displacement is 0.16m
(d) it is a sysmmetric pulse
View SolutionAt time t=0,y(x) equation of a wave pulse is
y=102+(x−4)2
and at t=2s, y(x) equation of the same wave pulse is
y=102+(x+4)2
Here, y is in mm and x in metres. Find the wave velocity.
View SolutionIf the magnitude of sum of two vectors is equal to the magnitude of difference of the two vector, the angle between these Vector is
View SolutionThe figure shows the variation of potential energy of a particle as a function pf x, the x-coordination of the region. It has been assumed that potential energy depends only on x. For all other values x,U is zero. i.e. forx<−10 and x>15,U=0.
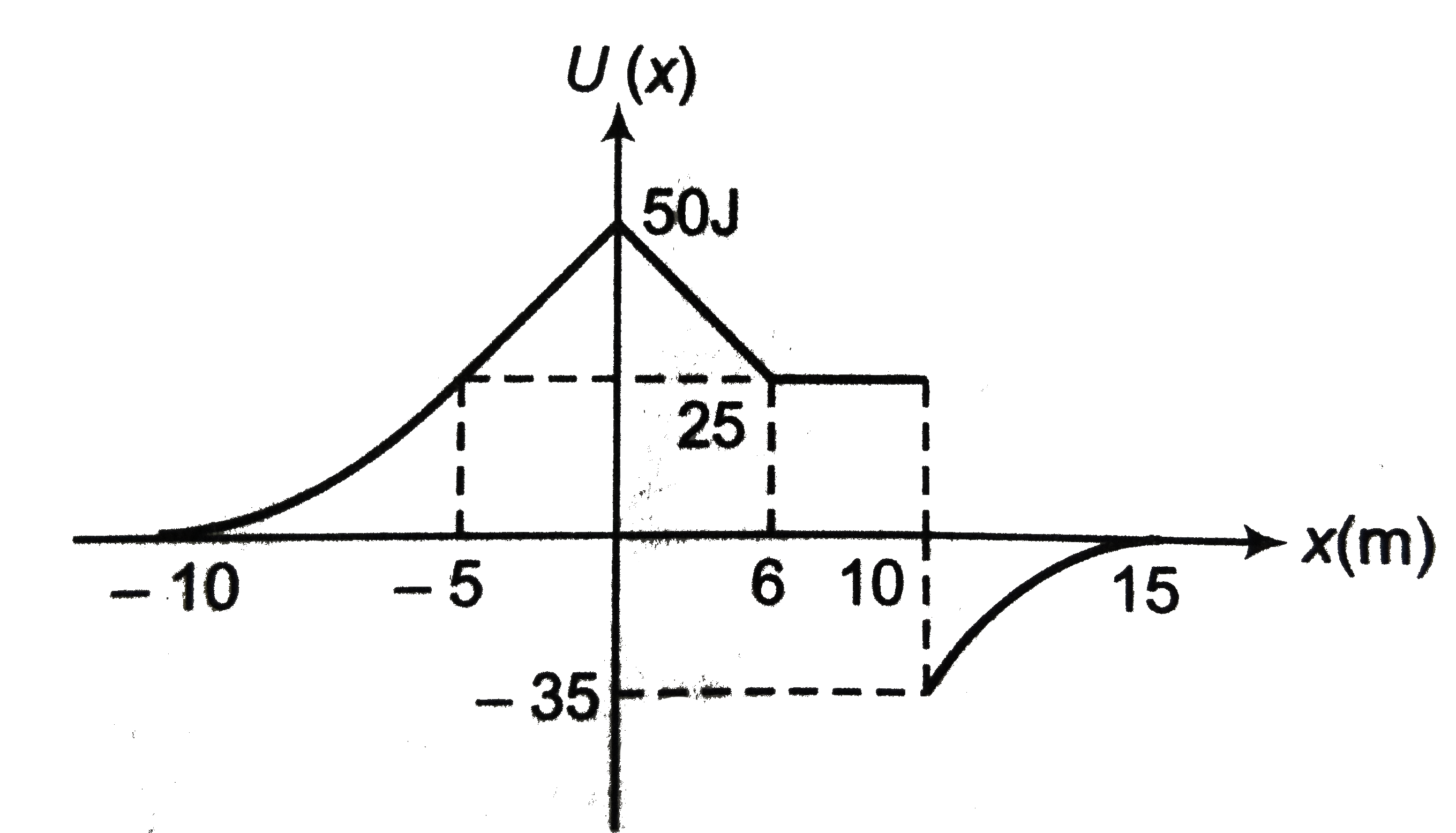
If total mechanical energy of the particle is 25J, then it can found in the region
View SolutionA streched string is forced to transmit transverse waves by means of an oscillator coupled to one end. The string has a diameter of 4mm. The amplititude of the oscillation is 10−4 m and the frequency is 10Hz. Tension in the string is 100 N and mass density of wire is 4.2×103kg/m3. Find
(a) the equation of the waves along the string
(b) the energy per unit volume of the wave
(c) the average energy flow per unit time across any section of the string and
(d) power required to drive the oscillator.
View SolutionA string of 7 m length has a mass of 0.035 kg. If tension in the string is 60.5 N. Then speed of a wave on the string is
View SolutionA string of 7 m lengt has a mass of 0.035 kg. If tension in the string is 60.5 N, then speed of a wave on the string is
View SolutionA string is stretched by a force of 40 newton. The mass of 10 m length of this string is 0.01 kg. the speed of transverse waves in this string will be
View SolutionA transverse harmonic wave is propagating along a taut string. Tension in the string is 50 N and its linear mass density is 0.02 kg m^( –1) The string is driven by a 80 Hz oscillator tied to one end oscillating with an amplitude of 1mm. The other end of the string is terminated so that all the wave energy is absorbed and there is no reflection (a) Calculate the power of the oscillator. (b) The tension in the string is quadrupled. What is new amplitude of the wave if the power of the oscillator remains same? (c) Calculate the average energy of the wave on a 1.0 m long segment of the string.
View SolutionA string of 7 m length has a mass of 0.035 kg. If tension in the string is 60.5 N, then speed of a wave on the string is :
View SolutionA 5.5 m length of string has a mass of 0.035 kg. If the tension in the string is 77 N, the speed of a wave on the string is :
View SolutionThe mass of a string is 5.0 xx 10^(-3) kg, and it is stretched so that the tension in it is 180 N. A transverse wave traveling on this string has a frequency of 260 Hz and a wavelength: of 0.60 m. What is the length of the string?
View SolutionIn a stretched string, transverse waves are produced with the help of a oscillator. The chord has a diameter of 4 mm. Oscillation amplitude 10^(-4) M and frequency is 10 Hz. Strain in lanyard 100 Newton and mass density of lanyard 4.2xx10^3 Kg "मी"^(-3) is. Find out (a) Equation of wavelength along the string. (b) Volume energy per unit of wave.
View SolutionA 5.5 m long string has a mass of 0.035 kg. If the tension in the string is 77 N, the speed of a wave on the string is
View SolutionThe speed of a wave along a stretched string depends only on the tension and linear mass density of the string and does not dependent on the frequency of the wave. Give the equation of speed of transverse wave along a stretched string.
View SolutionThe speed of a wave along a stretched string depends only on the tension and linear mass density of the string and does not dependent on the frequency of the wave.
A steel wire 0.72 long has a mass of 5×10−3kg,if the wire is under a tension 60N,what is the speed of transverse wave on the wire?
View Solution

