A string of length L, fixed at its both ends is vibrating in its 1st overtone mode. Consider two elements of the string of the same small length at positions l1=0.2Landl2=0.45L from one end.
If K1andK2 are their respective maximum kinetic energies,then
k1=K2
K1>K2
K1<K2
it is not possible to decide the relation
The correct Answer is:A
Step by step video solution for A string of length L, fixed at its both ends is vibrating in its 1^(st) overtone mode. Consider two elements of the string of the same small length at positions l_(1)=0.2L"and"l_(2)=0.45L from one end. If K_(1)"and" K_(2) are their respective maximum kinetic energies,then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Subjective Type
2 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Video
Similar Questions
A standing wave pattern of maximum amplitude 2 mm is obtained in a string whose shape at t = 0 is represented in the graph.
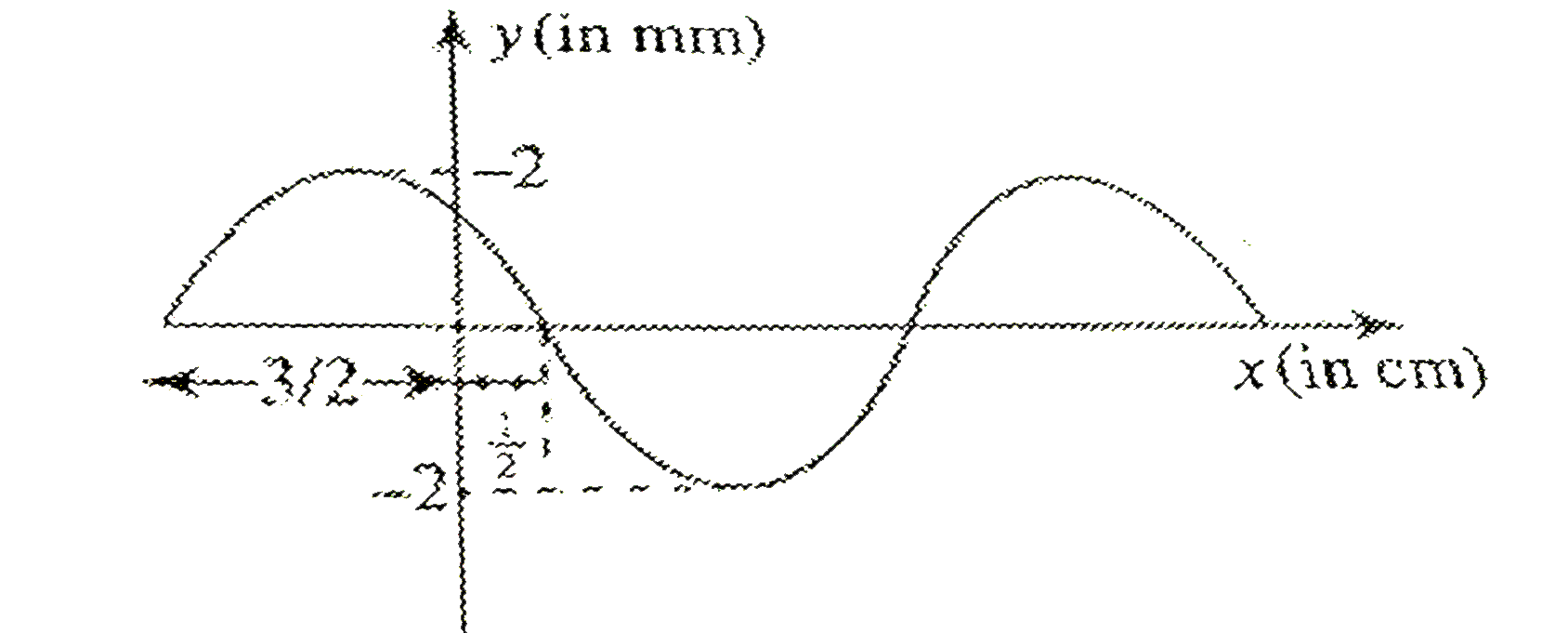
If the speed of the travelling wave in the string is 5 cm/s, then find the component waves.
View SolutionThe average power transmitted across a cross section by two sound waves moving in the same direction are equal. The wavelength of two sound waves are in the ratio of 1:2, then find the ratio of their pressure amplitudes.
View SolutionDuring the adiabatic expansion of 2 moles of a gas, the internal energy of the gas is found to decrease by 2 joules , the work done during the process on the gas will be equal to
View SolutionA spring of length 'l' has spring constant 'k' is cut into two parts of length l_(1) and l_(2) . If their respective spring constahnt are K_(1) and k_(2) , then (K_(1))/(K_(2)) is:
View SolutionA string of length 'l' is fixed at both ends. It is vibrating in its 3rd overtone with maximum ampltiude 'a'. The amplitude at a distance l3 from one end is =√pa2. Find p.
View SolutionA string of length L fixed at its at its both ends is vibrating in its 1^(st) overtone mode. Consider two elements of the string of same small length at position l_1=0.2L and l_2=0.45L from one end. If K_1 and K_2 are their respective maximum kinetic energies then
View SolutionA string of length L, fixed at its both ends is vibrating in its 1st overtone mode. Consider two elements of the string of the same small length at positions l1=0.2Landl2=0.45L from one end.
If K1andK2 are their respective maximum kinetic energies,then
View SolutionA string of length L, fixed at its both ends is vibrating in its 1^(st) overtone mode. Consider two elements of the string of the same small length at positions l_(1)=0.2L"and"l_(2)=0.45L from one end. Follow situation of part (a) If K_(1) "and" K_(2) are respective force constants of their simple hrmonic motions, then
View SolutionA string of mass 'm' and length l, fixed at both ends is vibrating in its fundamental mode. The maximum amplitude is 'a' and the tension in the string is 'T'. If the energy of vibrations of the string is π2a2TηL. Find η
View SolutionA string of length 'l' is fixed at both ends. It is vibrating in its 3rd overtone with maximum ampltiude 'a'. The amplitude at a distance l3 from one end is =√pa2. Find p.
View SolutionA string of mass 'm' and length l, fixed at both ends is vibrating in its fundamental mode. The maximum amplitude is 'a' and the tension in the string is 'T'. If the energy of vibrations of the string is π2a2TηL. Find η
View Solutionसमान अनुप्रस्थ काट की दो छड़े एक-दूसरे से सटाकर रखी गयी है जिनकी लम्बाइयाँ क्रमश: l1 तथा l2 तथा ऊष्मा चालकताएँ K1 व K2 है | सिद्ध कीजिये कि स्थायी अवस्था में छड़ो के सिरों के तापान्तर का अनुपात K2l1:K1l2 होगा |
View SolutionA string of length L fixed at both ends vibrates in its first overtone. Then the wavelength will be
View SolutionA wire of length L is hanging from a fixed support. The length changes to L1andL2 when masses M1andM2 are suspended respectively from its free end. Then L is equal to
View SolutionA string of mass per unit length "0.2 kg m"^(-1) and length 0.6 m is fixed at both ends such that it has a tension of 80 N. If the string is vibrating in its second overtone mode, then the frequency of the string is
View SolutionA spring of length 'l' has spring constant 'k' is cut into two parts of length l_(1) and l_(2) . If their respective spring constahnt are K_(1) and k_(2) , then (K_(1))/(K_(2)) is:
View Solution

