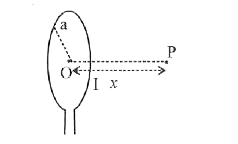
A student records the following data for the magnitudes (B) of the magnetic field at axial points at different distances x from the centre of a circular coil of radius 'a' carrying a current I. Verify (for any two) that these observations are in good agreement with the expected theoretical variation of B with x.
 Solution in Tamil
Solution in Tamil
Magnetic field (B) is givenB=μ04π=2Mx2
Similar Questions
Using Biot - Savart's law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.
View SolutionUsing Biot-Savart’s law, derive an expression for magnetic field at any point on axial line of a current carrying circular loop. Hence, find magnitude of magnetic field intensity at the centre of circular coil.
View SolutionA circular coil of radius 2R is carrying current 'i' . The ratio of magnetic fields at the centre of the coil and at a point at a distance 6R from the centre of the coil on the axis of the coil is
View SolutionA circular coil of radius 2R is carrying current 'i'. The ratio of magnetic fields at the centre of the coil and at a point at a distance 6R from the centre of the coil on the axis of the coil is
View SolutionA circular coil of radius R carries a current i. The magnetic field at its centre is B. The distance from the centre on the axis of the coil where the magnetic field will be B/8 is
View SolutionA circular coil of radius R carries a current I. The magnetic field at its centre is B. At what distance from the centre, on the axis of the coil the magnetic field will be B8 ?
View SolutionA student records the following data for the magnitudes (B) of the magnetic field at axial points at different distances x from the centre of a circular coil of radius a carrying a current I. Verify (for any two) that these observations are in good agreement with the expected the oretical variation of B with x.
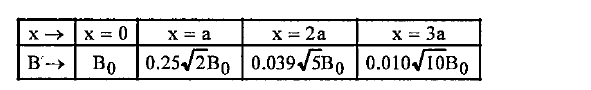
View SolutionA circular coil of radius 2R is carrying current I. The ratio of magnetic fields at the centre of coil and at a point at a distance 6R from centre of coil on axis of coil is
View Solution
