A thin circular wire of radius R rotatites about its vertical diameter with an angular frequency ω . Show that a small bead on the wire remain at its lowermost point for ω≤√g/R . What is angle made by the radius vector joining the centre to the bead with the vertical downward direction for ω=√2g/R ? Neglect friction.
Step by step video & image solution for A thin circular wire of radius R rotatites about its vertical diameter with an angular frequency omega . Show that a small bead on the wire remain at its lowermost point for omegalesqrt(g//R) . What is angle made by the radius vector joining the centre to the bead with the vertical downward direction for omega=sqrt(2g//R) ? Neglect friction. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem
24 Videos
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice
90 Videos
- PROPERTIES OF SOLIDSBOOK - SL ARORACHAPTER - PROPERTIES OF SOLIDSEXERCISE - All Questions
97 Videos
- System of particles & rotational MotionBOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE
353 Videos
Similar Questions
An isolated particle of mass m is moving in a horizontal plane (x-y), along the x-axis at a certain height above the ground. It suddenly explodes into two fragments of masses m/4 and 3m/4. At instant later, the smaller fragment is at y=+5cm. What is the position of larger fragment at this instant ?
View SolutionThe distance between the carbon atom and the oxygen atom in a carbon monoxide molecule is 1.1Å. Given, mass of carbon atom is 12 a.m.u. and mass of oxygen atom is 16 a.m.u., calculate the position of the centre of mass of the carbon monoxide molecule
View SolutionA wire increases by 10−3 of its length when a stress of 1×108Nm−2 is applied to it. What is the Young's modulus of the material of the wire?
View SolutionTwo bodies of masses 1 kg and 2 kg are located at (1,2) and (-1,3), respectively. Calculate the coordinates of center of mass.
View SolutionA thin circular wire of radius R rotatites about its vertical diameter with an angular frequency ω . Show that a small bead on the wire remain at its lowermost point for ω≤√g/R . What is angle made by the radius vector joining the centre to the bead with the vertical downward direction for ω=√2g/R ? Neglect friction.
View SolutionA thin ring of radius R is made of a material of density rho and Young's modulus Y. If the ring is rotated about its centre in its own plane with angular velocity omega , find the small increases in its radius.
View SolutionA smooth wire is bent into a vertical circle of radius a. A bead P can slide smoothly on the wire. The circle is rotated about vertical diameter AB as axis with a speed omega as shown in figure. The bead P is at rest w.r.t. the circular ring in the position shown. then ω2 is equal to:

View SolutionA small bead of mass 'm' is threaded on a frictionless circulat wire of radius 'a' . The circule wire frame is rotated about its vertical diameter as shown. (assume acceleration due to grasvity is g) The angular speed required if the bead is to be made to move in a horizontal circle of radius (a sqrt(3))/(2) is :
View SolutionA circular wire frame of radius R is rotating about its fixed vertical diameter. A bead on the wire remains at rest relative to the wire at a position in which the radius makes an angle θ with the vertical (see figure). There is no friction between the bead and the wire frame. Prove that the bead will perform SHM (in the reference frame of the wire) if it is displaced a little from its equilibrium position. Calculate the time period of oscillation.
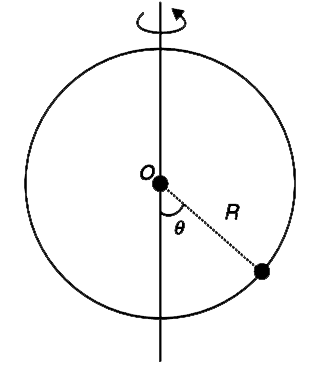
View SolutionR त्रिज्या का पतला वृत्तीय तार अपने ऊर्ध्वाधर व्यास के परितः कोणीय आवृत्ति ω से घूर्णन कर रहा है । यह दर्शाइए कि इस तार में डली कोई मणिका ω≤√g/R के लिए अपने निम्नतम बिंदु पर रहती है | ω=√2g/R के लिए, केंद्र से मणिका को जोड़ने वाला त्रिज्य सदिश ऊर्ध्वाधर अधोमुखी दिशा से कितना कोण बनाता है ।
(घर्षण को उपेक्षणीय मानिए ।)
View SolutionA thin circular loop of radius R rotates about its vertical diameter with an angular frequency omega . Show that a small bead on the wire loop remains at its lowermost point for omegalesqrt(g//R) . What is the angle made by the radius vector joining the centre to bead with the vertical downward direction for omega=sqrt(2g//R) ? Neglect friction .
View SolutionA circular loop has a small bead which can slide on it without friction. The radius of the loop is r. Keeping the loop vertically it is rotated about a vertical diameter at a constant angular speed omega . What is the value of angle theta , when the bead is in dynamic equilibrium ?
View SolutionA thin circular loop of radius R rotates about its vertical diameter with an angular frequency ω . Show that a small bead on the wire loop remains at its lowermost point for ω<√g/R What is the angle made by the radius vector joining the centre to the bead with the vertical downward direction for ω=√2g/R ? neglect friction.
View SolutionA thin circular loop of radius R rotates about its vertical diameter with an angular frequency omega . Show that a small bead on the wire loop remains at its lowermost point for omega lt sqrt( g// R) What is the angle made by the radius vector joining the centre to the bead with the vertical downward direction for omega = sqrt(2g// R) ? neglect friction.
View SolutionA thin circular wire of radius R rotates about its vertical diameter with an angular frequency omega . Show that a small bead on the wire remain at its lowermost point for omegalesqrt(g//R) . What is angle made by the radius vector joining the center to the bead with the vertical downward direction for omega=sqrt(2g//R) ? Neglect friction.
View SolutionA thin ring of radius R is made of material of density P and young.s modulus Y. If the ring is rotated about its centre and in its own plane with angular velocity ω find the small increase in its radius.
View Solution

