A thin spherical shell of radius R lying on a rough horizontal surface is hit sharply and horizontally by a cue. Where should it be hit so that the shell does not slip on the surface?
To solve the problem of where to hit a thin spherical shell so that it does not slip on a rough horizontal surface, we can follow these steps:
1. Understanding the Problem: We have a thin spherical shell of radius R resting on a rough horizontal surface. When it is struck by a cue, we need to determine the height H at which it should be hit to ensure that it rolls without slipping.
2. Identify the Forces: When the shell is hit, it experiences a force due to the cue and a frictional force from the surface. The frictional force will help in rolling the shell without slipping.
3. Pure Rolling Condition: For the shell to roll without slipping, the condition Vc=Rω must hold, where Vc is the velocity of the center of mass and ω is the angular velocity.
4. Applying Conservation of Angular Momentum: We can apply the principle of conservation of angular momentum about the point of contact (let's call it point A). The equation can be set up as:
−μcFfriction⋅H−I⋅α=0
where μc is the coefficient of friction, Ffriction is the frictional force, I is the moment of inertia of the shell, and α is the angular acceleration.
5. Moment of Inertia: The moment of inertia I of a thin spherical shell about its center is given by:
I=23mR2
6. Relating Linear and Angular Acceleration: The linear acceleration a of the center of mass is related to the angular acceleration α by the equation:
a=Rα
7. Setting Up the Equations: Substitute the expressions for I and a into the angular momentum equation. The frictional force can be expressed as Ffriction=μcN, where N is the normal force (equal to mg for a horizontal surface).
8. Solving for Height H: After substituting and simplifying, we find that:
H=23R
This means that the cue should strike the shell at a height of 23R from the bottom of the shell.
Final Answer:
The cue should hit the shell at a height of 23R from the bottom to ensure that it rolls without slipping.
---
−μcFfriction⋅H−I⋅α=0
where μc is the coefficient of friction, Ffriction is the frictional force, I is the moment of inertia of the shell, and α is the angular acceleration.
I=23mR2
a=Rα
H=23R
This means that the cue should strike the shell at a height of 23R from the bottom of the shell.
The cue should hit the shell at a height of 23R from the bottom to ensure that it rolls without slipping.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Subjective
Explore 19 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Single Correct
Explore 142 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.3
Explore 21 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICS ENGLISHChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A uniform sphere of radius R is palced on a rough horizontal surface and given a linear velocity v0 and an angular velocity ω0 as shown . If the angular velocity and the linear velocity both become zero simultaneously, then
View SolutionA solid sphere of mass M and radius R is placed on a rough horizontal surface. It is stuck by a horizontal cue stick at a height h above the surface. The value of h so that the sphere performs pure rolling motion immediately after it has been stuck is

View Solution
Knowledge Check
Consider a thin spherical shell of radius R consisting of uniform surface charge density σ. The electric field at a point of distance x from its centre and outside the shell is
Ainversely proportional to σBdirectly proportional to x2Cdirectlr proportional to RDinversely proportional to x2
When a body is rolling without slipping on a rough horizontal surface, the work done by friction is :
View SolutionA disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.

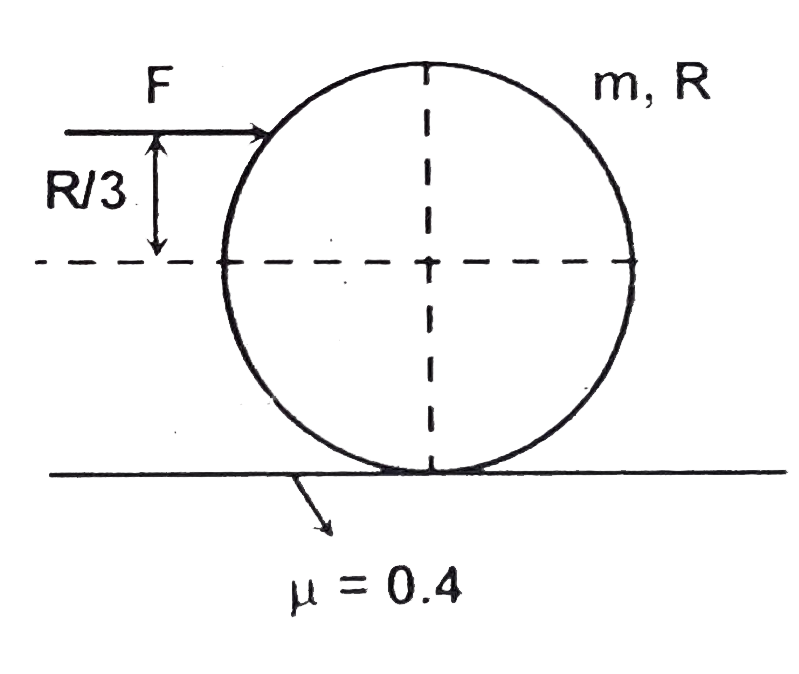
View SolutionA thin uniform spherical shell of mass m=2kg and radius R=10cm is placed on a rough horizontal surface with a coefficient of friction μ=0.4. A horizontal force 'F' is applied to the spherical shell at a height R/3 ablove the centre as shown. The maximum magnitude of the applied force 'F' for which the spherical shell will be rolling without slipping is (taking g=10m/a2 )
View SolutionUniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force is applied at the top point P of the cylinder so that it start pure rolling .In the above question, the frictional force on the cylinder is
View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
View Solution
A solid sphere of mass ma nd radis R is placed on a rough horizontal surface A horizontal force F is applied to sphere at a height h, (0≤h≤R) from centre. If sphere rolls slipping then,
View SolutionA solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to

View Solution
