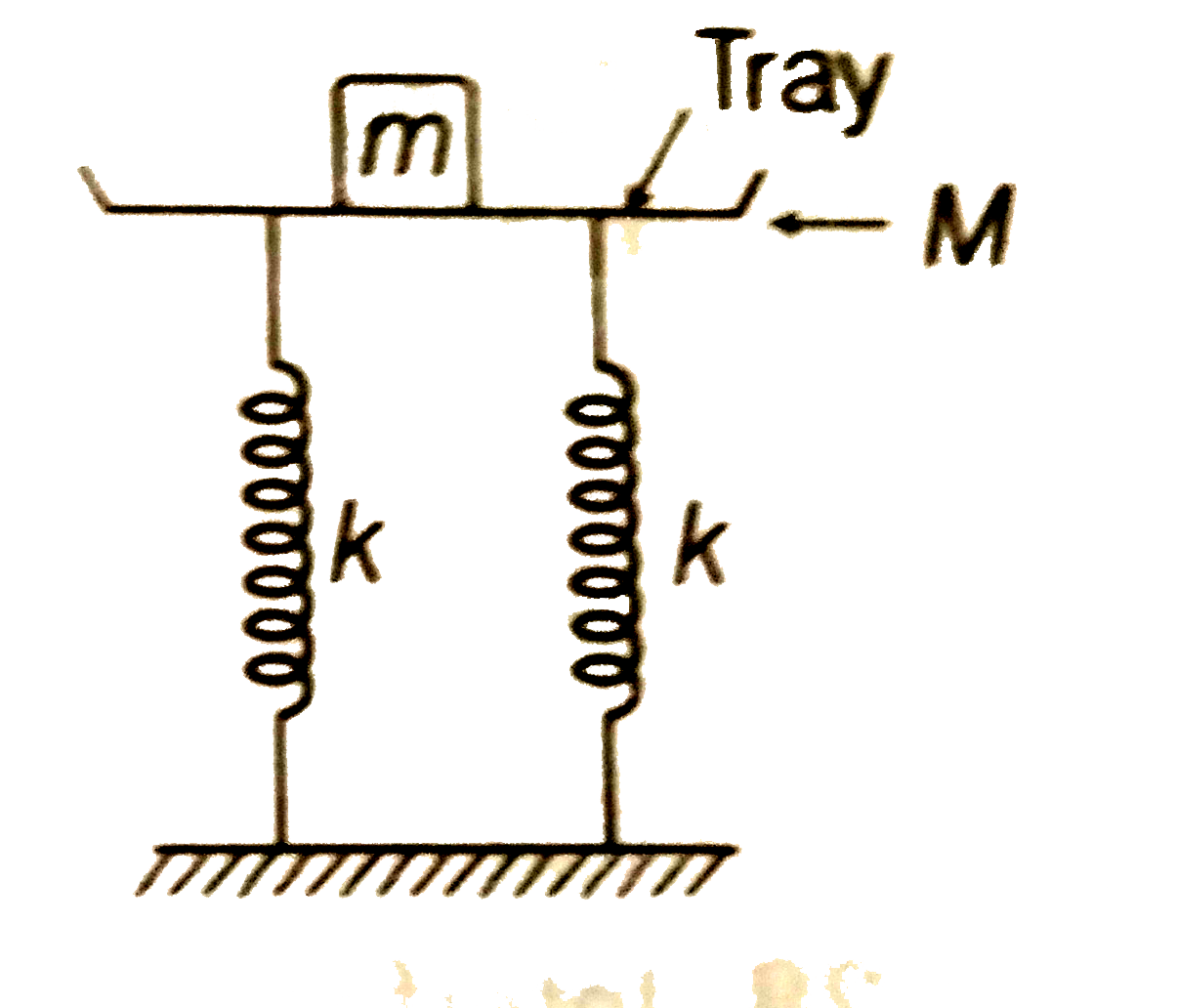
A tray of mass M=10kg is supported on two identical springs, each of spring constant k, as shown in figure, when the tray is depressed a little and released, it executes simple harmonic motion of period 1.5 s. when a blockof mass m is placed on the tray, the speed of oscillation becomes 3 s. the value of m is
10 kg
20 kg
30 kg
40 kg
The correct Answer is:C
There are two identical springs which are connected in parallel, ltBrgt ∴ The effective spring consistant of the combination is
k'=k+k=2k
∴ Time period
T=2π√Mk'=2π√M2k . . . (i)
when block of mass m is placed in the tray, the period of oscillation becomes
T'=2π√M+mk'=2π√M+m2k . . . (ii)
Divide (ii) by (i), we get
T'T=√M+mM⇒31.5=√10+m10
On squaring both sides, we get
4=10+m10 or 40=10+m
or m=30 kg.
টপার এই প্রশ্নগুলো সমাধান করেছে
সম্পর্কিত প্রশ্ন
A body of mass 4 kg is accelerated up by a constant force, travels a distance of 5 m in the first second and a distance of 2m in the third second. The force acting on the body is
View SolutionAMPERE'S CIRCUITAL LAW
View SolutionA mass M is suspended from a spring of negligible mass. The spring is pulled a little then released, so that the mass executes simple harmonic motion of time period T . If the mass is increased by m , the time period becomes (5T)/(3) . Find the ratio of m//M .
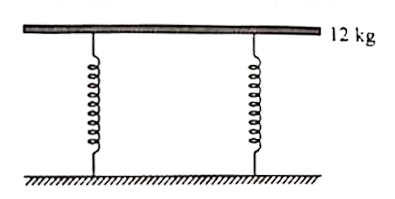
View SolutionA tray of mass 12 kg is supported by two identical springs as shown in figure. When the tray is pressed down slightly and released, it executes SHM with a time period of 1.5s. What is the force constant of each spring?When a block of mass m is placed on the tray , the period of SHM changes to 3.0s. What is the mass of the block ?
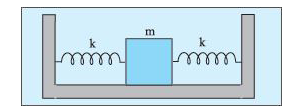
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is
View SolutionA tray of mass 12 kg is supported by tow identical spring as shown in figure. When the tray is pressed down slightly and then relased , it executes SHM with a time peroid of 1.5 s.The spring constant of each spring is .
View SolutionA mass 'M' is suspended from a spring of negligible mass. The spring is pulled a little and then released. It execuutes S.H. oscillations of period T. When mass is increased by 'm', the period becomes (5)/(4) T, the ratio (m)/(M) is :
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in Fig. 14.14. Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillations.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in Fig. 14.14. Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillations.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillation.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in Fig. 14.14. Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillations.
View SolutionA mass M is suspended from a spring of negligible mass. The spring is pulled a little and then released so that the mass executes simple harmonic oscillation with a time period T. If the mass is increased by m, the time period becomes ((5)/(4)T) . The ratio of (m)/(M) is...........
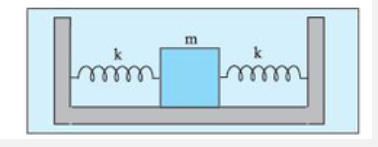
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in Fig. 14.14. Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillations.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in Fig. 14.14. Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillations.
View Solution
A tray of mass M=10kg is supported on two identical springs, each of spring constant k, as shown in figure, when the tray is depressed a little and released, it executes simple harmonic motion of period 1.5 s. when a block of mass m is placed on the tray, the speed of oscillation becomes 3 s. the value of m is
View Solution
