A uniform rod of mass m and length l is kept vertical with the lower end clamped. It is slightly pushed to let it fall down under gravity. Find its angular speed when the rod is passing through its lowest position. Neglect any friction at the clamp. What will be the linear speed of the free end at this instant?
As the rod reaches its lowest position, the centre of mass is lowered by a distance l. its gravitational potential energy is decreased by mg. As no energy is lost against fricrtion, this should be equal to the increase in th kinetic energy. As the rotation occurs about the horizontal axis through the clamped end, the moment of inertia is I=m2/3. Thus,
12Iω2=mg12(ml22)ω2=mg
or ω=√6gl
The linear speed of the free end is v=lω=√6gl

Similar Questions
A uniform rod of mas m and length l is kept vertical with the lower end clamed. It is slightly pushed to let it fall down under gravity. Find its angular speed when the rod is passing through its lowest positon. Neglect any friction at the clamp. What will be the linear speed of the free end at this instant?
View SolutionA rod of mass M and length L is falling vertically with speed v. Suddenly its one end gets stuck in a friciitonless hook. Find the angular velocity of the rod just after its end gets struck.

View Solution
Knowledge Check
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 A2π√lgB2π√2lgC2π√2l3gD2π√l3g
A2π√lgB2π√2lgC2π√2l3gD2π√l3gA thin rod of mass m and length l is suspended from one of its ends. It is set into oscillation about a horizontal axis. Its angular speed is ω while passing through its mean position. How high will its centre of mass rise from its lowest position ?
Aω2l22gBω2l23gCω2l2gDω2l26gA uniform rod of mass and length l is suspended by two strings at its ends shown. When one of the strings is cut, the rod starts falling with an initial angular acceleration.
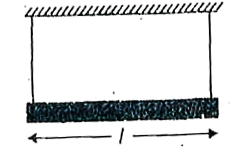 AglBg2lC3g2lD3g4l
AglBg2lC3g2lD3g4l
A uniform rod of mass m and length l is struck at an end by a force F perpendicular to the rod for a short time interval t. Calculate
the angular speed of the rod about the centre of mass,
View SolutionA uniform rod of mass M and length L is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
View SolutionA thin uniform rod of mass m and length l, pivoted freely at its base, is allowed to fall from a vertical position. Calcualte its angular velocity and acceleration when it has turned through 60∘.
View SolutionA thin uniform rod of mass m and length l is free to rotate about its upper end. When it is at rest, it receives an impulse J at its lowest point, normal to its length. Immediately after impact,
View SolutionA thin uniform rod of mass m and length l is free to rotate about its upper end. When it is at rest, it receives an impulse J at its lowest point, normal to its length immediately after impact,
View Solution

