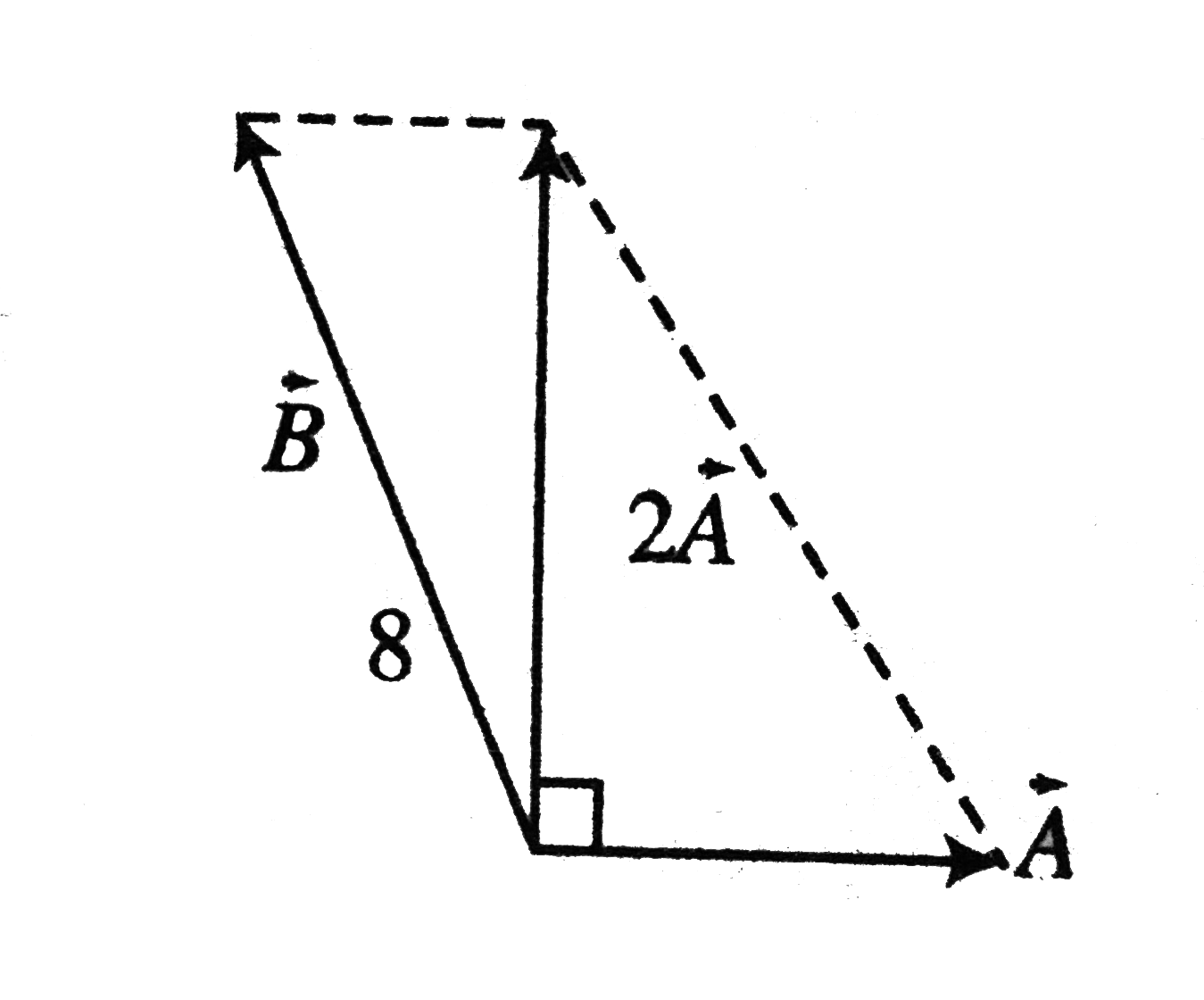
A vector →B which has a magnitude 8.0 is added to a vector →A which lies along the x-axis. The sum of these two vector is a third vector which lies along the y-axis and has a magnitude that is twice the magnitude of →A. Find the magnitude of →A
The correct Answer is:8√5
Angle of resultant is 90∘
∴tananα=sinθa+bcosθ
∴a+bcosθ=0 or cosθ=−ab
Also given (2a)2=(8)2+(a)2+2abcosθ
4a2=64+a2+2ab×(−ab)
5a2=64 or a2=645 or a=8√5
Topper's Solved these Questions
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Single Correct
Explore 51 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise 3.2
Explore 13 Videos
- TRAVELLING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:TRAVELLING WAVESExercise:Integer
Explore 9 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Archives (integer)
Explore 4 Videos
Similar Questions
The sum and diffrence of two perpendicular vector of equal length are
View SolutionWhich of the following statements is/ are correct(Figure)
View Solution→A=2ˆi+4ˆj+4ˆk and →B=4ˆi+2ˆj−4ˆk are two vectors. Find the angles between them.
View SolutionThe speed of a transverse wave going on a wire having a length 50 cm and maas 5.0 g is 80ms−1 The area of cross section of the wire is 1.0mm.2 and its Young modulus is 16×1011Nm−2. Find the extension of the wire over its natural lenth.
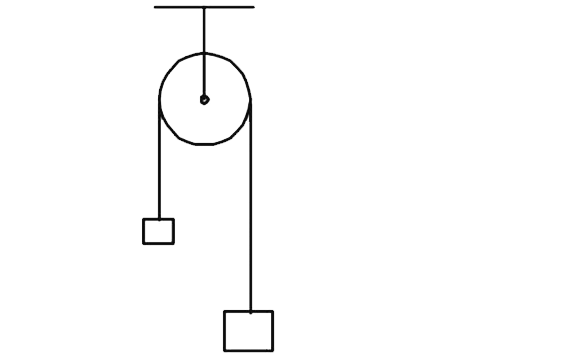
View SolutionA light inextensible string that gas over a smoth fixed polley as shown in the figure connect two blocks of mases it 0.36 kg and 0.72 kg Taking g=10ms−2 , find the work done by the string on the block of mass 0.36 kg doring the first second after the system is released from rest ,
View SolutionA vector →B which has a magnitude 8.0 is added to a vector →A which lies along the x-axis. The sum of these two vector is a third vector which lies along the y-axis and has a magnitude that is twice the magnitude of →A. Find the magnitude of →A
View SolutionA vector vec(A) When added to the vector vec(B)=3hat(i)+4hat(j) yields a resultant vector that is in the positive y-direction and has a magnitude equal to that of vec(B) . Find the magnitude of vec(A) .
View SolutionThe magnitude of the x-component of vector →A is 3 and the magnitude of vector →A is 5. What is the magnitude of the y-component of vector →A ?
View SolutionA vecto →A has magnitude 2 and another vector →B has magnitude 3. They are perpendicular to each other. By vector diagram, find the magnitude of →A+→B and dhow its direcction in the diagram.
View SolutionIf vec(i) and vec(j) are unit vectors along x-axis and y-axis respectively, the magnitude of vector vec(i)+vec(j) will be :-
View SolutionTwo vectors →P and →Q are added, the magnitude of resultant is 15 units. If →Q is reversed and added to →P resultant has a magnitude √113 units. The resultant of →P and a vector perpendicular →P and equal in magnitude to→Q has a magnitude
View Solutionदो वेक्टरो →A और →B का परिणामी वेक्टर →A पर अभिलंबवत है तथा इसका परिमाण वेक्टर →B के परिमाण का आधा है वेक्टरो →A तथा →B के बीच कोण ज्ञात कीजिये ।
View SolutionVector vecA, which is directed along an x axis, is to be added to vector vecB, which has a magnitude of 6.0 m. The sum is a third vector that is directed along the y axis, with a magnitude of vecA Find the magnitude of vecA ?
View SolutionVector vecA, which is directed along an x axis , is to be added to vector vecB, which has a magnitude of 7.0m. The sum is a third vector that is directed along the y axis, with a magnitude that is 3.0 times that of vecA. What is that magnitude of vecA ?
View SolutionA vector barQ which has a magnitude of 8 is added to the vector barP which lies along the X-axis. The resultant of these two vectors is a third vector barR which lies along the Y-axis and has a magnitude twice that of barP . The magnitude of barP is
View SolutionA vector vec(A) when added to the vector vec(B) = 3hat(i) + 4hat(j) yields a resultant vector that is an in the positive y-direction and has magnitude equal to that of vec(B) find the magnitude of vec(A)
View Solution
