A wave is propagating on a long stretched string along its length taken as the positive x-axis. The wave equation is given as
y=y0e−(tT−xλ)2
where y0=4mm,T=1.0sandλ=4cm.(a) find the velocity of wave. (b) find the function f(t) giving the displacement of particle at x=0. (c) find the function g(x) giving the shape of the string at t=0.(d) plot the shape g(x) of the string at t=0 (e) Plot of the shape of the string at t=5s.
(a). The wave equation is
y=Ae−(tT−xλ)2
This may be expressed as
y=Ae−1λ2(x−λT1)2
This is the form f(x−vt)
Therefore,the velocity of wave v=λ/T=8.0/1.0=8cm/s
(b). substituting t=0 in given Eq. (i),we get
f(t)=Ae−(t/T)2
(c ) substituting t=0 in given Eq.(i), we get
g(x)=aE(−(X/LAMBDA)2)
(d). At t=0, the displacement is maximum at the originwhile at t=5s, the displacement is maximum at distance x=vt=8×5=40cm
The function g(x) at t=0 and 5s are plotted in s−5.2 (a) and (b)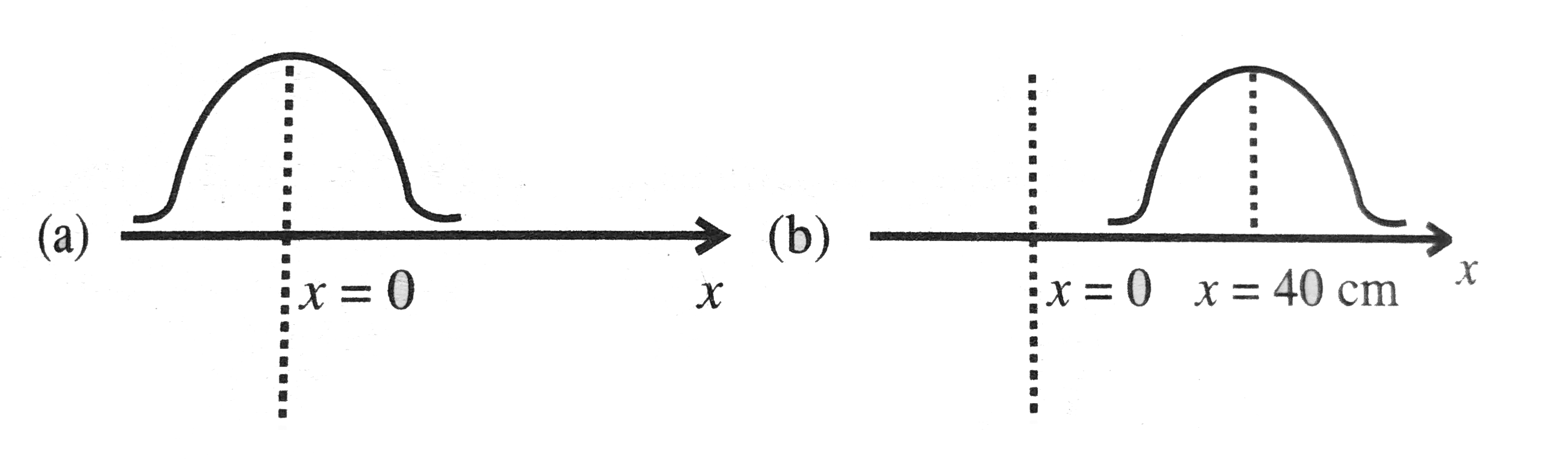
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Subjective
16 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct
62 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.1
9 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A 100Hz sinusoidal wave is travelling in the posotive x-direction along a string with a linear mass density of 3.5×10−3kg/m and a tension of 35N. At time t=0, the point x=0 , has maximum displacement in the positive y-direction. Next when this point has zero displacement, the slope of the string is π/20. Which of the following expression represent (s) the displacement of string as a function of x(in metre) and t (in second)
View SolutionThe speed of a wave in a medium is 960ms−1. If 3600 waves are passing through a point in the medium in one minute then calculate the wavelength.
View SolutionTransverse waves are possible in solids but not in fluids wahy?
View SolutionConsider two hot bodies B1 and B2 which have temperature 100∘C and 80∘C respectively at t = 0. The temperature of surroundings is 40∘ C. The ratio of the respective rates of cooling R1 and R2 of these two bodies att=0 will be
View SolutionWhich of the following statements is/ are correct(Figure)
View SolutionA wave is propgting of a long stretched string along its length taken as the positive x-axis. The wave equation is given as
y=y0e−(tT−xλ)^2
where y0=4mm,T=1.0sandλ=4cm. d. Find the velocity of the particle t x=0. c. Find the function g(x) giving the shape of the string t t=0. d. Plot the shape g(x) of the string at t=0. e. Plot of the shape of the string at t=5s.
View SolutionThe displacement of the particle at x = 0 of a stretched string carrying a wave in the positive x-direction is given by f(t)sin(tT). The wave speed is v. Write the wave equation.
View SolutionA wave propagates on a string in the positive x-direction at a velocity u. The shape of the string at t=t0 is given by g(x,t0)=Asin(xa) . Write the wave equation for a general time t.
View SolutionThe equation of a wave travelling on a string stretched along the X-axis is given by
y=Ae(−xa+tT)2
(a) Write the dimensions of A, a and T.
(b) Find the wave speed.
(c) In which direction is the wave travelling?
(d) Where is the maximum of the pulse located at t=T and at t=2T?
View SolutionA wave is propagating along the length of a string taken as positive x-axis. The wave equation is given by y=Ae^((-t/t-x/A)^(2)) where A=5mm, T=1.0 s and lambda=8.0 cm (a) Find the velocity of the wave. (b) find the function f(t) represent the displacement of particle at x=0. (c ) Plot the function g(x) representing the shape of the string at t=0 (d) Plot the function g(x) of the string at t=0 and t=5 s
View Solutionएक लंबी तनी हुई डोरी पर एक तरंग धनात्मक -दिशा में चल रही है । इसका समीकरण है
y=y0e−(xλ−tT)2
जहाँ y0=4mm, T=1.0s तथा λ=4cm है । (a) तरंग की चाल बताएँ| (b) समय t के साथ x=0 के कण के विस्थपन के लिए फलन f(t) बताएँ । (c ) t=0 पर डोरी के विभिन्न कणों के विस्थापन के लिए फलन g(x) बताएँ । (d) t=0 पर डोरी की सकल बताने के लिए ग्राफ खींचे तथा (e) t = 5 s पर डोरी की शक्ल बताने के लिए ग्राफ खींचें ।
View SolutionA wave is propagating on a long stretched string along its length taken as positive x-axis the wave equation is given by y = y_(0) e^(-((t)/(T)-(x)/(lambda))^(2)),"where" y_(0) = 2 m m T = 1 . 0 sec and lambda = 6 cm find . Plot the shape of the string at t = 6 sec.
View SolutionA wave is propagating on a long stretched string along its length taken as positive x-axis the wave equation is given by
y=y0e−(tT−xλ)2,wherey0=2mm
T = 1 . 0 sec and λ=6cm find .
Plot the shape of the string at t = 6 sec.
View SolutionA wave propagates in a string in the positive x-direction with velocity v. The shape of the string at t=t_0 is given by f(x,t_0)=A sin ((x^2)/(a^2)) . Then the wave equation at any instant t is given by
View SolutionThe displacement of A particle at x = 0 of a stretched string carrying a wave in the positive X-direction is given by f(t)=Ae−t2. The wave speed is V. Write equation of the wave.
View SolutionA wave is propagating on a long stretched string along its length taken as the positive x-axis. The wave equation is given as
y=y0e−(tT−xλ)2
where y0=4mm,T=1.0sandλ=4cm.(a) find the velocity of wave. (b) find the function f(t) giving the displacement of particle at x=0. (c) find the function g(x) giving the shape of the string at t=0.(d) plot the shape g(x) of the string at t=0 (e) Plot of the shape of the string at t=5s.
View Solution

