A wave is propagating on a long stretched string along its length taken as the positive x-axis. The wave equation is given as
y=y0e−(tT−xλ)2
where y0=4mm,T=1.0sandλ=4cm.(a) find the velocity of wave. (b) find the function f(t) giving the displacement of particle at x=0. (c) find the function g(x) giving the shape of the string at t=0.(d) plot the shape g(x) of the string at t=0 (e) Plot of the shape of the string at t=5s.
(a) The wave equation may be written as y=y0e−1T2(tx(λ/T)2)
comparing with the general equation y=f(t−x/v), we see that
v=λT=4cm1.0s=4cm/s
(b)putting x=0 in the given equation,
f(t)=y0e−(t/T)2
(c ) putting t=0 in the given equation
g(x)=y0e−(x/λ)2
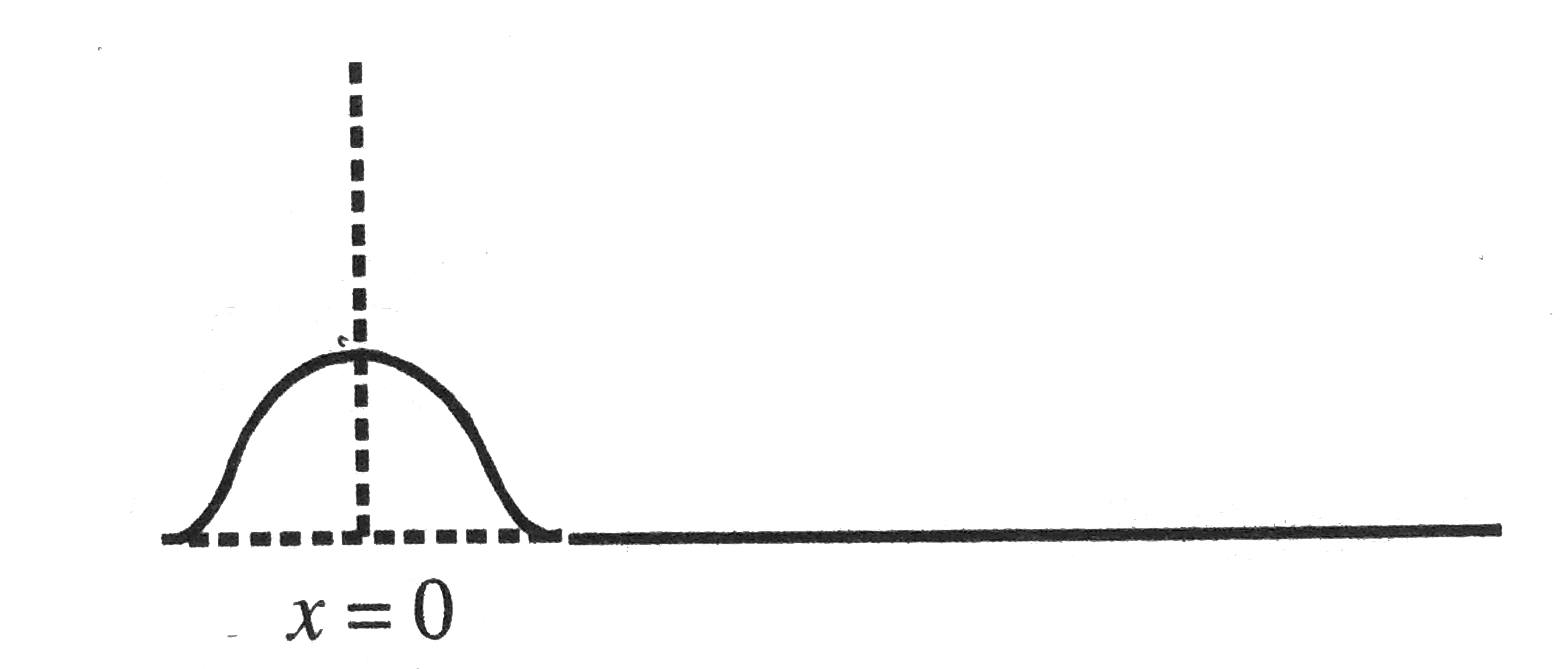

Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct
62 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct Answer
1 Video
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.2
23 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
The speed of a wave in a medium is 960ms−1. If 3600 waves are passing through a point in the medium in one minute then calculate the wavelength.
View SolutionThe figure shows three progressive waves A, B and c. wahat canbe concluded from the figure that with respect to wave A?
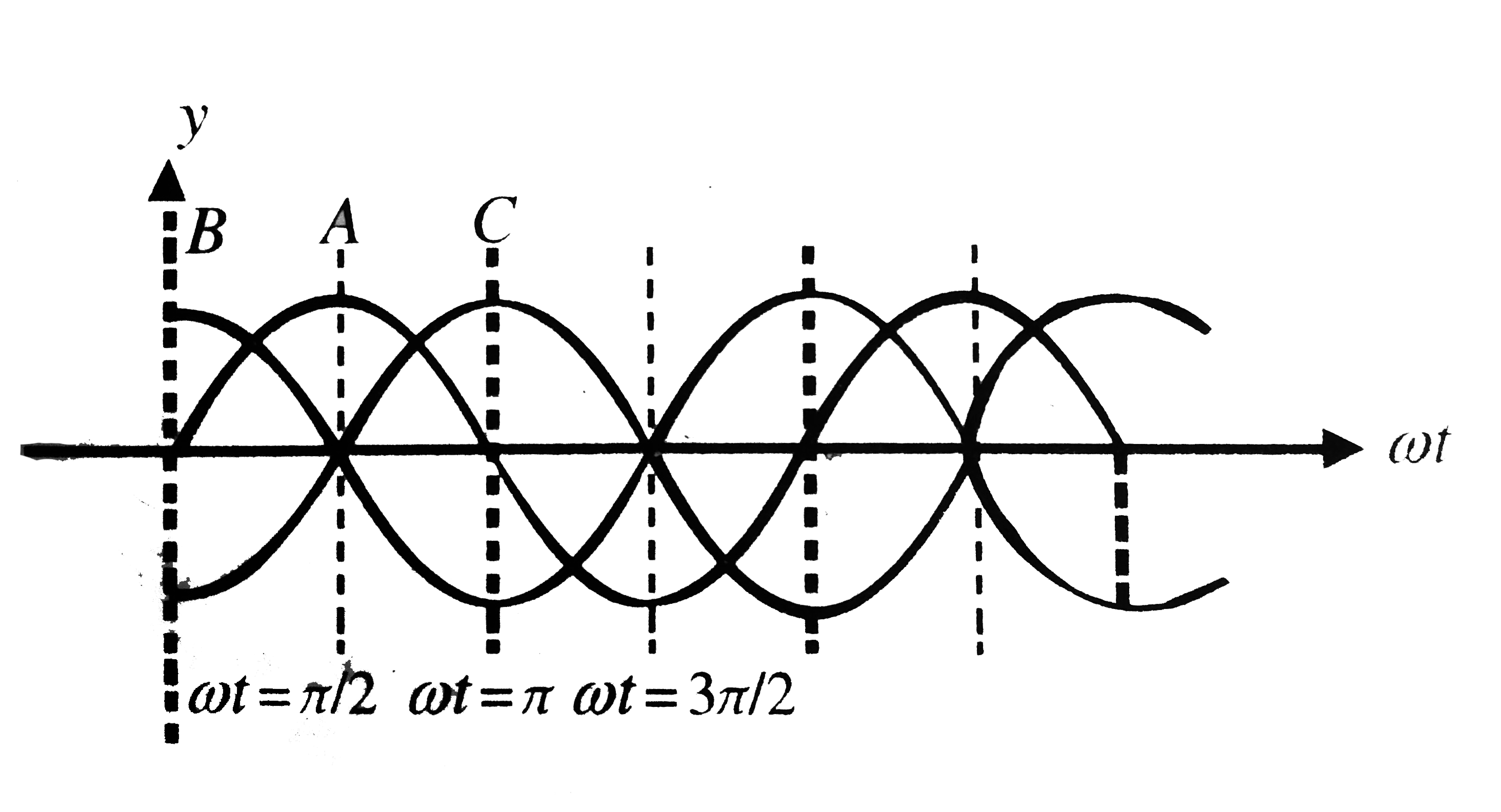
View SolutionA transverse wave is travelling along a string in the positive x-axis. The
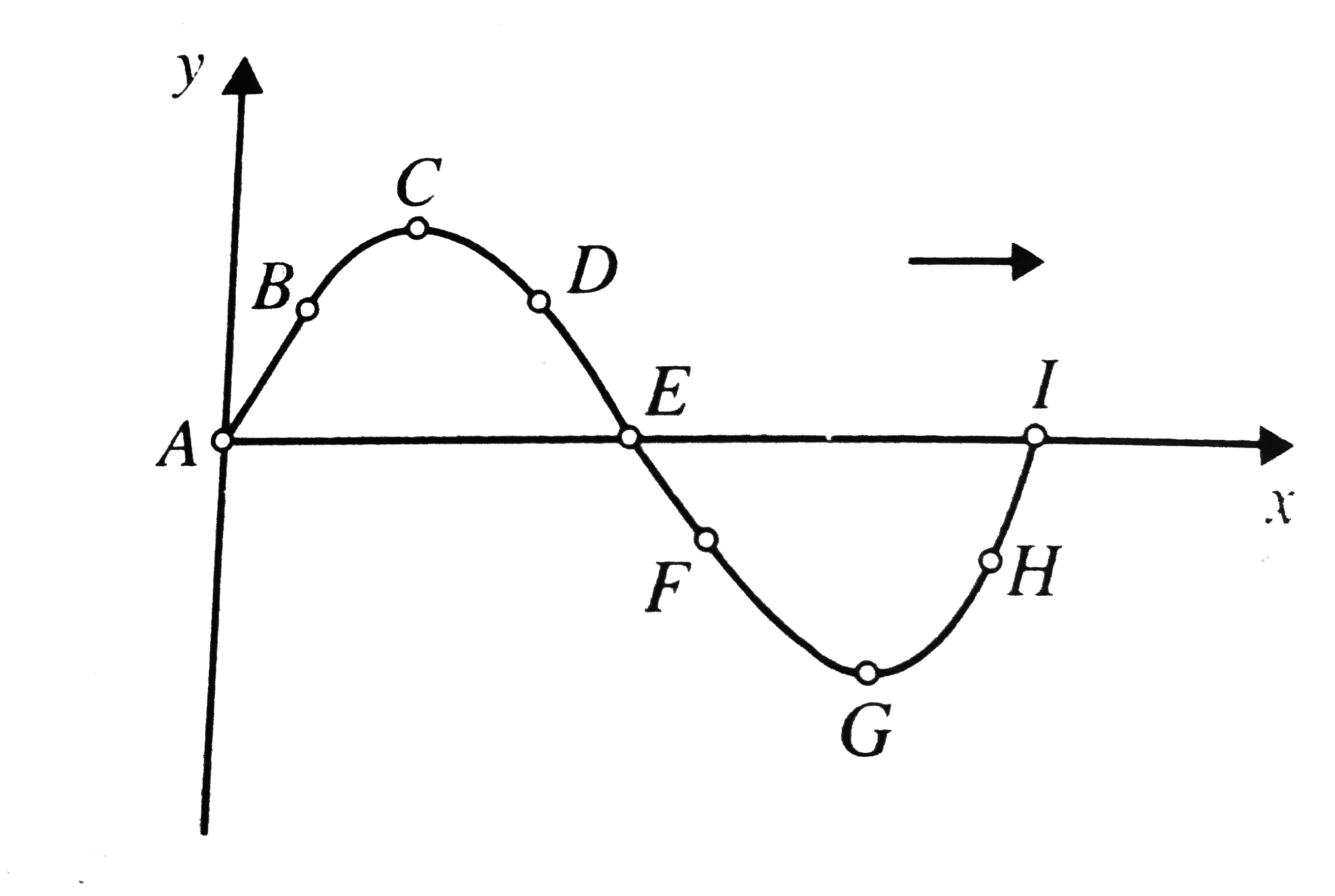
shows the photograph of the wave at an instant. Find
(a) the points moving upwards
(b) the points moving downwards
(c ) the points which have zero velocity
(d) the points which have maximum velocity
View SolutionConsider two hot bodies B1 and B2 which have temperature 100∘C and 80∘C respectively at t = 0. The temperature of surroundings is 40∘ C. The ratio of the respective rates of cooling R1 and R2 of these two bodies att=0 will be
View SolutionWhich of the following statements is/ are correct(Figure)
View SolutionA wave is propgting of a long stretched string along its length taken as the positive x-axis. The wave equation is given as
y=y0e−(tT−xλ)^2
where y0=4mm,T=1.0sandλ=4cm. d. Find the velocity of the particle t x=0. c. Find the function g(x) giving the shape of the string t t=0. d. Plot the shape g(x) of the string at t=0. e. Plot of the shape of the string at t=5s.
View SolutionThe displacement of the particle at x = 0 of a stretched string carrying a wave in the positive x-direction is given by f(t)sin(tT). The wave speed is v. Write the wave equation.
View SolutionA wave propagates on a string in the positive x-direction at a velocity u. The shape of the string at t=t0 is given by g(x,t0)=Asin(xa) . Write the wave equation for a general time t.
View SolutionThe equation of a wave travelling on a string stretched along the X-axis is given by
y=Ae(−xa+tT)2
(a) Write the dimensions of A, a and T.
(b) Find the wave speed.
(c) In which direction is the wave travelling?
(d) Where is the maximum of the pulse located at t=T and at t=2T?
View SolutionA wave is propagating along the length of a string taken as positive x-axis. The wave equation is given by y=Ae^((-t/t-x/A)^(2)) where A=5mm, T=1.0 s and lambda=8.0 cm (a) Find the velocity of the wave. (b) find the function f(t) represent the displacement of particle at x=0. (c ) Plot the function g(x) representing the shape of the string at t=0 (d) Plot the function g(x) of the string at t=0 and t=5 s
View Solutionएक लंबी तनी हुई डोरी पर एक तरंग धनात्मक -दिशा में चल रही है । इसका समीकरण है
y=y0e−(xλ−tT)2
जहाँ y0=4mm, T=1.0s तथा λ=4cm है । (a) तरंग की चाल बताएँ| (b) समय t के साथ x=0 के कण के विस्थपन के लिए फलन f(t) बताएँ । (c ) t=0 पर डोरी के विभिन्न कणों के विस्थापन के लिए फलन g(x) बताएँ । (d) t=0 पर डोरी की सकल बताने के लिए ग्राफ खींचे तथा (e) t = 5 s पर डोरी की शक्ल बताने के लिए ग्राफ खींचें ।
View SolutionA wave is propagating on a long stretched string along its length taken as positive x-axis the wave equation is given by y = y_(0) e^(-((t)/(T)-(x)/(lambda))^(2)),"where" y_(0) = 2 m m T = 1 . 0 sec and lambda = 6 cm find . Plot the shape of the string at t = 6 sec.
View SolutionA wave is propagating on a long stretched string along its length taken as positive x-axis the wave equation is given by
y=y0e−(tT−xλ)2,wherey0=2mm
T = 1 . 0 sec and λ=6cm find .
Plot the shape of the string at t = 6 sec.
View SolutionA wave propagates in a string in the positive x-direction with velocity v. The shape of the string at t=t_0 is given by f(x,t_0)=A sin ((x^2)/(a^2)) . Then the wave equation at any instant t is given by
View SolutionThe displacement of A particle at x = 0 of a stretched string carrying a wave in the positive X-direction is given by f(t)=Ae−t2. The wave speed is V. Write equation of the wave.
View SolutionA wave is propagating on a long stretched string along its length taken as the positive x-axis. The wave equation is given as
y=y0e−(tT−xλ)2
where y0=4mm,T=1.0sandλ=4cm.(a) find the velocity of wave. (b) find the function f(t) giving the displacement of particle at x=0. (c) find the function g(x) giving the shape of the string at t=0.(d) plot the shape g(x) of the string at t=0 (e) Plot of the shape of the string at t=5s.
View Solution

