A wedge is placed on the smooth surface of a fixed incline having inclination θ with the horizontal. The vertical wall of the wedge has height h and there is a small block A on the edge of the horizontal surface of the wedge. Mass of the wedge and the small block are M and m respectively.
(a) Find the acceleration of the wedge if friction between block A and the wedge is large enough to prevent slipping between the two.
(b) Find friction force between the block and the wedge in the above case. Also find the normal force between the two.
(c) Assuming there is no friction between the block and the wedge, calculate the time in which the block will hit the incline.
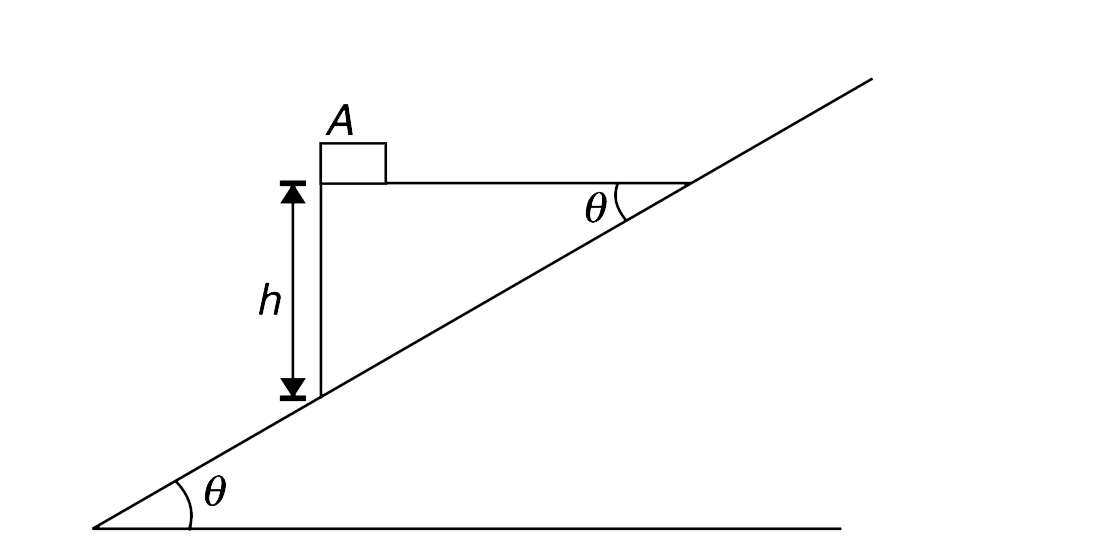
The correct Answer is:(a) gsinθ
(b) f=12mgsin2θ
N=mgcos2θ
(c) t=
⎷(2hM+msin2θ(M+m)gsin2θ)
Step by step video, text & image solution for A wedge is placed on the smooth surface of a fixed incline having inclination theta with the horizontal. The vertical wall of the wedge has height h and there is a small block A on the edge of the horizontal surface of the wedge. Mass of the wedge and the small block are M and m respectively. (a) Find the acceleration of the wedge if friction between block A and the wedge is large enough to prevent slipping between the two. (b) Find friction force between the block and the wedge in the above case. Also find the normal force between the two. (c) Assuming there is no friction between the block and the wedge, calculate the time in which the block will hit the incline. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
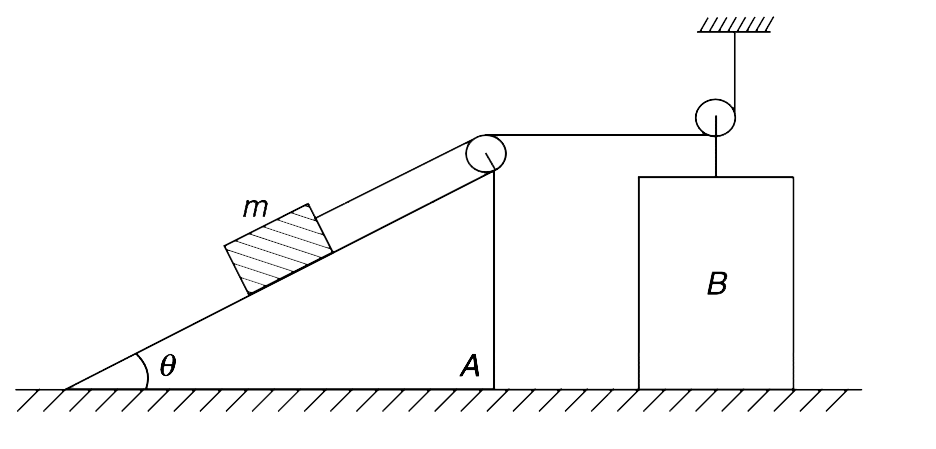
In the system shown in the figure all surfaces are smooth and both the pulleys are mass less. Block on the incline surface of wedge A has mass m. Mass of A and B are M = 4 m and M0=2 m respectively. Find the acceleration of wedge A when the system is released from rest.
View SolutionIn the Fig. shown, mass 'm' is being pulled on the incline of a wedge of mass M. All the surface are smooth. Find the acceleration of the wedge.
View Solution
Knowledge Check
In the figure if block A and wedge b will move with same acceleration, then the magnitude of normal reaction between the block and the wedge will be (There is no friction between block and the wedge and the wedge moves on horizontal surface as shown.)
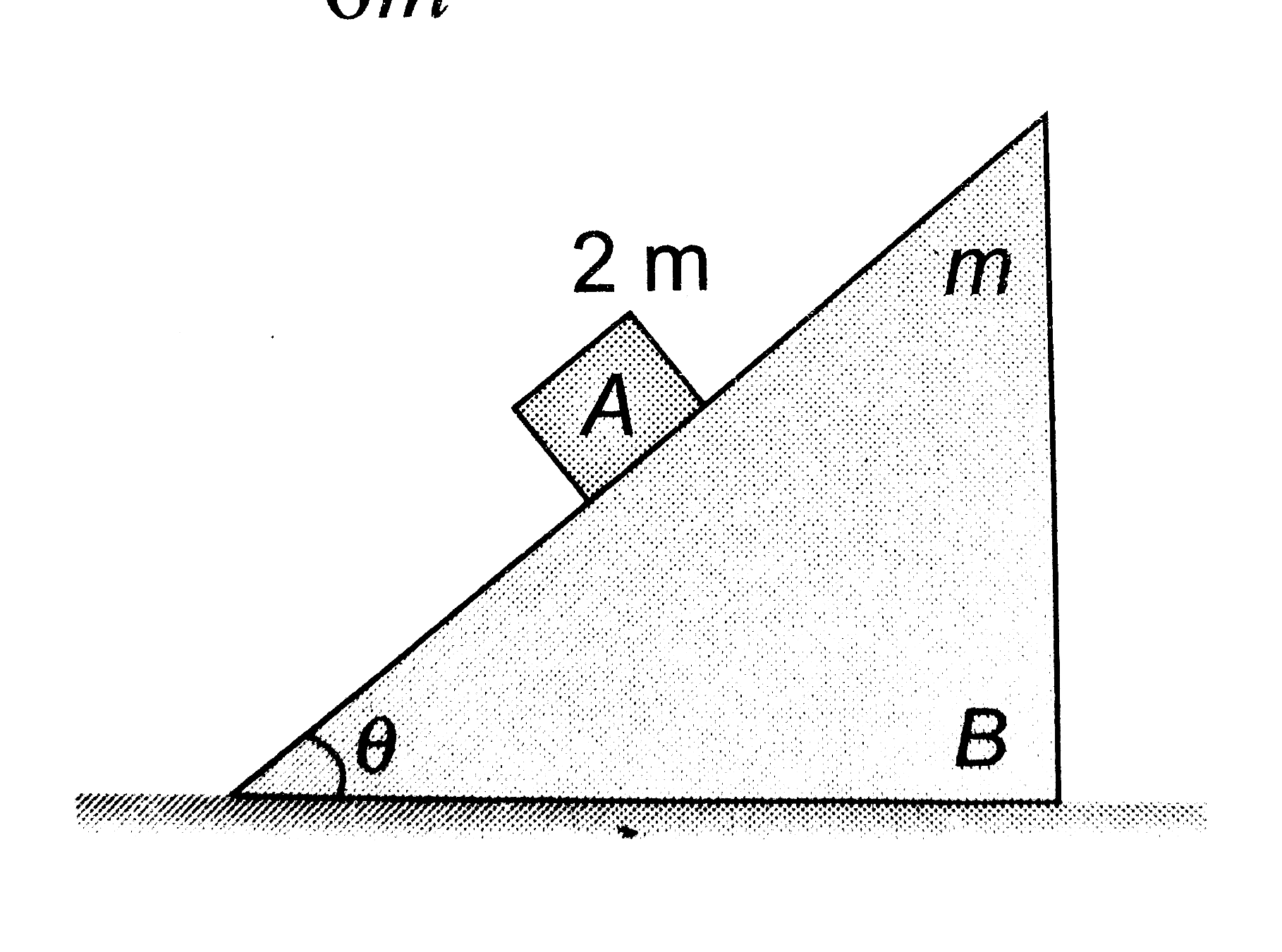 A2mg/coshtηB2mgcoshtηCmgcoshtηDnone of these
A2mg/coshtηB2mgcoshtηCmgcoshtηDnone of theseIn fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.
 Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θ
Aa=F(1−cosθ)mg2sinθcosθM+2msin2θBa=F(1+cosθ)+mgsinθcosθM+msin2θCa=F(1−cosθ)−mgsinθcosθM+msin2θDa=F(1+cosθ)−mgsinθcosθM−msin2θ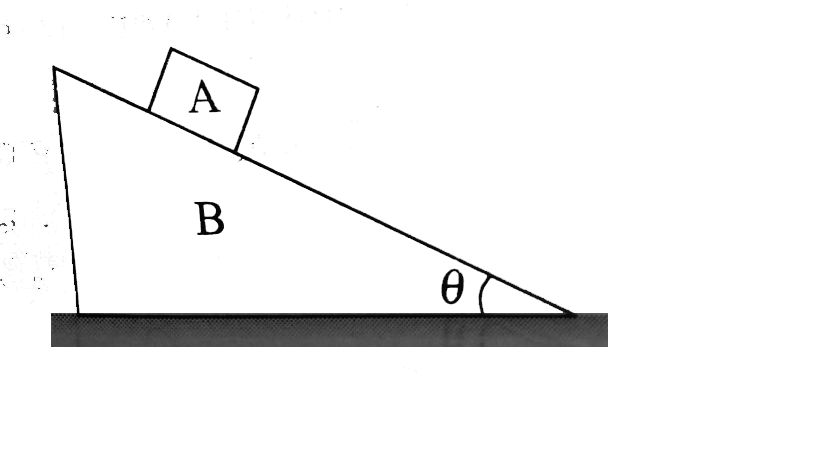
A block is placed on a smooth wedge of inclination angle θ with the horizontal. What minimum acceleration should be given to the wedge in the horizontal direction so that the block starts moving up along the incline?A>gcotθB>>anθC>gsinθD>gcosθ
The coefficient of friction between the block A of mass m and the triangular wedge B of mass M is μ. There in no friction between the wedge and the plane if the system (block A+ wedge B) is released so that there is no stiding between A and B find the inclination θ

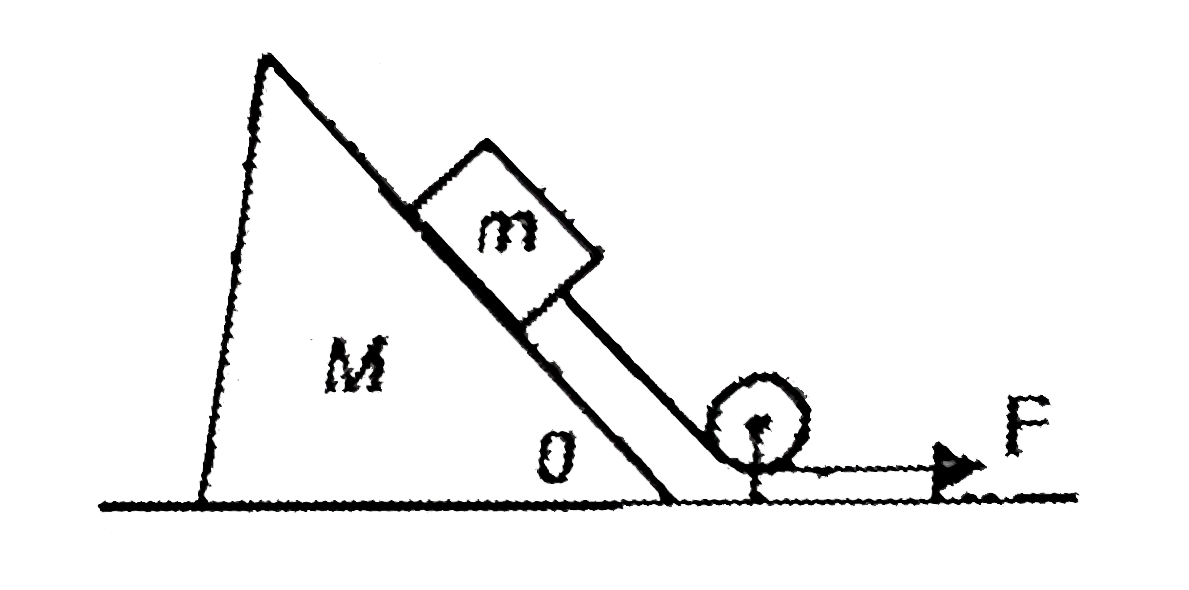
View SolutionA wedge of mass M makes an angle θ with the horizontal. The wedge is placed on horizontal frictionless surface. A small block of mass m is placed on the inclined surface of wedge. What horizontal force F must be applied to the wedge so that the force of friction between the block and wedge is zero ?
View SolutionA block of mass m is placed on a smooth wedge of inclination. The whole system is accelerated horizontally so that block does not slip on the wedge Find the i) Acceleration of the wedge Force to be applied on the wedge Force exerted by the wedge on the block .
View Solutiona Block of mass m is placed on a wedge of mass M there is no friction between the block and the wedge .The minmum coefficient of friction between the wedge and the gound so that wedge does not move is,
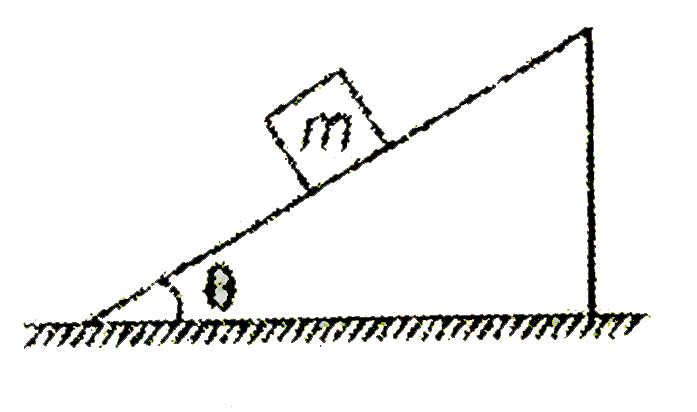
View SolutionIn the system shown block is released from rest on the inclined surface of the wedge. The acceleration of the wedge will be (assume friction to be absent)
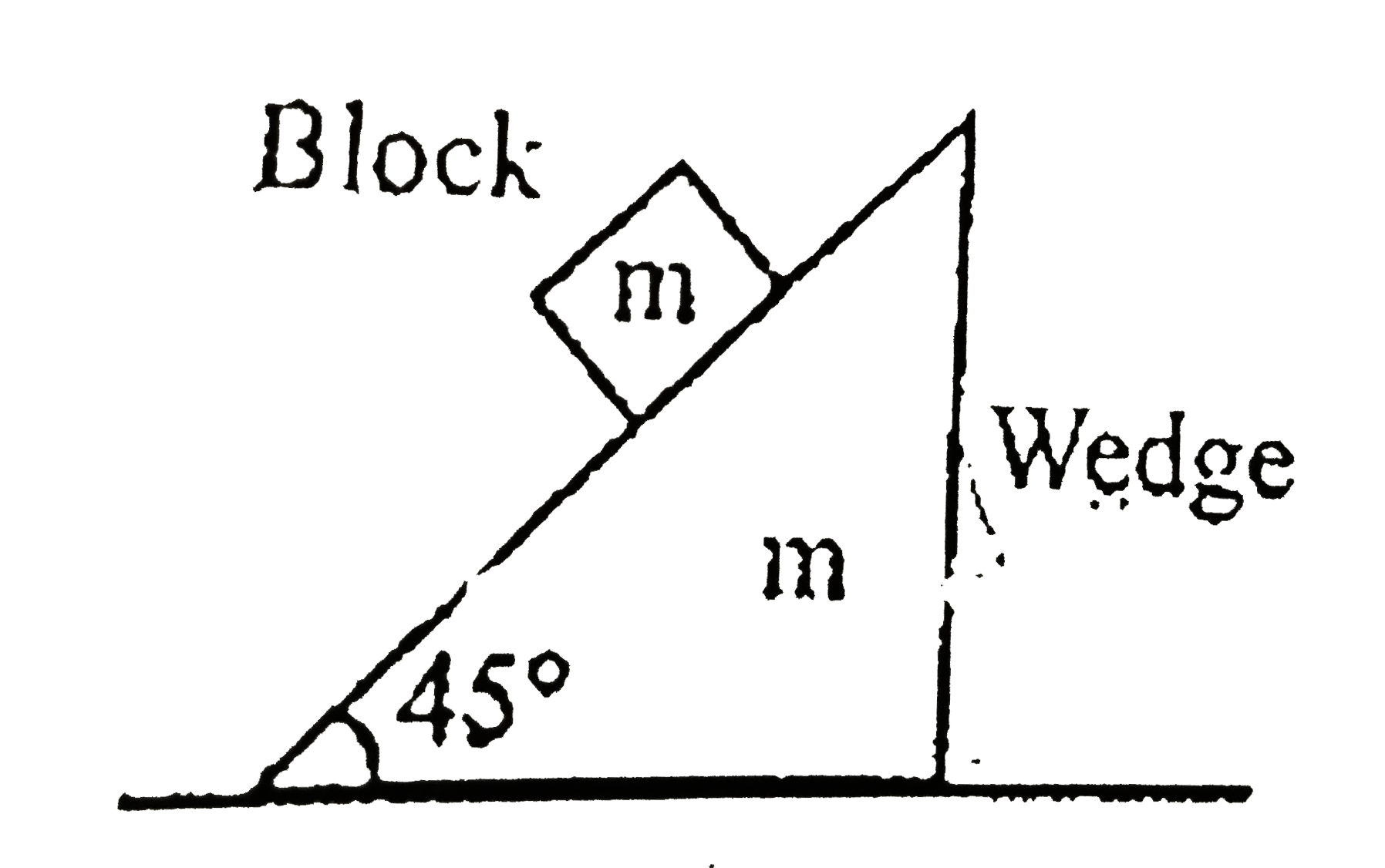
View Solution
