A wire along the x-axis carries a current of 3.50A in the negative direction. Calculate the force (expressed in term of unit vectors) on a 1.00cm sectioin of the wire exerted by these magnetic fiels.
a. B=−(0.65T)ˆjb.B=+(0.56T)hatk c. B=−(0.31T)ˆj
d. B=0.33Tˆi−(0.28t)ˆk e. B=+(0.74T)ˆj−0(0.36T)ˆk
To solve the problem of calculating the force on a wire carrying a current in the presence of a magnetic field, we can follow these steps:
1. Identify the Given Values:
- Current, I=3.50A (in the negative x-direction)
- Length of the wire section, L=1.00cm=0.01m
- Direction of the current: −^i
2. Use the Formula for Magnetic Force:
The force →F on a current-carrying wire in a magnetic field is given by:
→F=I→L×→B
where →L is the length vector of the wire and →B is the magnetic field vector.
3. Calculate the Force for Each Magnetic Field Option:
We will compute the force for each magnetic field option provided.
Option A: →B=−0.65^j
→F=3.50×0.01(−^i)×(−0.65^j)
=0.035^i×(−0.65^j)=0.02275^k
Option B: →B=0.56^k
→F=3.50×0.01(−^i)×(0.56^k)
=−0.035^i×0.56^k=−0.0196^j
Option C: →B=−0.31^j
→F=3.50×0.01(−^i)×(−0.31^j)
=0.035^i×0.31^j=0.01085^k
Option D: →B=0.33^i−0.28^k
→F=3.50×0.01(−^i)×(0.33^i−0.28^k)
The ^i×^i component is zero, so:
=3.50×0.01×(−0.28^k)=0.0098^j
Option E: →B=0.74^j−0.36^k
→F=3.50×0.01(−^i)×(0.74^j−0.36^k)
=3.50×0.01×(−0.74^i×^j+0.36^i×^k)
=0.0259^k+0.0126^j
4. Summarize Results:
- Option A: →F=0.02275^k
- Option B: →F=−0.0196^j
- Option C: →F=0.01085^k
- Option D: →F=0.0098^j
- Option E: →F=0.0259^k+0.0126^j
- Current, I=3.50A (in the negative x-direction)
- Length of the wire section, L=1.00cm=0.01m
- Direction of the current: −^i
The force →F on a current-carrying wire in a magnetic field is given by:
→F=I→L×→B
where →L is the length vector of the wire and →B is the magnetic field vector.
We will compute the force for each magnetic field option provided.
→F=3.50×0.01(−^i)×(−0.65^j)
=0.035^i×(−0.65^j)=0.02275^k
→F=3.50×0.01(−^i)×(0.56^k)
=−0.035^i×0.56^k=−0.0196^j
→F=3.50×0.01(−^i)×(−0.31^j)
=0.035^i×0.31^j=0.01085^k
→F=3.50×0.01(−^i)×(0.33^i−0.28^k)
The ^i×^i component is zero, so:
=3.50×0.01×(−0.28^k)=0.0098^j
→F=3.50×0.01(−^i)×(0.74^j−0.36^k)
=3.50×0.01×(−0.74^i×^j+0.36^i×^k)
=0.0259^k+0.0126^j
- Option A: →F=0.02275^k
- Option B: →F=−0.0196^j
- Option C: →F=0.01085^k
- Option D: →F=0.0098^j
- Option E: →F=0.0259^k+0.0126^j
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - INTRODUCTORY EXERCISE
1 Video
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Video
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Video
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Video
Similar Questions
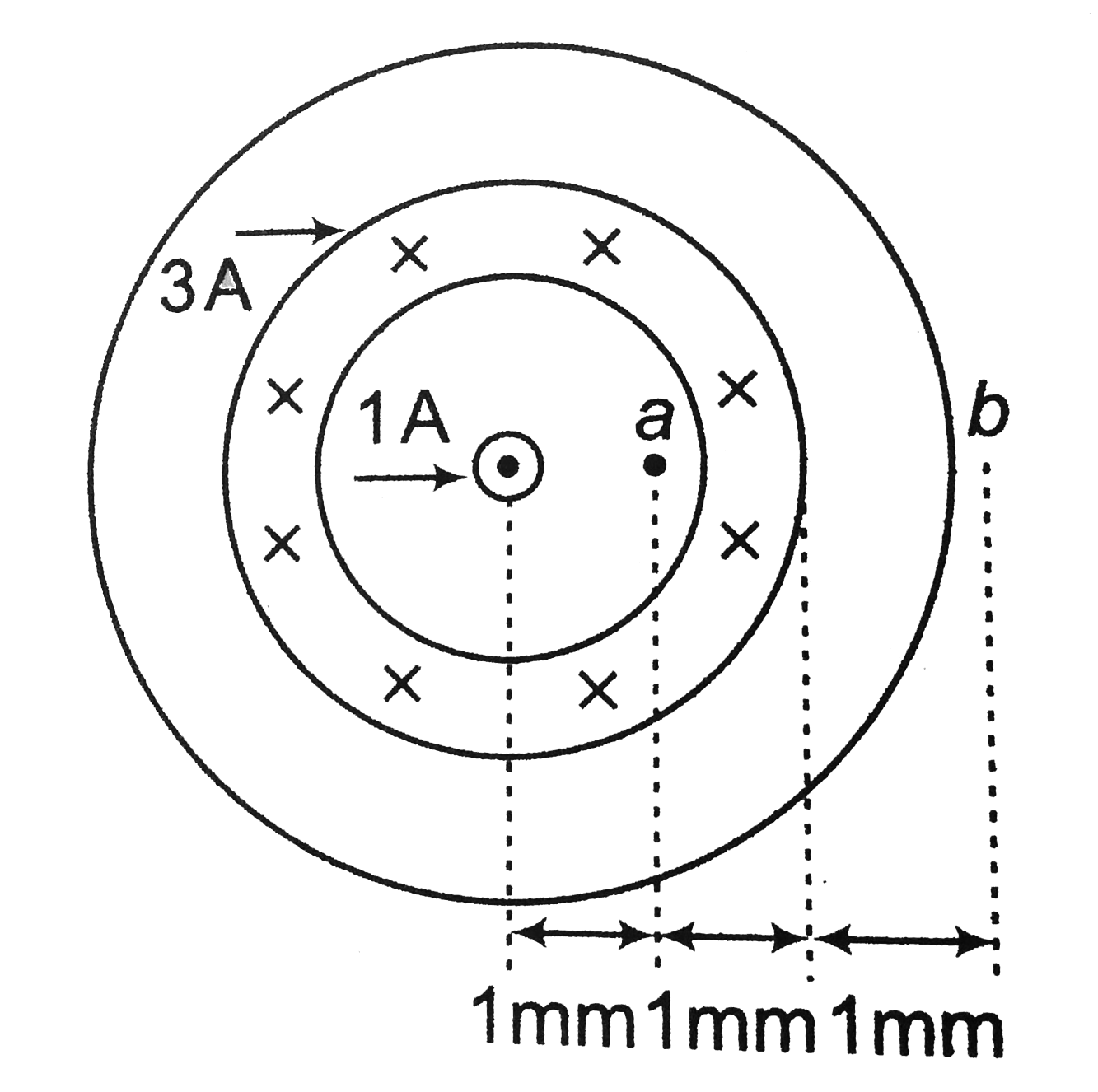
Figure given in the question is a cross-sectional view of a coaxial cable. The centre conductor. surrounded by a rubber layer, which is surrounded by an outer conductor, which is surround by another rubber layer. The current in the inner conductor is 1.0A out of the page, and the current in the outer conductor is 3.0 A into the page. Determine the magnitude and direction of the magnetic field at points a and b.
View SolutionIn the Bohr model of the hydrogen atom, in the lowest energy state the electron revolves round the proton at a speed of 2.2×106ms in a circular orbit of radius 5.3×10−11 m.
(a) What is the orbital period of the electron?
(b) If the orbiting electron is considered to be a current loop, what is the current I? (c) What is the magnetic moment of the atom due to the motion of the electron?
View SolutionTwo circular coils of radii 5cm and 10cm carry currents of 2A. The coils have 50 and 100 turns respectiely and are placed in such a way that their planes as well as their cetre coincide. Magnitude of magnetic field at the common centre of coils is
View SolutionA long wire carries a steady curent . It is bent into a circle of one turn and the magnetic field at the centre of the coil is B. It is then bent into a circular loop of n turns. The magnetic field at the centre of the coil will be
View SolutionA bar magnet is hung by a thin cotton thread in a uniform horizontal magnetic field and is in equilibrium state. The energy required to rotate it by 60 is W. Now the torque required to keep the magnet in this new position is
View SolutionVectors perpendicular toˆi−ˆj−ˆk and in the plane of ˆi+ˆj+ˆkand−ˆi+ˆj+ˆk are (A) ˆi+ˆk (B) 2ˆi+ˆj+ˆk (C) 3ˆi+2ˆj+ˆk (D) −4ˆi−2ˆj−2ˆk
View SolutionThe vectors which is/are coplanar with vectors ˆi+ˆj+2ˆkandˆi+2ˆj+ˆk and perpendicular to the vector ˆi+ˆj+ˆk is /are (A) ˆj−ˆk (B) −ˆi+ˆj (C) ˆi−ˆj (D) −ˆj+ˆk
View SolutionA wire along the x-axis carries a current of 3.50A in the negative direction. Calculate the force (expressed in term of unit vectors) on a 1.00cm sectioin of the wire exerted by these magnetic fiels.
a. B=−(0.65T)ˆjb.B=+(0.56T)hatk c. B=−(0.31T)ˆj
d. B=0.33Tˆi−(0.28t)ˆk e. B=+(0.74T)ˆj−0(0.36T)ˆk
View SolutionThree vectors a=ˆi+ˆj−ˆk,b=−ˆi+2ˆj+ˆkandc=−ˆi+2ˆj−ˆk, then the unit vector perpendicular to both a+b and b+c is
View SolutionIf a=ˆi+ˆj+ˆk,b=ˆi+ˆj−ˆk, then vectors perpendicular to a and b is/are
View SolutionIf a=ˆi+ˆj+ˆkandb=ˆi−ˆj, then vectors (a⋅ˆi+ˆi+(a⋅ˆj+(a⋅ˆk)ˆk,(b⋅ˆi)ˆi+(bˆj)ˆj+(b⋅ˆk)ˆkandˆi+ˆj−2ˆk
View SolutionThree vectors a=ˆi+ˆj−ˆk,b=−ˆi+2ˆj+ˆkandc=−ˆi+2ˆj−ˆk, then the unit vector perpendicular to both a+b and b+c is
View SolutionVectors perpendicular toˆi−ˆj−ˆk and in the plane of ˆi+ˆj+ˆkand−ˆi+ˆj+ˆk are (A) ˆi+ˆk (B) 2ˆi+ˆj+ˆk (C) 3ˆi+2ˆj+ˆk (D) −4ˆi−2ˆj−2ˆk
View SolutionThe vectors which is/are coplanar with vectors ˆi+ˆj+2ˆkandˆi+2ˆj+ˆk and perpendicular to the vector ˆi+ˆj+ˆk is /are (A) ˆj−ˆk (B) −ˆi+ˆj (C) ˆi−ˆj (D) −ˆj+ˆk
View SolutionIf a=ˆi+ˆj+ˆk,b=ˆi+ˆj−ˆk, then vectors perpendicular to a and b is/are
View Solution

